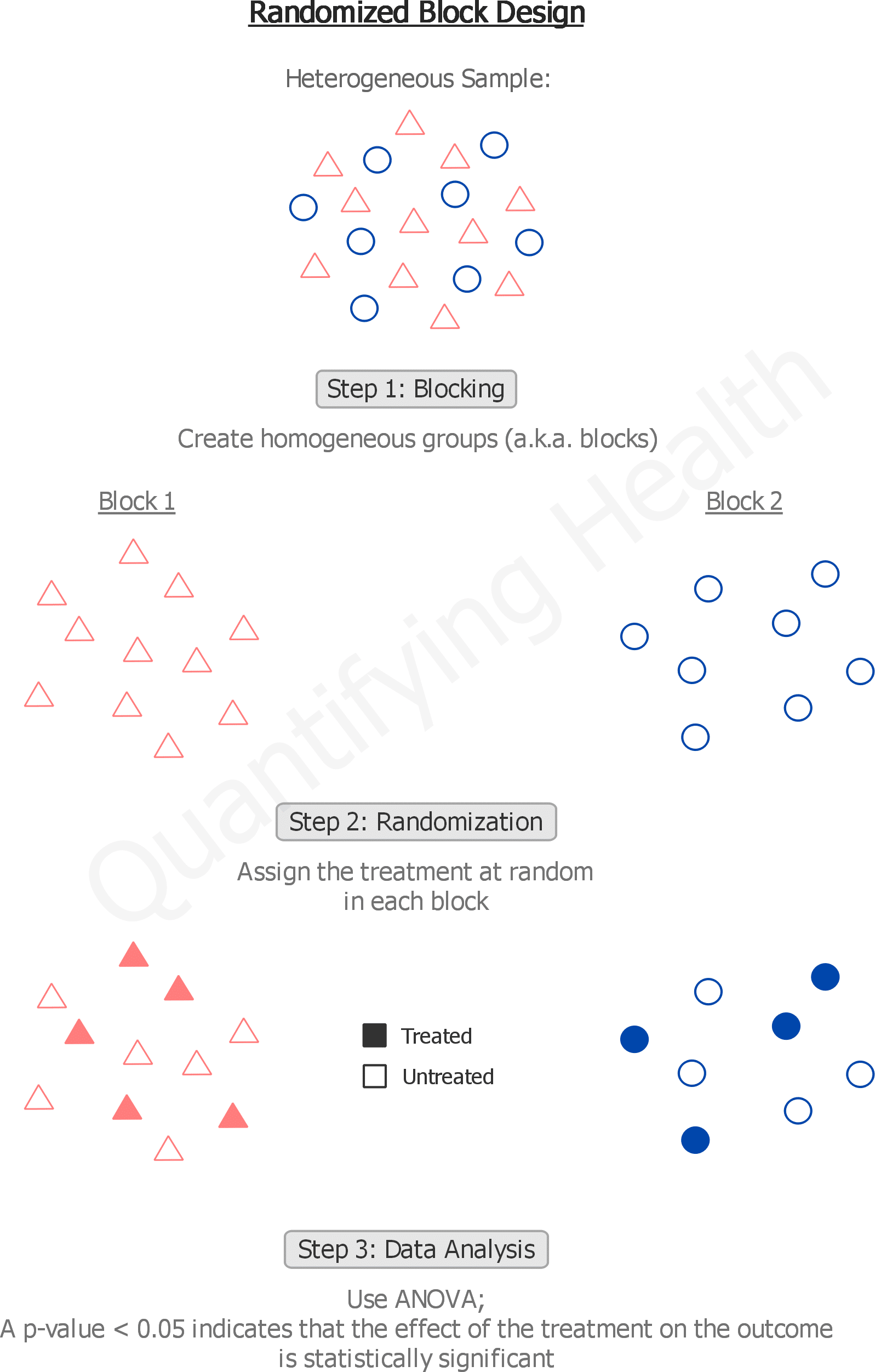
Randomized Block Design: An Introduction
A randomized block design is a type of experiment where participants who share certain characteristics are grouped together to form blocks , and then the treatment (or intervention) gets randomly assigned within each block.
The objective of the randomized block design is to form groups where participants are similar, and therefore can be compared with each other.

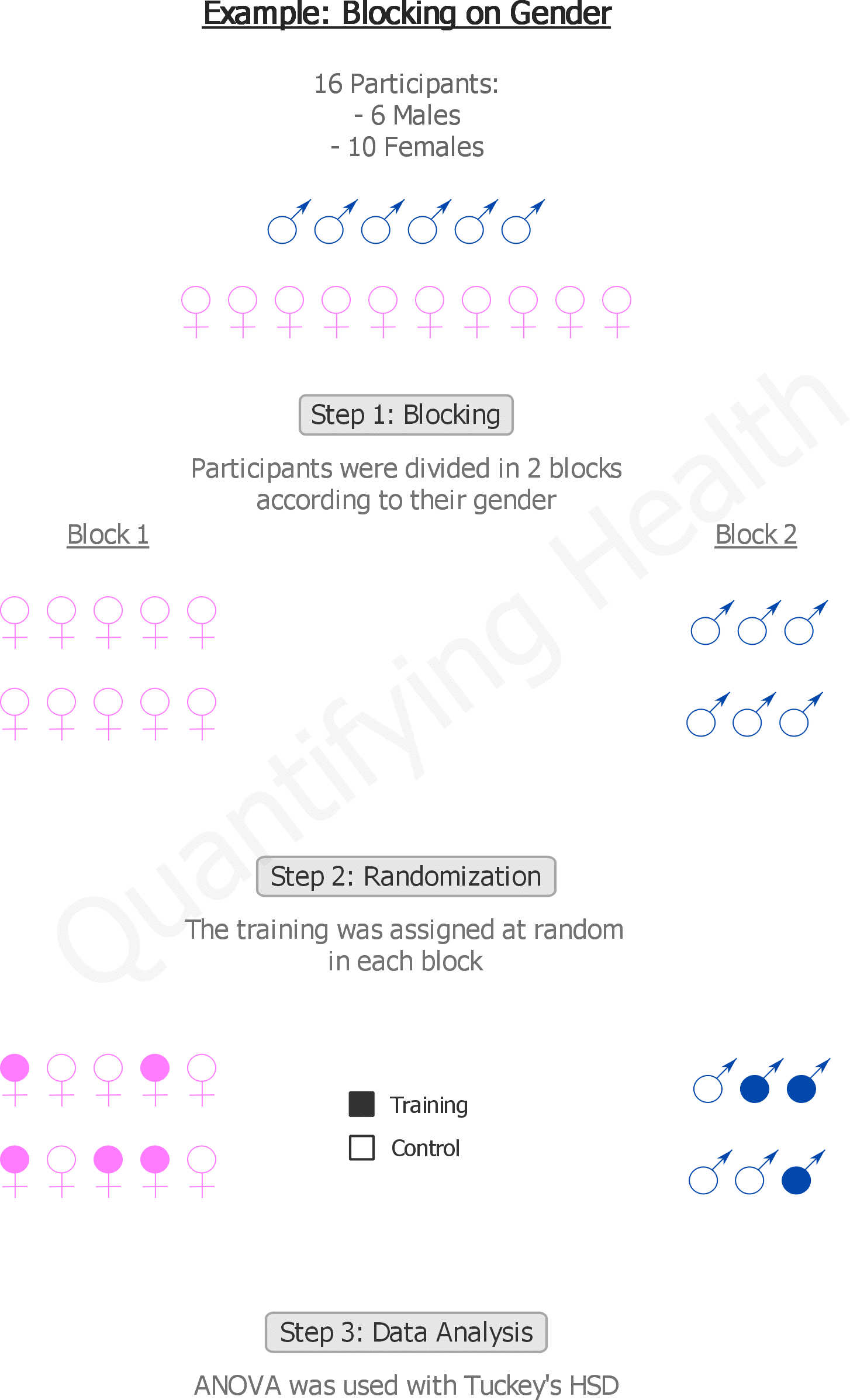
An Example: Blocking on gender
Santana-Sosa et al. set to study the effect of a 12-week physical training program on the ability to perform daily activities in Alzheimer’s disease patients.
And because physical capability differs substantially between males and females, the authors decided to block on gender.
Why gender?
Because gender satisfies the following 2 conditions:
- It will certainly affect the test measurements (i.e. the outcome)
- It is not an interesting variable in itself to be studied (as it is better to study variables that CAN be manipulated by patients in order to improve their physical ability)
Therefore, it would be very useful to block on gender in order to remove its effect as an alternative explanation of the outcome.
16 patients participated in the study: 10 females and 6 males.
The blocks were created as follows:
When to use a randomized block design?
Use a randomized block design if:
- An unwanted/uninteresting variable affects the outcome.
- This variable can be measured.
- Your sample size is not large enough for simple randomization to produce equal groups (see Randomized Block Design vs Completely Randomized Design ).
What happens if you don’t block?
If you don’t block, all the variability associated with the blocks end up in the error term which makes it hard to detect an effect when in fact there is one.
So if you don’t block, you will reduce the statistical power of the study.
In other words, when the error term is inflated, the percentage of variability explained by the statistical model diminishes. Therefore, the model becomes a less accurate representation of reality.
BOTTOM LINE:
Blocking reduces the error term, making your statistical model more predictive and more generalizable.
Limitations of the randomized block design
Here are some of the limitations of the randomized block design and how to deal with them:
1. We cannot block on too many variables
As the number of blocking variables increases, the number of blocks created increases, approaching the sample size — i.e. the number of participants in each block would be very low, creating a problem for the randomized block design.
2. Difficulty in choosing the number of blocks
Since the number of blocks is the number of categories of the blocking variable, choosing a blocking variable that does not have too much or too few categories will be important because:
- If you used fewer blocks than you need: You may have a hard time maintaining homogeneity within each block.
- If you used more blocks than your sample size allows: You may end up with few participants in each block to be properly randomized to treatment options.
When in doubt, decide on the number of blocks based on previous literature.
3. Difficulty in detecting/measuring the blocking variable
We will divide this section into 3 categories [ Source: Design and Analysis of Experiments ]:
- When the blocking variable is known and controllable : Solution: Use a randomized block design.
- When the blocking variable is known but uncontrollable : Solution: Try to adjust for it in the statistical analysis.
- When the blocking variable is unknown : Solution: Use simple randomization in the hope that it will produce equal and comparable study groups.
- Lewis-Beck M, Bryman A, Liao T. The SAGE Encyclopedia of Social Science Research Methods .; 2004. doi:10.4135/9781412950589
- Lawson J. Design and Analysis of Experiments with R . 1 edition. Chapman and Hall/CRC; 2014.
- Design of Experiments . Coursera. Accessed August 18, 2020.

Further reading
- Matched Pairs Design
- Posttest-Only Control Group Design
- Pretest-Posttest Control Group Design
- Experimental vs Quasi-Experimental Design
Teach yourself statistics
Randomized Block Designs
This lesson begins our discussion of randomized block experiments . The purpose of this lesson is to provide background knowledge that can help you decide whether a randomized block design is the right design for your study. Specifically, we will answer four questions:
- What is a blocking variable?
- What is blocking?
- What is a randomized block experiment?
- What are advantages and disadvantages of a randomized block experiment?
We will explain how to analyze data from a randomized block experiment in the next lesson: Randomized Block Experiments: Data Analysis .
Note: The discussion in this lesson is confined to randomized block designs with independent groups . Randomized block designs with repeated measures involve some special issues, so we will discuss the repeated measures design in a future lesson.
What is a Blocking Variable?
In a randomized block experiment, a good blocking variable has four distinguishing characteristics:
- It is included as a factor in the experiment.
- It is not of primary interest to the experimenter.
- It affects the dependent variable.
- It is unrelated to independent variables in the experiment.
A blocking variable is a potential nuisance variable - a source of undesired variation in the dependent variable. By explicitly including a blocking variable in an experiment, the experimenter can tease out nuisance effects and more clearly test treatment effects of interest.
Warning: If a blocking variable does not affect the dependent variable or if it is strongly related to an independent variable, a randomized block design may not be the best choice. Other designs may be more efficient.
What is Blocking?
Blocking is the technique used in a randomized block experiment to sort experimental units into homogeneous groups, called blocks . The goal of blocking is to create blocks such that dependent variable scores are more similar within blocks than across blocks.
For example, consider an experiment designed to test the effect of different teaching methods on academic performance. In this experiment, IQ is a potential nuisance variable. That is, even though the experimenter is primarily interested in the effect of teaching methods, academic performance will also be affected by student IQ.
To control for the unwanted effects of IQ, we might include IQ as a blocking variable in a randomized block experiment. We would assign students to blocks, such that students within the same block have the same (or similar) IQ's. By holding IQ constant within blocks, we can attribute within-block differences in academic performance to differences in teaching methods, rather than to differences in IQ.
What is a Randomized Block Experiment?
A randomized block experiment with independent groups is distinguished by the following attributes:
- The design has one or more factors (i.e., one or more independent variables ), each with two or more levels .
- Treatment groups are defined by a unique combination of non-overlapping factor levels.
- Experimental units are randomly selected from a known population .
- Each experimental unit is assigned to one block, such that variability within blocks is less than variability between blocks.
- The number of experimental units within each block is equal to the number of treatment groups.
- Within each block, each experimental unit is randomly assigned to a different treatment group.
- Each experimental unit provides one dependent variable score.
The table below shows the layout for a typical randomized block experiment.
In this experiment, there are five blocks ( B i ) and four treatment levels ( T j ). Dependent variable scores are represented by X i, j , where X i, j is the score for the subject in block i who received treatment j .
Advantages and Disadvantages
With respect to analysis of variance, a randomized block experiment with independent groups has advantages and disadvantages. Advantages include the following:
- With an effective blocking variable - a blocking variable that is strongly related to the dependent variable but not related to the independent variable(s) - the design can provide more precision than other independent groups designs of comparable size.
- The design works with any number of treatments and blocking variables.
Disadvantages include the following:
- When the experiment has many treatment levels, it can be hard to form homogeneous blocks.
- With an ineffective blocking variable - a blocking variable that is weakly related to the dependent variable or strongly related to one or more independent variables - the design may provide less precision than other independent groups designs of comparable size.
- The design assumes zero interaction between blocks and treatments. If an interaction exists, tests of treatment effects may be biased.
Test Your Understanding
Which, if any, of the following attributes does not describe a good blocking variable?
(A) It is included as a factor in the experiment. (B) It is not of primary interest to the experimenter. (C) It affects the dependent variable. (D) It affects the independent variable. (E) All of the attributes describe a good blocking variable.
The correct answer is (D).
A good blocking variable is not related to an independent variable. When the blocking variable and treatment variable are related, tests of treatment effects may be biased.
Why would an experimenter choose to use a randomized block design?
(A) To test the effect of a blocking variable on a dependent variable. (B) To assess the interaction between a blocking variable and an independent variable. (C) To control unwanted effects of a suspected nuisance variable. (D) None of the above. (E) All of the above.
The correct answer is (C).
The blocking variable is not of primary interest to an experimenter, so the experimenter would not choose a randomized block design to test the effect of a blocking variable. A randomized block design assumes that there is no interaction between a blocking variable and an independent variable, so the experimenter would not choose a randomized block design to test the interaction effect. A full factorial experiment would be a better choice to accomplish either of these objectives.
A blocking variable is a potential nuisance variable - a source of undesired variation in the dependent variable. By explicitly including a blocking variable in an experiment, the experimenter can tease out nuisance effects and more clearly test treatment effects of interest. Thus, an experimenter might choose a randomized block design to control unwanted effects of a suspected nuisance variable.

IMAGES
VIDEO