probability assignment questions

Browse Course Material

Course info, instructors.

• Dr. Jeremy Orloff
• Dr. Jennifer French Kamrin

Departments

• Mathematics

As Taught In

• Discrete Mathematics
• Probability and Statistics

Learning Resource Types

Introduction to probability and statistics, problem sets with solutions.

You are leaving MIT OpenCourseWare

• Number System and Arithmetic
• Probability
• Mensuration
• Trigonometry
• Mathematics

Practice Problems on Probability (Easy)

Probability is an important chapter for the students of Class 9, 10, 11, and 12. The Probability Questions, with their answers included in this article, will help you understand the basic concepts and formulas through a number of solved and unsolved questions. These questions cover concepts like Sample Space, Events, Coin Probability, etc. Solving these problems will improve your understanding and problem-solving skills in probability.

Important Formulas on Probability

Solved practice problems on probability (easy).

Question 1: There are 8 balls in a container, 4 are red, 1 is yellow and 3 are blue. What is the probability of picking a yellow ball?

Probability of picking a ball

Probability is equal to the number of yellow balls in the container divided by the total number of balls in the container, i.e. 1/8. 

Question 2:   A dice is rolled. What is the probability that an even number has been obtained?

Probability of Rolling a Dice

When fair six-sided dice are rolled, there are six possible outcomes: 1, 2, 3, 4, 5, or 6. Out of these, half are even (2, 4, 6) and half are odd (1, 3, 5). Therefore, the probability of getting an even number is: P(even) = number of even outcomes / total number of outcomes  P(even) = 3 / 6 P(even) = 1/2

Question 3: A fair six-sided die is rolled. What is the probability of rolling a number greater than 4?

There are 2 favorable outcomes (5 and 6) out of 6 possible outcomes. Probability = Number of favorable outcomes / Total number of outcomes. = 2 / 6 = 1 / 3 ≈ 0.3333 or 33.33%.

Question 4: A jar contains 3 red, 4 blue, and 5 green marbles. What is the probability of randomly drawing a red marble?

Total marbles = 3 (red) + 4 (blue) + 5 (green) = 12. Probability of drawing a red marble = Number of red marbles / Total number of marbles. = 3 / 12 = 1 / 4 = 0.25 or 25%.

Question 5: From a deck of 52 cards, what is the probability of drawing an ace or a king?

There are 4 aces and 4 kings in the deck. Total favorable outcomes = 4 (aces) + 4 (kings) = 8. Probability = Number of favorable outcomes / Total number of outcomes. = 8 / 52 = 2 / 13 ≈ 0.1538 or 15.38%.

Question 6: What is the probability of getting an even number when a fair six-sided die is rolled?

There are 3 even numbers on a die (2, 4, 6). Total outcomes = 6. Probability of rolling an even number = Number of even numbers / Total outcomes. = 3 / 6 = 1 / 2 = 0.5 or 50%.

Question 7: In a class of 20 students, 12 are girls. What is the probability of randomly selecting a boy?

Total students = 20. Number of boys = Total students - Number of girls = 20 - 12 = 8. Probability of selecting a boy = Number of boys / Total students. = 8 / 20 = 2 / 5 = 0.4 or 40%.

Question 8: A spinner with numbers 1 to 5 is spun once. What is the probability of getting an odd number?

The number of favorable outcomes are: 1, 3, and 5. Total outcomes = 5 Probability = Number of favorable outcomes / Total outcomes. = 3/5 = 0.6 or 60%.

Question 9: What is the probability of not drawing a face card (Jack, Queen, King) from a standard deck of 52 cards?

Total face cards in the deck = 12 (4 Jacks, 4 Queens, 4 Kings). Total non-face cards = 52 - 12 = 40. Probability of not drawing a face card = Number of non-face cards / Total cards. = 40 / 52 = 10 / 13 ≈ 0.7692 or 76.92%.

Question 10: A jar contains 10 balls: 3 red and 7 black. What is the probability of drawing a red ball on a single draw?

Probability of drawing a red ball and replacing it = 3/10. Total probability = (3/10) =0.3 or 30%.

Question 11: In a class of 60 students, 30 are boys. If one student is randomly selected, what is the probability of selecting a girl?

Total girls = 60 - 30 = 30. Probability of chosen student being a girl = 30/60. = 0.5 or 50%

Question 12: A fair six-sided die is rolled. What is the probability of rolling a number greater than 4?

Total number of favorable outcome 5,6 Probability = 2/6 ​= 1/3​ =0.333 or 33.33%.

Practice Problems on Probability

• A jar contains 6 balls: 2 are red, 1 is yellow, and 3 are blue. What is the probability of picking a blue ball?
• A fair six-sided die is rolled. What is the probability of rolling a number less than 3?
• A jar contains 4 red, 5 green, and 6 blue marbles. What is the probability of randomly drawing a green marble?
• From a deck of 52 cards, what is the probability of drawing a Queen?
• A spinner with numbers 1 to 10 is spun once. What is the probability of spinning a number greater than 7?
• A bag contains 3 red marbles, 4 green marbles, and 3 blue marbles. What is the probability of drawing a green marble?
• In a class of 25 students, 10 are boys. What is the probability of randomly selecting a boy?
• A coin is flipped once. What is the probability of getting tails?
• A deck of 52 cards is shuffled. What is the probability of not drawing an Ace?
• A fair six-sided die is rolled. What is the probability of rolling an odd number?
• A jar contains 9 balls: 3 are red, 2 are green, and 4 are yellow. What is the probability of drawing a yellow ball?
• In a group of 30 students, 18 like cricket and 12 like football. If one student is randomly selected, what is the probability that they like football?
• Probability= 0.5 or 50%.
• Probability = 0.333 or 33.33%.
• Probability = 1/3 = 0.333 or 33.33%.
• Probability = 1/13 ≈ 0.0769 or 7.69%.
• Probability = 3/10 = 0.3 or 30%.
• Probability = 4/10 = 0.4 or 40%.
• Probability = 10/25 = 2.5 = 0.4 or 40%.
• Probability = 1/2 =0.5 or 50%.
• Probability = 48/52 = 12/13 ≈ 0.923 or 92.3%.
• Probability = 3/6 = 1/2 = 0.5 or 50%.
• Probability = 49 ≈ 0.444 or 44.44%.
• Probability = 12/30 = 25 = 0.4 or 40%.

Similar Reads

• Practice Problems on Probability (Easy) Probability is an important chapter for the students of Class 9, 10, 11, and 12. The Probability Questions, with their answers included in this article, will help you understand the basic concepts and formulas through a number of solved and unsolved questions. These questions cover concepts like Sam 6 min read
• Practice Problems on Probability (Hard) Probability is an important chapter for the students of Class 9, 10, 11, and 12. The Probability Questions, with their answers included in this article, will help you understand the basic concepts and formulas through a number of solved and unsolved questions. These questions cover concepts like Sam 9 min read
• Practice Problems on Probability (Medium) Probability is an important chapter for the students of Class 9, 10, 11, and 12. The Probability Questions, with their answers included in this article, will help you understand the basic concepts and formula through number of solved and unsolved questions. These questions cover concepts like Sample 8 min read
• Practice Problems on Probability | Class 9 Maths Probability, in simple words, is the prediction of the happening of an event before it has already happened. We predict many things in our day-to-day lives, like: Predict the weather before going for a picnic.Predict who is going to win the election.Predict the outcome of the toss.In all these situa 11 min read
• Conditional Probability Practice Question Conditional probability is a measure of the probability of an event occurring given that another event has already occurred. In simple words, conditional probability is like figuring out the chances of something happening given that something else has already happened. The probability of A given tha 7 min read
• Random Experiment - Probability In a cricket match, before the game begins. Two captains go for a toss. Tossing is an activity of flipping a coin and checking the result as either “Head” or “Tail”. Similarly, tossing a die gives us a number from 1 to 6. All these activities are examples of experiments. An activity that gives us a 12 min read
• Addition Rule for Probability Probability is an experimental approach to the game of chances we come across every day in our lives. It is a way to describe these “chances” mathematically and then analyze them. It allows us to measure the chances of something occurring. Probability of Event P(E) = [Number of Favorable Outcomes] / 10 min read
• Types of Events in Probability Whenever an experiment is performed whose outcomes cannot be predicted with certainty, it is called a random experiment. In such cases, we can only measure which of the events is more likely or less likely to happen. This likelihood of events is measured in terms of probability and events refer to t 13 min read
• Axiomatic Approach to Probability Hearing the word "probability" brings up ideas related to uncertainty or randomness. Although the concept of probability can be hard to describe formally, it helps us analyze how likely it is that a certain event will happen. This analysis helps us understand and describe many phenomena we see in re 10 min read
• Chance and Probability Chance is defined as the natural occurrence of any event without any interference, we can also say that the possibility of any event is the chance of the event, and mathematically we define the chance as the probability of an event. Probability refers to the likelihood of the occurrence of an event. 9 min read
• Properties of Probability ProbabilityProbability is the branch of mathematics that is concerned with the chances of occurrence of events and possibilities. Further, it gives a method of measuring the probability of uncertainty and predicting events in the future by using the available information. Probability is a measure of 14 min read
• Dice Rolling Probability Calculator A classic example of probability and statistics is a dice thrown. It’s often used to demonstrate some basic principles of probability. Therefore, students need to know about dice probabilities because they form the bedrock for more complicated statistical concepts commonly used in games and real-lif 6 min read
• Probability Distribution - Function, Formula, Table A probability distribution describes how the probabilities of different outcomes are assigned to the possible values of a random variable. It provides a way of modeling the likelihood of each outcome in a random experiment. While a frequency distribution shows how often outcomes occur in a sample or 15+ min read
• Aptitude | Probability | Question 2 A and B appeared for an exam. Let A is selected when even x happens and B is selected if the event y happens. The probability of event x is 1/7 and that of y is 2/9. Find the probability that both A and B got selected. (A) 7/15 (B) 3/14 (C) 2/63 (D) 6/63 Answer: (C) Explanation: Since selection of A 1 min read
• Probability of At Least One Probability of at least one normally describes the chance that an event will take place at least once within a sequence of chances or trials. This concept is widely applicable in various fields, from predicting the chances of at least one rainy day in a week to assessing the risk of at least one mac 5 min read
• Random Variables Practice Problems Random variables are fundamental concepts in probability and statistics, playing a crucial role in data analysis and decision-making processes. Understanding random variables is essential for students as it lays the groundwork for advanced topics such as statistical inference, regression analysis an 8 min read
• Probability Rules Probability is a crucial concept in mathematics and statistics that enables us to quantify uncertainty and make informed decisions in various fields. Whether it's predicting the outcome of an experiment or assessing risk in finance, probability rules provide a systematic way to analyze and understan 8 min read
• Poisson Distribution Practice Problems Poisson distribution is a probability distribution that models the number of events occurring within a fixed interval of time or space, where these events happen with a known constant mean rate and independently of the time since the last event. It is named after the French mathematician Siméon Deni 5 min read
• Empirical Probability Empirical Probability: Probability describes the chance that an uncertain event will occur. Empirical probability is based on how likely an event has occurred in the past. It is also called experimental probability. It is based on the relative frequency approach. We can get our results from experien 7 min read
• School Learning
• Math-Queries

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Probability Questions with Solutions

Tutorial on finding the probability of an event. In what follows, S is the sample space of the experiment in question and E is the event of interest. n(S) is the number of elements in the sample space S and n(E) is the number of elements in the event E.

Questions and their Solutions

Answers to the above exercises, more references and links.

• Probability Questions Answers

Worked-out probability questions answers are given here step-by-step to get the clear explanation to the student.  

1. Out of 300 students in a school, 95 play cricket only, 120 play football only, 80 play volleyball only and 5 play no games. If one student is chosen at random, find the probability that

(i) he plays volleyball

(ii) he plays either cricket or volleyball

(iii) he plays neither football nor volleyball.

Total number of trials = 300 (Since there are 300 students all together).

Number of times a cricket player is chosen = 95 (Since 95 students play cricket).

Number of times a football player is chosen = 120.

Number of times a volleyball player is chosen = 80.

Number of times a student is chosen who plays no games = 5.

(i) Therefore, the probability of getting a player who plays volleyball

                                     = \(\frac{\textrm{Number of Times a Volleyball Player can be Chosen}}{\textrm{Total Number of Trials}}\)

                                     = \(\frac{80}{300}\)

                                                   = \(\frac{4}{15}\).

(ii) The probability of getting a player who plays either cricket or volleyball

                             = \(\frac{\textrm{Number of Times a Cricket or a Volleyball Player can be Chosen}}{\textrm{Total Number of Trials}}\)

                             = \(\frac{95 + 80}{300}\)

                             = \(\frac{175}{300}\)

                             = \(\frac{7}{12}\).

(iii) The probability of getting a player who plays neither football nor volleyball = \(\frac{\textrm{Number of Times a Student can be Chosen who do not Play Football or Volleyball}}{\textrm{Total Number of Trials}}\)

             = \(\frac{300 – 120 - 80}{300}\)

             = \(\frac{100}{300}\)

             = \(\frac{1}{3}\).

2.  The blood group of 60 students of a class recorded as below.

A student of the class is selected at random.

(i) What is the probability that the selected student has blood group O?

(ii) What is the probability that the selected student does not have blood group O?

(i) Total number of trials = 60. [Since, there are 60 different students).

Number of students having blood group O = 18.

So, the probability of the student’s blood group being O

                        = \(\frac{\textrm{Frequency of Favourable Trials}}{\textrm{Total Number of Trials}}\)

                        = \(\frac{\textrm{Number of Students having Blood Group O}}{\textrm{Total Number of Trials}}\)

                       = \(\frac{18}{60}\)

                       = \(\frac{3}{10}\).

(ii) Total number of trials = 60. [Since, there are 60 different students).

Number of students not having blood group O = Total Number of Students - Number of Students having Blood Group O = 60 – 18 = 42.

So, the probability of the student’s blood group being different from O

                        = \(\frac{\textrm{Number of Students not having Blood Group O}}{\textrm{Total Number of Trials}}\)

                        = \(\frac{42}{60}\)

                       = \(\frac{7}{10}\).

Note: Probability of the student’s blood group not being O = \(\frac{3}{10}\) + \(\frac{7}{10}\) = 1.

3. In a test of 100 marks, the marks scored by the students of a class are given below.

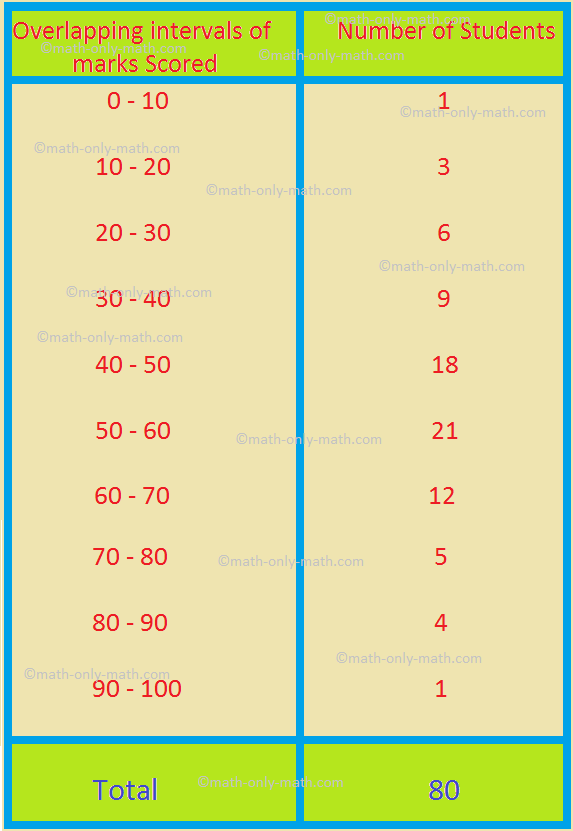
A student of the class is selected at random. Find the probability that the student has scored

(i) less than 30

(ii) at least 60

(iii) not less than 80.

(i) Total number of trials = 80 [Since there are 80 students all together].

Number of students scoring less than 30 = Cumulative frequency of the interval 20 – 30 = 1 + 3 + 6 = 10.

So, the probability of the student scoring less than 30

                            = \(\frac{\textrm{Frequency of Favourable Trials}}{\textrm{Total Number of Trials}}\)

                            = \(\frac{\textrm{Number of Students Scoring Less than 30}}{\textrm{Total Number of Students}}\)

                             = \(\frac{10}{80}\)

                             = \(\frac{1}{8}\).

(ii) Total number of trials = 80.

Number of students scoring at least 60 = Number of students scoring more than or equal to 60

= 12 + 5 + 4 + 1 (= Sum of frequencies of the intervals 60 – 70, 70 – 80, 80 – 90, 90 – 100)

So, the required probability = \(\frac{\textrm{Frequency of Favourable Trials}}{\textrm{Total Number of Trials}}\)

                                         = \(\frac{\textrm{Number of Students Scoring at least 60}}{\textrm{Total Number of Students}}\)

                                         = \(\frac{22}{80}\)

                                         = \(\frac{11}{40}\).

(iii) Total number of trials = 80.

Number of students scoring at not less than 80 = Number of students scoring to least 80

= 4 + 1 (= Sum of frequencies of the intervals 80 – 90 and 90 – 100)

Therefore, the required probability = \(\frac{\textrm{Number of Students Scoring not less than 80}}{\textrm{Total Number of Students}}\)

                                                   = \(\frac{5}{80}\)

                                                   = \(\frac{1}{16}\).

4. A bag contains 8 red balls and some white balls. If the probability of drawing a white ball is half of the probability of drawing a red ball then find the number of white balls in the bag.

Let the number of white balls be n. 

The number of red balls = 8.

Therefore, the possible number of outcomes = n + 8.

Now, the probability of drawing a white ball = \(\frac{n}{n + 8}\).

The probability of drawing a red ball = \(\frac{8}{n + 8}\).

Now, from question,

\(\frac{n}{n + 8}\) = \(\frac{1}{2}\) ∙ \(\frac{n}{n + 8}\)

So, number of white balls in the bag is 4.

5. A box contains 90 discs numbered 1 to 90. One disc is drawn at random from the box. What is the probability that is bears

(i) a two-digit number

(ii) a perfect square

(iii) a multiply of 5

(iv) a number divisible by 3 and 5.

(i) Total number of possible outcomes = 90 (Since the disks are numbered from 1 to 90).

Number of favourable outcomes of the event E

                  = Number of two-digit numbers from 1 to 90

                  = 90 - 9 = 81 (Since all are two-digit numbers except 1 to 9)

Therefore, P(E) = \(\frac{\textrm{Number of Favourable Outcomes of the Event E}}{\textrm{Total Number of Possible Outcomes}}\)

                       = \(\frac{81}{90}\)

                       = \(\frac{9}{10}\).

(ii) Total number of possible outcomes = 90.

Number of favourable outcomes of the event F

                         = Number of perfect squares from 1 to 90

                         = 9   [Since 1, 4, 9, 16, 25, 36, 49, 64 and 81 are perfect squares).

Therefore, by definition, P(F) = \(\frac{9}{90}\)

                                           = \(\frac{1}{10}\).

(iii) Total number of possible outcomes = 90.

Number of favourable outcomes of the event G

             = Number of multiples of 5 among numbers from 1 to 90

             = 18   [Since 5 × 1, 5 × 2, 5 × 3, ....,  5 × 18 are multiple of 5).

Therefore, by definition, P(G) = \(\frac{18}{90}\)

                                           = \(\frac{1}{5}\).

(iv) Total number of possible outcomes = 90.

Number of favourable outcomes of the event H

       = Number of numbers divisible by 3 and 5 from 1 to 90

       = Number of numbers divisible by 15 from 1 to 90

       = 6  [Since 15 × 1, 15 × 2, 15 × 3, ....,  15 × 6 are divisible by 15).

Therefore, by definition, P(H) = \(\frac{6}{90}\)

                                           = \(\frac{1}{15}\).

●   Probability

• Probability
• Definition of Probability
• Random Experiments
• Experimental Probability
• Events in Probability
• Empirical Probability
• Coin Toss Probability
• Probability of Tossing Two Coins
• Probability of Tossing Three Coins
• Complimentary Events
• Mutually Exclusive Events
• Mutually Non-Exclusive Events
• Conditional Probability
• Theoretical Probability
• Odds and Probability
• Playing Cards Probability
• Probability and Playing Cards
• Probability Rolling a Die
• Probability for Rolling Two Dice
• Probability for Rolling Three Dice
• Solved Probability Problems
• 10th Grade Math

From  Probability Questions Answers  to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments

Share this page: What’s this?

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

3rd Grade Number Worksheet |Practice the Questions on Numbers with Ans

Dec 23, 24 03:10 AM

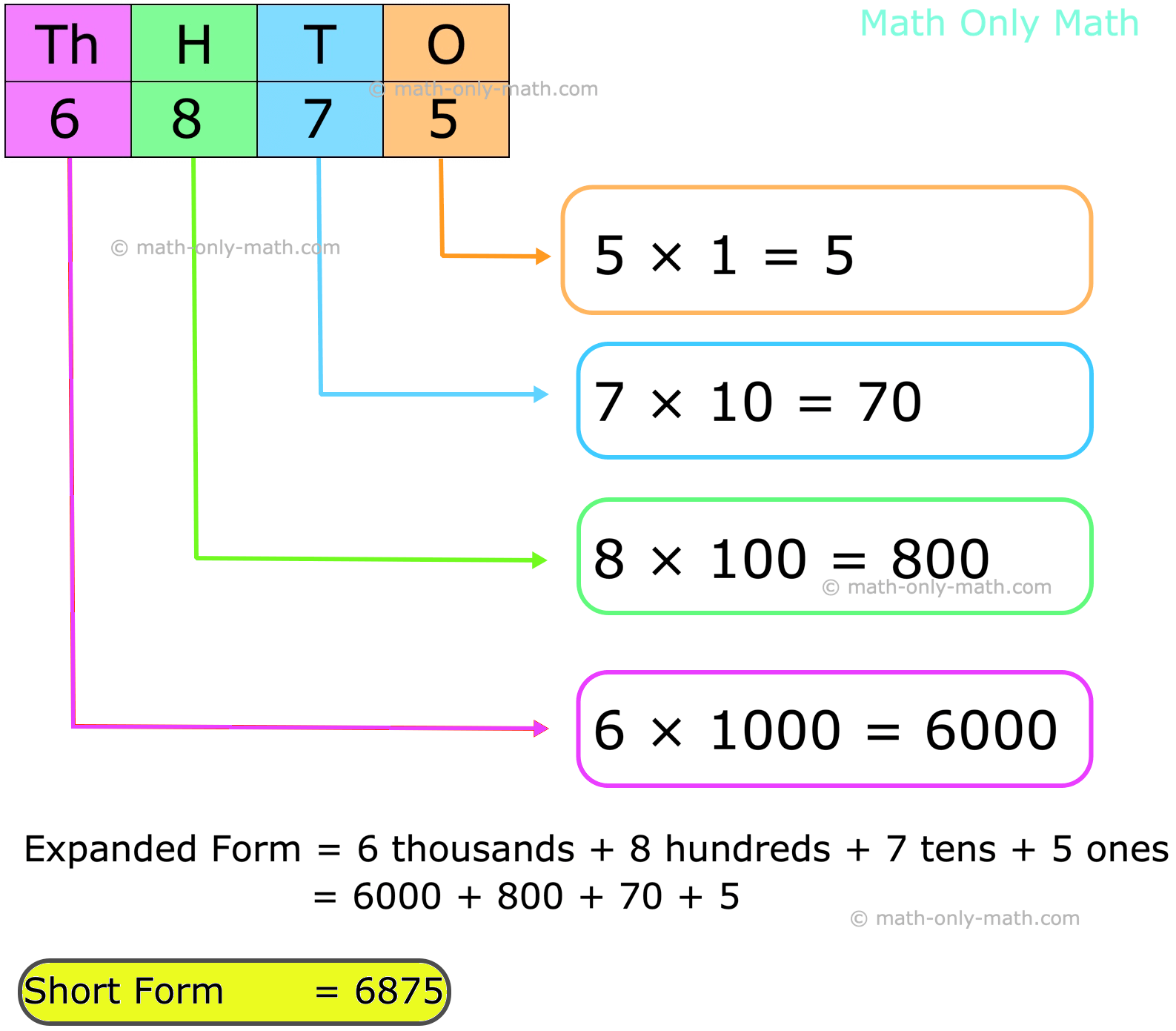
Expanded Form and Short Form of a Number | Numbers in Expanded Form

Dec 23, 24 02:39 AM

Rounding off Numbers | Nearest Multiple of 10 | Nearest Whole Number

Dec 22, 24 04:09 PM

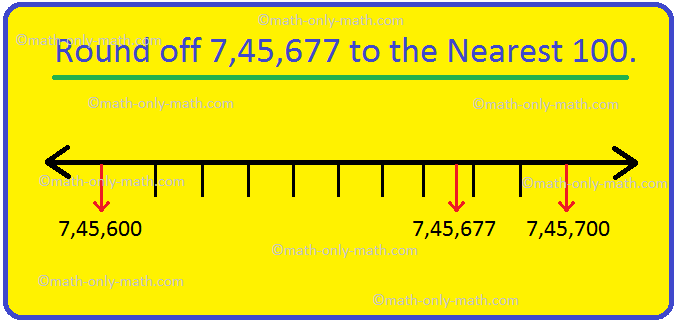
Round off to Nearest 100 | Rounding Numbers To Nearest Hundred | Rules

Dec 22, 24 03:40 PM

Round off to Nearest 1000 |Rounding Numbers to Nearest Thousand| Rules

Dec 22, 24 03:39 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

• High School
• You don't have any recent items yet.
• You don't have any courses yet.
• You don't have any books yet.
• You don't have any Studylists yet.
• Information

Probability HM - All correct answers for this assignment.

Statistics for the social sciences (psyc 354), liberty university.

Recommended for you

Students also viewed.

• Probability Template
• SPSS Homework One Sample t Test and Cumulative Questions Template
• Annotated-SPSS%20Homework%20Central%20Tendency%20Assignment%20
• Probability Template - good
• Hypothesis Testing Template

Related documents

• Wk 8 Final Psych 354
• SPSS Homework Testing Data for Normality
• SPSS Homework Variability DONE
• SPSS Homework Frequency Tables, Histograms, and Bar Charts Assignment Instructions
• SPSS Homework Frequency Tables, Histograms, and Bar Charts Template
• PSYC354 Quiz 2 - Quiz 2

Preview text

Probability assignment_hm, questions 1-, fill in the highlighted blanks to answer/complete the statements. use the textbook as your, resource for these definitions. (3 pts each), 1) the particular score associated with a percentile rank is known as a percentile rank ., the area in a distribution can be divided into four equal parts called quartiles ., in independent random sampling, sampling__ with replacement is the process of, returning each individual to the population before making the next selection., probabilities are expressed within a limited range. the lower limit of the range is o ,, which indicates an event that never occurs; and the higher limit of the range is 1 ,, which indicates an event that always occurs., the standard normal table lists proportions of the normal distribution for a full, range of possible z-score values., questions 6-, complete the following exercises: (2 pts each), 6) what is the probability of, hitting a target if, in the long, run, 4 out of every 24 attempts, actually hit the target (3 pts), answer (show work): 4/24 + 1/6 or 0., 7) on a tv game show, 25, people have won the grand, prize and a total of 350 people, have competed. estimate the, probability of winning the, grand prize. (3 pts), answer (show work): 25/350 = 0., 8) convert the following, decimals to percentages: (2 pts, a) answer: 65% b) answer: 83%, 9) convert the following, percentages to decimals: (2 pts, a) answer: 0 b) answer: 0 c, page 1 of 3, 10) using the z table in appendix b (table b-1), calculate the following percentages for a z, score of +0. describe how you used the table to find these values. (4 pts each for a and b), 10-a) % above this z, score (in the tail):, answer: 21%, work (describe your process here):, find the % of the values in the tail for z score o by looking it, up in the z table and subtracting its corresponding value from, 10-b) % below this z, score (in the body):, answer: 78%, find the value for o in a table. the value is 0, which is, the percentage below 0., 11) rewrite each of the following percentages as probabilities, or p-values, which are, expressed in decimal format: (2 pts each), 11-a) 64% answer: p = 0., 11-b) 19% answer: p = 0., 11-c) 4% answer: p = 0., 11-d) 5% answer: p =0., 12) a certain clinical measure of anxiety has a cut-off of z = +2, meaning that z-scores, higher than this indicate severe levels of anxiety that may require treatment. two of your, clients have the z-scores listed below. based on the given score and the information here,, would you recommend that the client be further evaluated for anxiety treatment explain, your reasoning. evaluate each client independently. (3 pts each), 12a) z = -1 answer: no, the client does not have severe anxiety and wont need, explanation: a score of -1 is lower than +2, which means the client’s anxiety is not, severe enough to be prescribed treatment according to this measure., 12b) z = +2 answer: yes, the client should be checked for anxiety and seek treatment, explanation: the clien’ts anxiety level is very high and they may need treatment for, page 2 of 3.

• Multiple Choice

Course : Statistics for the Social Sciences (PSYC 354)

University : liberty university.

• More from: Statistics for the Social Sciences PSYC 354 Liberty University 86   Documents Go to course