examples of systematic errors in experiments

• Science, Tech, Math ›
• Chemistry ›
• Scientific Method ›

Random Error vs. Systematic Error

Two Types of Experimental Error

• Scientific Method
• Chemical Laws
• Periodic Table
• Projects & Experiments
• Biochemistry
• Physical Chemistry
• Medical Chemistry
• Chemistry In Everyday Life
• Famous Chemists
• Activities for Kids
• Abbreviations & Acronyms
• Weather & Climate
• Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
• B.A., Physics and Mathematics, Hastings College

No matter how careful you are, there is always some error in a measurement. Error is not a "mistake"—it's part of the measuring process. In science, measurement error is called experimental error or observational error.

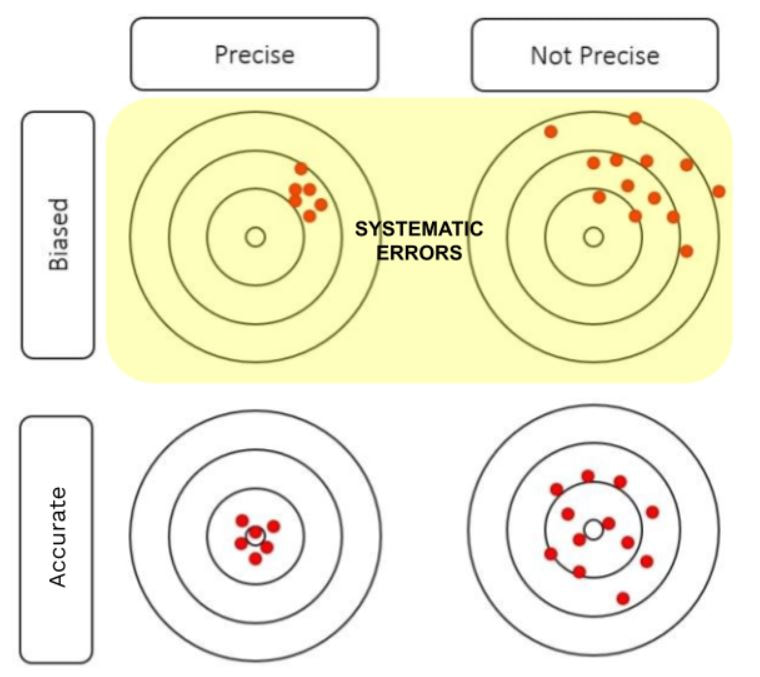
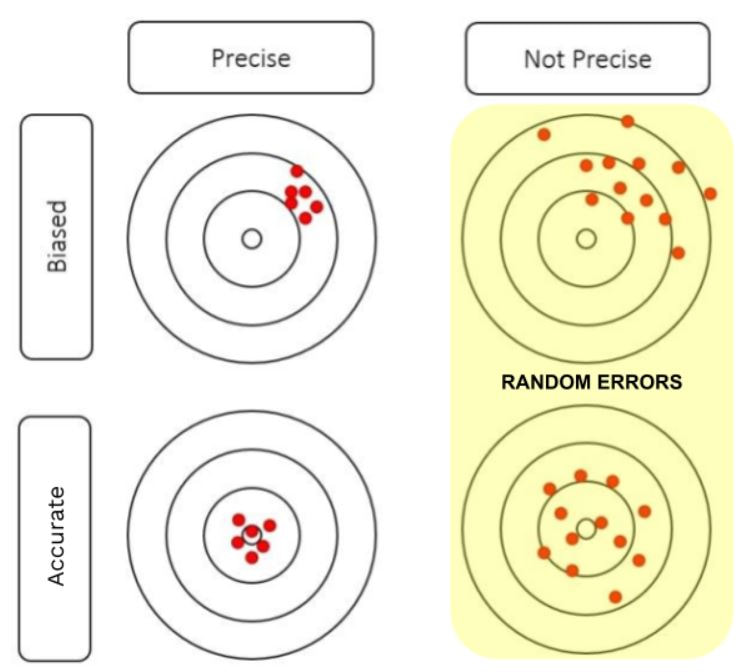
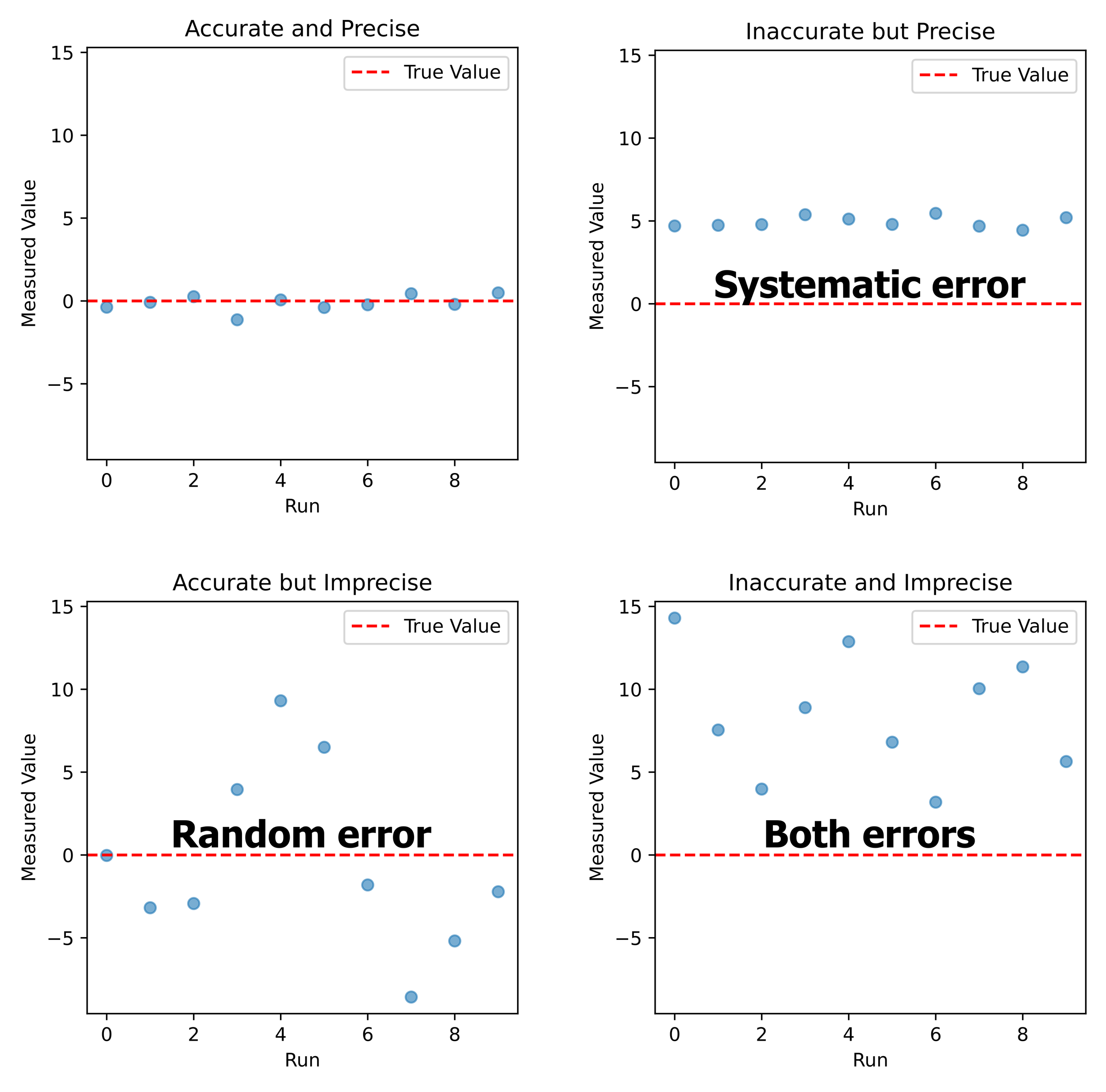
There are two broad classes of observational errors: random error and systematic error. Random error varies unpredictably from one measurement to another, while systematic error has the same value or proportion for every measurement. Random errors are unavoidable but cluster around the true value. Systematic error can often be avoided by calibrating equipment, but if left uncorrected, it can lead to measurements far from the true value.

Key Takeaways

• The two main types of measurement error are random error and systematic error.
• Random error causes one measurement to differ slightly from the next. It comes from unpredictable changes during an experiment.
• Systematic error always affects measurements by the same amount or proportion, provided that a reading is taken the same way each time. It is predictable.
• Random errors cannot be eliminated from an experiment, but most systematic errors may be reduced.

Systematic Error Examples and Causes

Systematic error is predictable and either constant or proportional to the measurement. Systematic errors primarily influence a measurement's accuracy .

What Causes Systematic Error?

Typical causes of systematic error include observational error, imperfect instrument calibration, and environmental interference. For example:

• Forgetting to tare or zero a balance produces mass measurements that are always "off" by the same amount. An error caused by not setting an instrument to zero prior to its use is called an offset error.
• Not reading the meniscus at eye level for a volume measurement will always result in an inaccurate reading. The value will be consistently low or high, depending on whether the reading is taken from above or below the mark.
• Measuring length with a metal ruler will give a different result at a cold temperature than at a hot temperature, due to thermal expansion of the material.
• An improperly calibrated thermometer may give accurate readings within a certain temperature range, but become inaccurate at higher or lower temperatures.
• Measured distance is different using a new cloth measuring tape versus an older, stretched one. Proportional errors of this type are called scale factor errors.
• Drift occurs when successive readings become consistently lower or higher over time. Electronic equipment tends to be susceptible to drift. Many other instruments are affected by (usually positive) drift, as the device warms up.

How Can You Avoid Systematic Error?

Once its cause is identified, systematic error may be reduced to an extent. Systematic error can be minimized by routinely calibrating equipment, using controls in experiments, warming up instruments before taking readings, and comparing values against standards .

While random errors can be minimized by increasing sample size and averaging data, it's harder to compensate for systematic error. The best way to avoid systematic error is to be familiar with the limitations of instruments and experienced with their correct use.

Random Error Examples and Causes

If you take multiple measurements , the values cluster around the true value. Thus, random error primarily affects precision . Typically, random error affects the last significant digit of a measurement.

What Causes Random Error?

The main reasons for random error are limitations of instruments, environmental factors, and slight variations in procedure. For example:

• When weighing yourself on a scale, you position yourself slightly differently each time.
• When taking a volume reading in a flask, you may read the value from a different angle each time.
• Measuring the mass of a sample on an analytical balance may produce different values as air currents affect the balance or as water enters and leaves the specimen.
• Measuring your height is affected by minor posture changes.
• Measuring wind velocity depends on the height and time at which a measurement is taken. Multiple readings must be taken and averaged because gusts and changes in direction affect the value.
• Readings must be estimated when they fall between marks on a scale or when the thickness of a measurement marking is taken into account.

How Can You Avoid (or Minimize) Random Error?

Because random error always occurs and cannot be predicted , it's important to take multiple data points and average them to get a sense of the amount of variation and estimate the true value. Statistical techniques such as standard deviation can further shed light on the extent of variability within a dataset.

Cochran, W. G. (1968). "Errors of Measurement in Statistics". Technometrics. Taylor & Francis, Ltd. on behalf of American Statistical Association and American Society for Quality. 10: 637–666. doi:10.2307/1267450

Bland, J. Martin, and Douglas G. Altman (1996). "Statistics Notes: Measurement Error." BMJ 313.7059: 744.

Taylor, J. R. (1999). An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books. p. 94. ISBN 0-935702-75-X.

• Null Hypothesis Examples
• The Role of a Controlled Variable in an Experiment
• Scientific Method Vocabulary Terms
• Six Steps of the Scientific Method
• What Are Examples of a Hypothesis?
• What Is an Experimental Constant?
• Understanding Simple vs Controlled Experiments
• DRY MIX Experiment Variables Acronym
• Scientific Hypothesis Examples
• What Is a Testable Hypothesis?
• What Is the Difference Between a Control Variable and Control Group?
• What Are the Elements of a Good Hypothesis?
• What Is a Hypothesis? (Science)
• Scientific Method Flow Chart
• What Is a Controlled Experiment?
• Scientific Variable

• Science Notes Posts
• Contact Science Notes
• Todd Helmenstine Biography
• Anne Helmenstine Biography
• Free Printable Periodic Tables (PDF and PNG)
• Periodic Table Wallpapers
• Interactive Periodic Table
• Periodic Table Posters
• Science Experiments for Kids
• How to Grow Crystals
• Chemistry Projects
• Fire and Flames Projects
• Holiday Science
• Chemistry Problems With Answers
• Physics Problems
• Unit Conversion Example Problems
• Chemistry Worksheets
• Biology Worksheets
• Periodic Table Worksheets
• Physical Science Worksheets
• Science Lab Worksheets
• My Amazon Books

Sources of Error in Science Experiments

Science labs usually ask you to compare your results against theoretical or known values. This helps you evaluate your results and compare them against other people’s values. The difference between your results and the expected or theoretical results is called error. The amount of error that is acceptable depends on the experiment, but a margin of error of 10% is generally considered acceptable. If there is a large margin of error, you’ll be asked to go over your procedure and identify any mistakes you may have made or places where error might have been introduced. So, you need to know the different types and sources of error and how to calculate them.

How to Calculate Absolute Error

One method of measuring error is by calculating absolute error , which is also called absolute uncertainty. This measure of accuracy is reported using the units of measurement. Absolute error is simply the difference between the measured value and either the true value or the average value of the data.

absolute error = measured value – true value

For example, if you measure gravity to be 9.6 m/s 2 and the true value is 9.8 m/s 2 , then the absolute error of the measurement is 0.2 m/s 2 . You could report the error with a sign, so the absolute error in this example could be -0.2 m/s 2 .

If you measure the length of a sample three times and get 1.1 cm, 1.5 cm, and 1.3 cm, then the absolute error is +/- 0.2 cm or you would say the length of the sample is 1.3 cm (the average) +/- 0.2 cm.

Some people consider absolute error to be a measure of how accurate your measuring instrument is. If you are using a ruler that reports length to the nearest millimeter, you might say the absolute error of any measurement taken with that ruler is to the nearest 1 mm or (if you feel confident you can see between one mark and the next) to the nearest 0.5 mm.

How to Calculate Relative Error

Relative error is based on the absolute error value. It compares how large the error is to the magnitude of the measurement. So, an error of 0.1 kg might be insignificant when weighing a person, but pretty terrible when weighing a apple. Relative error is a fraction, decimal value, or percent.

Relative Error = Absolute Error / Total Value

For example, if your speedometer says you are going 55 mph, when you’re really going 58 mph, the absolute error is 3 mph / 58 mph or 0.05, which you could multiple by 100% to give 5%. Relative error may be reported with a sign. In this case, the speedometer is off by -5% because the recorded value is lower than the true value.

Because the absolute error definition is ambiguous, most lab reports ask for percent error or percent difference.

How to Calculate Percent Error

The most common error calculation is percent error , which is used when comparing your results against a known, theoretical, or accepted value. As you probably guess from the name, percent error is expressed as a percentage. It is the absolute (no negative sign) difference between your value and the accepted value, divided by the accepted value, multiplied by 100% to give the percent:

% error = [accepted – experimental ] / accepted x 100%

How to Calculate Percent Difference

Another common error calculation is called percent difference . It is used when you are comparing one experimental result to another. In this case, no result is necessarily better than another, so the percent difference is the absolute value (no negative sign) of the difference between the values, divided by the average of the two numbers, multiplied by 100% to give a percentage:

% difference = [experimental value – other value] / average x 100%

Sources and Types of Error

Every experimental measurement, no matter how carefully you take it, contains some amount of uncertainty or error. You are measuring against a standard, using an instrument that can never perfectly duplicate the standard, plus you’re human, so you might introduce errors based on your technique. The three main categories of errors are systematic errors, random errors , and personal errors. Here’s what these types of errors are and common examples.

Systematic Errors

Systematic error affects all the measurements you take. All of these errors will be in the same direction (greater than or less than the true value) and you can’t compensate for them by taking additional data. Examples of Systematic Errors

• If you forget to calibrate a balance or you’re off a bit in the calibration, all mass measurements will be high/low by the same amount. Some instruments require periodic calibration throughout the course of an experiment , so it’s good to make a note in your lab notebook to see whether the calibrations appears to have affected the data.
• Another example is measuring volume by reading a meniscus (parallax). You likely read a meniscus exactly the same way each time, but it’s never perfectly correct. Another person taking the reading may take the same reading, but view the meniscus from a different angle, thus getting a different result. Parallax can occur in other types of optical measurements, such as those taken with a microscope or telescope.
• Instrument drift is a common source of error when using electronic instruments. As the instruments warm up, the measurements may change. Other common systematic errors include hysteresis or lag time, either relating to instrument response to a change in conditions or relating to fluctuations in an instrument that hasn’t reached equilibrium. Note some of these systematic errors are progressive, so data becomes better (or worse) over time, so it’s hard to compare data points taken at the beginning of an experiment with those taken at the end. This is why it’s a good idea to record data sequentially, so you can spot gradual trends if they occur. This is also why it’s good to take data starting with different specimens each time (if applicable), rather than always following the same sequence.
• Not accounting for a variable that turns out to be important is usually a systematic error, although it could be a random error or a confounding variable. If you find an influencing factor, it’s worth noting in a report and may lead to further experimentation after isolating and controlling this variable.

Random Errors

Random errors are due to fluctuations in the experimental or measurement conditions. Usually these errors are small. Taking more data tends to reduce the effect of random errors. Examples of Random Errors

• If your experiment requires stable conditions, but a large group of people stomp through the room during one data set, random error will be introduced. Drafts, temperature changes, light/dark differences, and electrical or magnetic noise are all examples of environmental factors that can introduce random errors.
• Physical errors may also occur, since a sample is never completely homogeneous. For this reason, it’s best to test using different locations of a sample or take multiple measurements to reduce the amount of error.
• Instrument resolution is also considered a type of random error because the measurement is equally likely higher or lower than the true value. An example of a resolution error is taking volume measurements with a beaker as opposed to a graduated cylinder. The beaker will have a greater amount of error than the cylinder.
• Incomplete definition can be a systematic or random error, depending on the circumstances. What incomplete definition means is that it can be hard for two people to define the point at which the measurement is complete. For example, if you’re measuring length with an elastic string, you’ll need to decide with your peers when the string is tight enough without stretching it. During a titration, if you’re looking for a color change, it can be hard to tell when it actually occurs.

Personal Errors

When writing a lab report, you shouldn’t cite “human error” as a source of error. Rather, you should attempt to identify a specific mistake or problem. One common personal error is going into an experiment with a bias about whether a hypothesis will be supported or rejects. Another common personal error is lack of experience with a piece of equipment, where your measurements may become more accurate and reliable after you know what you’re doing. Another type of personal error is a simple mistake, where you might have used an incorrect quantity of a chemical, timed an experiment inconsistently, or skipped a step in a protocol.

Related Posts

Learn The Types

Learn About Different Types of Things and Unleash Your Curiosity

Understanding Experimental Errors: Types, Causes, and Solutions

Types of experimental errors.

In scientific experiments, errors can occur that affect the accuracy and reliability of the results. These errors are often classified into three main categories: systematic errors, random errors, and human errors. Here are some common types of experimental errors:

1. Systematic Errors

Systematic errors are consistent and predictable errors that occur throughout an experiment. They can arise from flaws in equipment, calibration issues, or flawed experimental design. Some examples of systematic errors include:

– Instrumental Errors: These errors occur due to inaccuracies or limitations of the measuring instruments used in the experiment. For example, a thermometer may consistently read temperatures slightly higher or lower than the actual value.

– Environmental Errors: Changes in environmental conditions, such as temperature or humidity, can introduce systematic errors. For instance, if an experiment requires precise temperature control, fluctuations in the room temperature can impact the results.

– Procedural Errors: Errors in following the experimental procedure can lead to systematic errors. This can include improper mixing of reagents, incorrect timing, or using the wrong formula or equation.

2. Random Errors

Random errors are unpredictable variations that occur during an experiment. They can arise from factors such as inherent limitations of measurement tools, natural fluctuations in data, or human variability. Random errors can occur independently in each measurement and can cause data points to scatter around the true value. Some examples of random errors include:

– Instrument Noise: Instruments may introduce random noise into the measurements, resulting in small variations in the recorded data.

– Biological Variability: In experiments involving living organisms, natural biological variability can contribute to random errors. For example, in studies involving human subjects, individual differences in response to a treatment can introduce variability.

– Reading Errors: When taking measurements, human observers can introduce random errors due to imprecise readings or misinterpretation of data.

3. Human Errors

Human errors are mistakes or inaccuracies that occur due to human factors, such as lack of attention, improper technique, or inadequate training. These errors can significantly impact the experimental results. Some examples of human errors include:

– Data Entry Errors: Mistakes made when recording data or entering data into a computer can introduce errors. These errors can occur due to typographical mistakes, transposition errors, or misinterpretation of results.

– Calculation Errors: Errors in mathematical calculations can occur during data analysis or when performing calculations required for the experiment. These errors can result from mathematical mistakes, incorrect formulas, or rounding errors.

– Experimental Bias: Personal biases or preconceived notions held by the experimenter can introduce bias into the experiment, leading to inaccurate results.

It is crucial for scientists to be aware of these types of errors and take measures to minimize their impact on experimental outcomes. This includes careful experimental design, proper calibration of instruments, multiple repetitions of measurements, and thorough documentation of procedures and observations.

You Might Also Like:

Patio perfection: choosing the best types of pavers for your outdoor space, a guide to types of pupusas: delicious treats from central america, exploring modern period music: from classical to jazz and beyond.

• A1.1: Water
• A1.2: Nucleic Acids
• A2.1: Origins of Cells
• A2.2: Cell Structure
• A2.3: Viruses
• A3.1: Diversity of Organisms
• A3.2: Classification and Cladistics
• A4.1: Evolution and Speciation
• A4.2: Conservation of Biodiversity
• B1.1: Carbohydrates and Lipids
• B1.2: Proteins
• B2.1 Membranes and Membrane Transport
• B2.2 Organelles and Compartmentalization
• B2.3 Cell Specialization
• B3.1 Gas Exchange
• B3.2 Transport
• B3.3 Muscle and Motility
• B4.1 Adaptation to Environment
• B4.2 Ecological Niches
• C1.1: Enzymes and Metabolism
• C1.2: Cell Respiration
• C1.3: Photosynthesis
• C2.1: Chemical Signaling
• C2.2: Neural Signaling
• C3.1: Integration of Body Systems
• C3.2: Defense Against Disease
• C4.1 Populations and Communities
• C4.2 Transfers of Energy and Matter
• D1.1: DNA Replication
• D1.2: Protein Synthesis
• D1.3: Mutation and Gene Editing
• D2.1: Cell and Nuclear Division
• D2.2: Gene Expression
• D2.3: Water Potential
• D3.1: Reproduction
• D3.2: Inheritance
• D3.3: Homeostasis
• D4.1: Natural Selection
• D4.2: Stability and Change
• D4.3: Climate Change
• 1.1: Introduction to Cells
• 1.2: Ultrastructure of Cells
• 1.3: Membrane Structure
• 1.4: Membrane Transport
• 1.5: The Origin of Cells
• 1.6: Cell Division
• 2.1: Molecules to Metabolism
• 2.3: Carbohydrates and Lipids
• 2.4: Proteins
• 2.5: Enzymes
• 2.6: DNA and RNA
• 2.7: DNA Replication, Transcription and Translation
• 2.8: Cell Respiration
• 2.9: Photosynthesis
• 3.2: Chromosomes
• 3.3: Meiosis
• 3.4: Inheritance
• 3.5: Genetic Modification and Biotechnology
• 4.1: Species, Communities and Ecosystems
• 4.2: Energy Flow
• 4.3: Carbon Cycling
• 4.4: Climate Change
• 5.1: Evidence for Evolution
• 5.2: Natural Selection
• 5.3: Classification and Biodiversity
• 5.4: Cladistics
• 6.1: Digestion and Absorption
• 6.2: The Blood System
• 6.3: Defense Against Infectious Disease
• 6.4: Gas Exchange
• 6.5: Neurons and Synapses
• 6.6: Hormones, Homeostasis and Reproduction
• 7.1: DNA Structure and Replication
• 7.2: Transcription and Gene Expression
• 7.3: Translation
• 8.1: Metabolism
• 8.2: Cell Respiration
• 8.3: Photosynthesis
• 9.1: Transport in the Xylem of Plants
• 9.2: Transport in the Phloem of Plants
• 9.3: Growth in Plants
• 9.4: Reproduction in Plants
• 10.1: Meiosis
• 10.2: Inheritance
• 10.3: Gene Pools and Speciation
• 11.1: Antibody Production and Vaccination
• 11.2: Movement
• 11.3: Kidney and Osmoregulation
• 11.4: Sexual Reproduction
• D.1: Human Nutrition
• D.2: Digestion
• D.3: Functions of the Liver
• D.4: The Heart
• D.5: Hormones and Metabolism
• D.6: Transport of Respiratory Gases
• Revision Tools
• Learner Profile
• Collaborative Sciences Project
• External Assessment
• Research Design
• Extended Essay
• Exam Revision
• Addressing Safety
• Lab Drawings
• Measurement Uncertainty
• Graphing with Excel
• Glossary of Statistic Terms and Equations
• Skew and the Normal Distribution
• Measures of Central Tendancy
• Measures of Spread
• Pearson Correlation
• Kruskal-Wallis
• X2 Test for Independence
• X2 Goodness of Fit
• Interpreting Error Bars
• Research Questions
• Hypotheses and Predictions
• Data Tables
• Error Analysis
• Biology Club
• Pumpkin Carving
• Scavenger Hunt
• Science News
• Wood Duck Project (legacy)
• Invasive Crayfish Project (legacy)
• Class Grading IB Bio I
• Class Grading IB Bio II
• Daily Quizzes (legacy)
• Lab Practicals (legacy)
• Class Photos
• Recommendations
• Favorite Quotes
• Bahamas (2009)
• Trinidad (2010)
• Trinidad (2011)
• Ecuador (2012)
• Trinidad (2013)
• Peru (2014)
• Bahamas (2015)
• Peru (2016)
• Costa Rica (2017)
• Costa Rica (2018)
• Arizona (2022)
• Florida (2023)
• Belize (2024)
• Costa Rica (2025)
• Summer Ecology Research
• Teacher Resources
• In the planning stages, the limitations of the time and the materials should be assessed, and the potential sources of error should be controlled.
• In the data collection and processing stages, the degree of accuracy of a measuring device should be stated.
• In the evaluation of the investigation, the sources of error should be discussed, along with the possible ways of avoiding them. 
• Error in measurement instrument use and calibration :  for example, if an electronic scale reads 0.05 g too high for all mass measurements because it was improperly tared.
• Faulty measurement equipment :  for example, if a tape measure has been stretched out so everything you measured with it is larger than reality.  
• Faulty use of measurement equipment:  for example, if a researcher consistently reads a graduated cylinder from above (as opposed to directly looking at the meniscus).  
• ​ Sensitivity limits:   because of its measurement uncertainty, an instrument may not be able to respond or indicate a change in a quantity that is too small.  So, only larger measurements are recorded, biasing results towards larger measures.  

• Variation in measurement readings:   for example, if one person reads 27.5 degrees and another person reads 27.8 degrees when taking the temperature of the same solution.  This error can be minimized by taking more data and averaging over a large number of observations.   
• ​ Sample size:   a small sample size is going to increase the uncertainty of the conclusions being drawn.     A small sample size is going to increase the impact of any single error in measurement.  By having a large sample, the impact of any one random error is diluted.
• Background noise:   noise is extraneous disturbances that are unpredictable or random and cannot be completely accounted for.  For example, when taking an ECG measurement, the presence of a cell phone near the monitoring device might effect the measurements.
• Intrinsic variability:  biological material is notably variable from subject to subject or within the same subject over the course of time.  For example, the solute concentration of potato tissue may be calculated by soaking pieces of tissue in a range of concentrations of sucrose solutions. However, different pieces of tissue will vary in their osmolarity especially if they have been taken from different potatoes.  
• Sensitivity limits:   an instrument may not be able to respond or indicate a change in a quantity that is too small or the observer may not notice the change.  For example, the resolution limitations of a microscope may limit an observer from noticing changes in a cell structure.
• The act of measuring:   when a measurement is taken this can affect the environment of the experiment.  For example when a cold thermometer is put in a test tube of warm water, the water will be cooled by the presence of the thermometer. ​ Or, an animal being observed changes it's behavior because of the presence of the researcher in its habitat.
• Measurement uncertainty: every measuring device has a range in which the measurements are accurate.  A researcher may randomly sample on the higher end or lower end of the measurement range, which would decrease precision.
• Experimenter fatigue:   when people have to make a large number of tedious measurements, their concentration spans vary.  Automated measuring, for example through the use of a data logger system, can help reduce the likelihood of this type of error. Alternatively, the experimenter can take a break occasionally.
• Experimenter experience :  novice researchers are more likely to make random errors because they may not have training or experience in observing or measuring.

Understanding Systematic and Random errors

Errors are an inevitable part of any experimental process, and understanding and managing them is crucial for obtaining reliable results. Broadly, errors can be categorized into systematic and random errors. This article serves as an introduction to the concept of errors in experimental design, setting the stage for a deeper exploration of replication, randomization, and blocking.

Types of Errors

Random Errors Random errors arise from unpredictable and uncontrollable variations in the experimental process. These errors can occur due to fluctuations in measurement instruments, environmental changes, or inherent variability in the subjects being studied. For example, slight variations in temperature or humidity during an experiment could cause random errors in the results.

Systematic Errors Systematic errors, on the other hand, are consistent and repeatable errors that occur due to flaws in the experimental setup or procedure. These errors can significantly bias the results and are often harder to detect and correct. Common sources of systematic errors include:

• Instrument Calibration Issues : If an instrument is not calibrated correctly, all measurements taken with it will be consistently off.
• Biased Sampling : When the sample drawn does not represent the population. For example, if a chemical mixture is not stirred properly before taking a sample, the sample might not reflect the true composition of the mixture.
• Procedural Flaws : Consistently incorrect application of a procedure across all experimental units.

Impact of Errors on Experimental Results

Accuracy vs. Precision Accuracy refers to how close the experimental results are to the true value, while precision denotes how reproducible the results are. Random errors typically affect precision, making the results more variable, whereas systematic errors affect accuracy, causing a consistent deviation from the true value.

Bias and Variability Errors contribute to both bias and variability in experimental outcomes. Bias results from systematic errors, leading to consistently skewed results. Variability, influenced by random errors, results in a spread of values around the true measurement.

Error Management

First, you need to identify all potential sources of errors. Make a list of all the variables that could affect your experiment. Let us say you would like to determine factors that affect the pot life of a coating system. The pot life of a coating system refers to the amount of time you have to use the mixed coating material before it starts to harden and becomes unusable. Variables that could affect the reproducibility of the measurements include:

Random Errors

• Environmental Fluctuations : Slight changes in temperature or humidity during the pot life measurement.
• Instrumental Variations : Minor, unavoidable fluctuations in the performance of the measuring instruments.
• Human Error : Accidental deviations in following procedures, such as slightly different stirring times or weighing errors.

Systematic Errors

• Instrument Calibration Issues : If the device used for measuring pot life is not accurately calibrated, all measurements will be consistently incorrect.
• Consistent Environmental Conditions : If the temperature or humidity in the testing environment is not controlled, it could systematically affect the pot life. For example, if you take measurements on two consecutive days, and one day is rainy while the other is hot, the pot life measurements taken on the hot day will be shorter due to the increased reaction rates that come with higher temperatures.
• Inconsistent Procedures : Using inconsistent mixing procedures or tools that introduce a systematic bias, such as always mixing for too short or too long.
• Material Consistency : Variations in the batch quality of the coating materials.

There is no way to eliminate all these sources of errors but there are ways to deal with them, minimizing there impact and still recording high quality results.

Strategies for Error Management

In addition to a maintenance and calibration schedule and developing test procedures that are as accurate as possible, there is another key principle when it comes to error management: “Block what you can and randomize what you can’t.”

This principle emphasizes the importance of controlling for known sources of variability (blocking) and using randomization to mitigate the impact of unknown or uncontrollable factors.

In fact, there are 3 key principles in DoE. Blocking, randomization and replication. We take a look at those in more detail in the next blog post.

Replication, Randomization and Blocking in DoE

Advanced doe plans (part 1).

Types of Error — Overview & Comparison - Expii

Types of error — overview & comparison, explanations (3), types of error.

• Errors are common occurrences in chemistry and there are three specific types of errors that may occur during experiments.

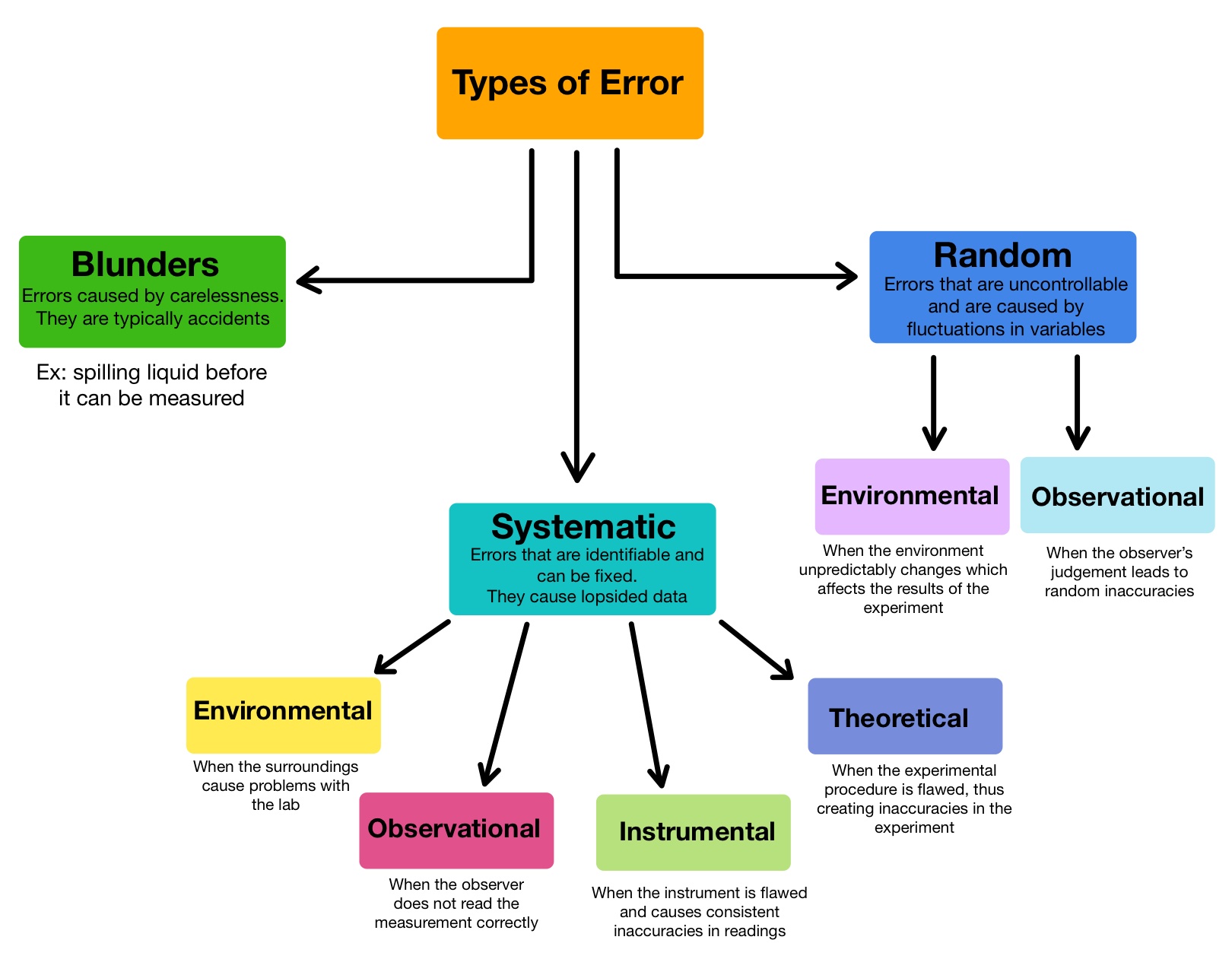
Image source: Caroline Monahan

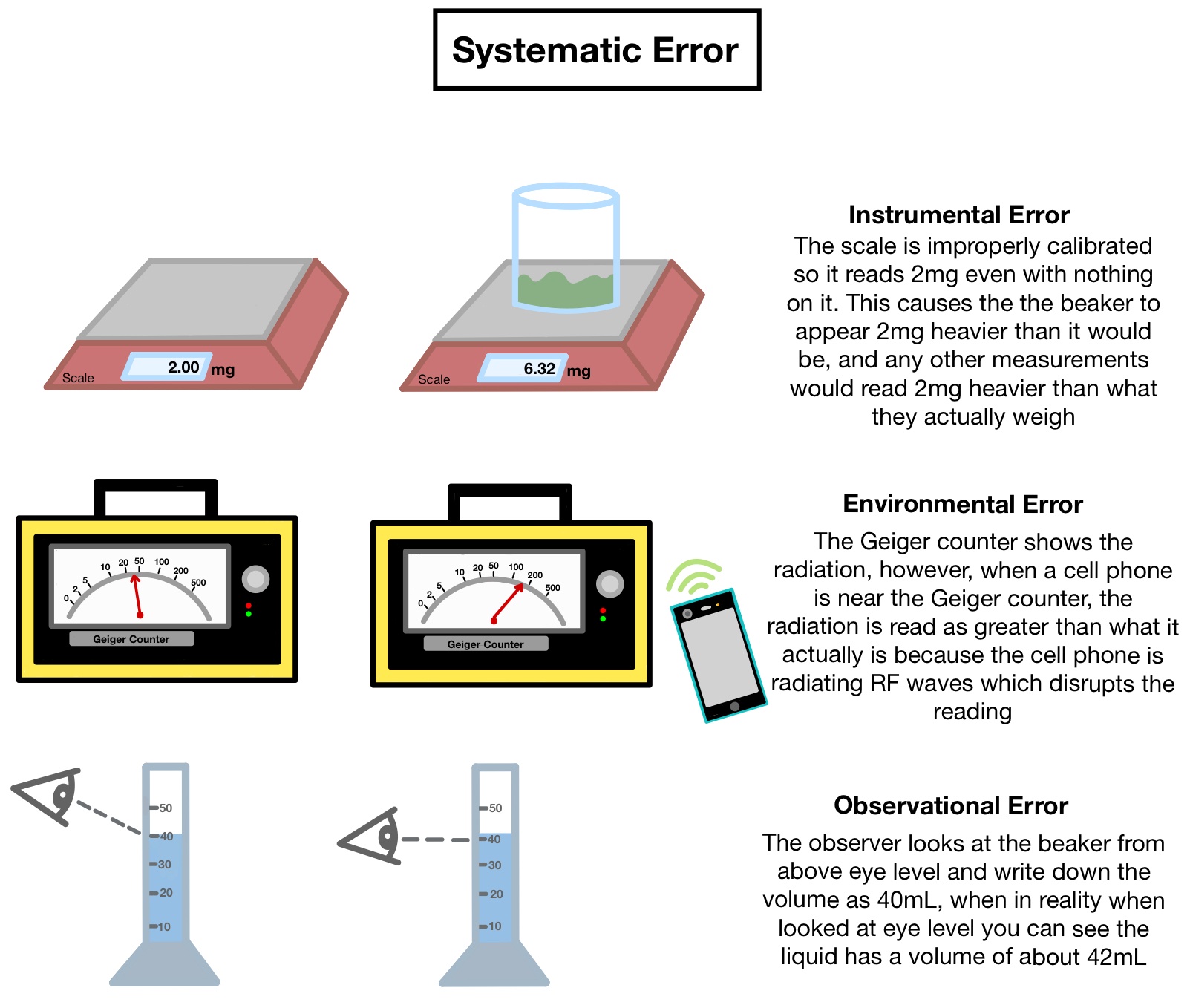
Systematic Errors:

Systematic errors are errors that have a clear cause and can be eliminated for future experiments

There are four different types of systematic errors:

Instrumental: When the instrument being used does not function properly causing error in the experiment (such as a scale that reads 2g more than the actual weight of the object, causing the measured values to read too high consistently )

Environmental: When the surrounding environment (such as a lab) causes errors in the experiment (the scientist cell phone's RF waves cause the geiger counters to incorrectly display the radiation)

Observational: When the scientist inaccurately reads a measurement wrong (such as when not standing straight-on when reading the volume of a flask causing the volume to be incorrectly measured)

Theoretical: When the model system being used causes the results to be inaccurate (such as being told that humidity does not affect the results of an experiment when it actually does)

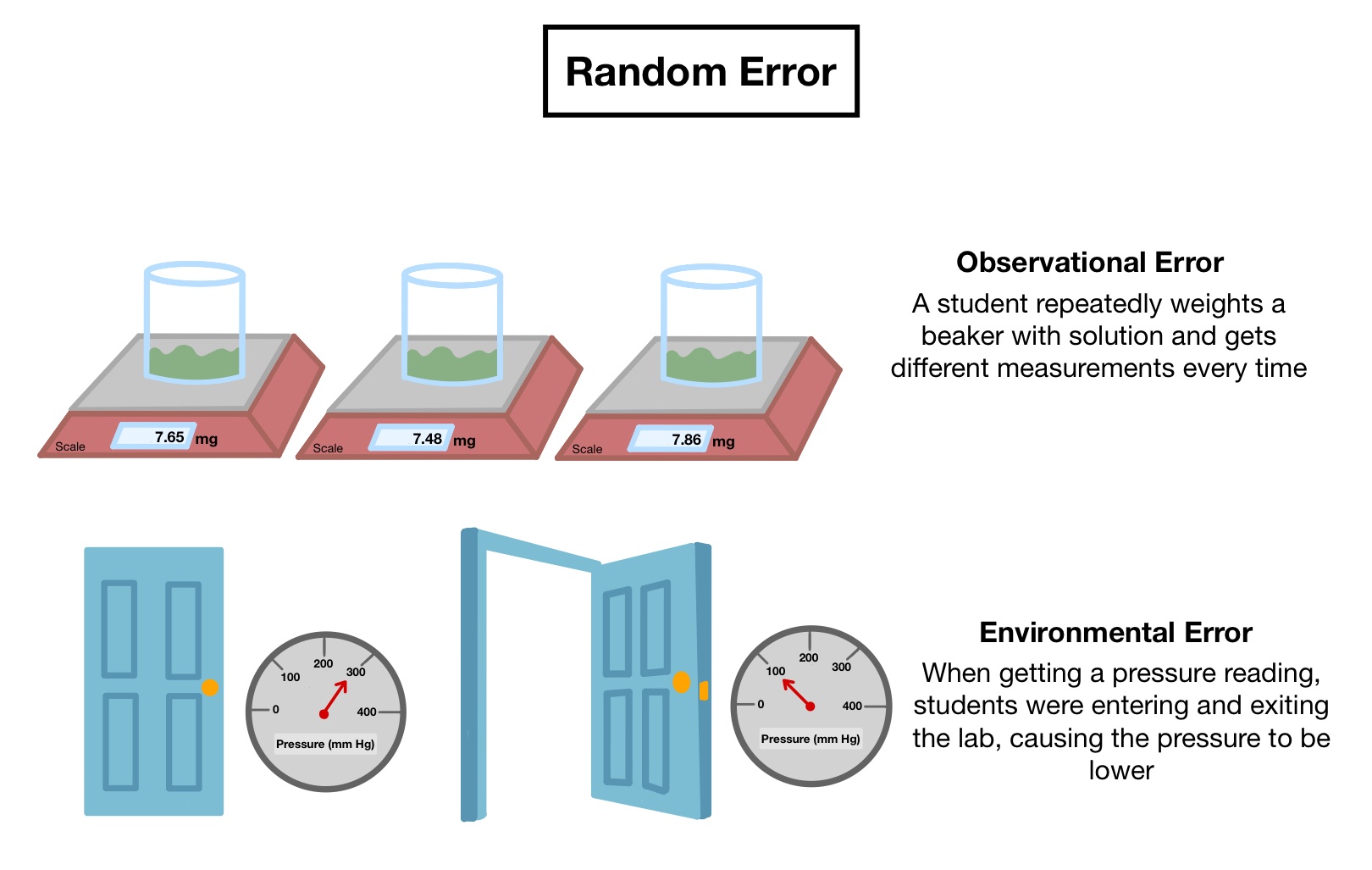
Random Errors:

Random errors occur randomly, and sometimes have no source/cause

There are two types of random errors

Observational: When the observer makes consistent observational mistakes (such not reading the scale correctly and writing down values that are constantly too low or too high)

Environmental : When unpredictable changes occur in the environment of the experiment (such as students repeatedly opening and closing the door when the pressure is being measured, causing fluctuations in the reading)

Systematic vs. Random Errors

• Systematic errors and random errors are sometimes similar, so here is a way to distinguish between them:

Systematic Errors are errors that occur in the same direction consistently, meaning that if the scale was off by and extra 3lbs, then every measurement for that experiment would contain an extra 3 lbs. This error is identifiable and, once identified, they can be eliminated for future experiments

Random Errors are errors that can occur in any direction and are not consistent, thus they are hard to identify and thus the error is harder to fix for future experiments. An observer might make a mistake when measuring and record a value that's too low, but because no one else was there when it was measured, the mistake went on unnoticed.

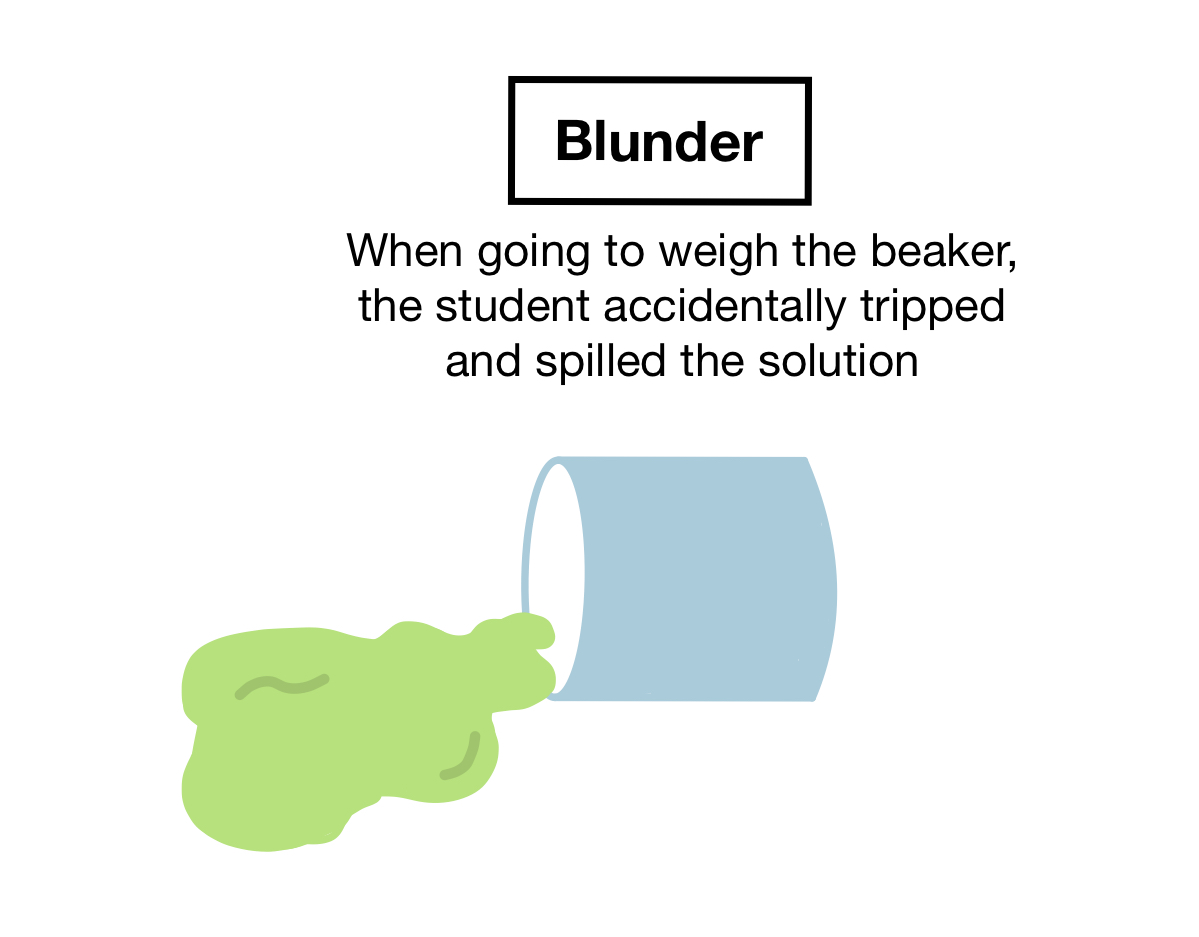
Blunders are simply a clear mistake that causes an error in the experiment

Example: such as dropping a beaker with the solution before measuring the final mass

Related Lessons

Whenever we do an experiment, we have to consider errors in our measurements . Errors are the difference between the true measurement and what we measured. We show our error by writing our measurement with an uncertainty . There are three types of errors: systematic, random, and human error.

Systematic Error

Systematic errors come from identifiable sources. The results caused by systematic errors will always be either too high or too low. For example, an uncalibrated scale might always read the mass of an object as 0.5g too high. Because systematic errors are consistent, you can often fix them. There are four types of systematic error: observational, instrumental, environmental, and theoretical.

Observational errors occur when you make an incorrect observation. For example, you might misread an instrument.

Instrumental errors happen when an instrument gives the wrong reading. Most often, you can fix instrumental errors by recalibrating the instrument.

Environmental errors are a result of the laboratory environment. For example, when I was in college, our chemistry lab had one scale that was under a vent. Every time the vent was blowing the scale would read too high. We all learned to avoid that scale.

Theoretical errors arise because of the experimental procedure or assumptions. For example, we assume that air pressure does not affect our results but it does.

Random Error

Random errors are the result of unpredictable changes. Unlike systematic errors, random errors will cause varying results. One moment a reading might be too high and the next moment the reading is too low. You can account for random errors by repeating your measurements. Taking repeated measurements allows you to use statistics to calculate the random error. There are two types of random error: observational and environmental.

Random observational errors are not predictable. They fluctuate between being too high or too low. An example would be an instrument's reading fluctuating. If you were to take the mid-point of the fluctuations, you may be too high on one measurement but too low on the next.

Environmental errors are caused by the laboratory environment. An example might be a malfunctioning instrument. In my freshman chemistry lab, I had a pH meter that would not stay calibrated. After five minutes the pH values would fluctuate unpredictably.

Human Error

Human errors are a nice way of saying carelessness. For example, a scale might read 21g but, you write down 12g. You want to avoid human errors because they are your fault. Most teachers have no sympathy for carelessness.

(Video) Type I error vs Type II error

By: 365 Data Science

When a hypothesis is tested, errors can occur called type I and type II errors. A type I hypothesis involves rejecting the true null hypothesis or gives a false positive. Type II occurs when a false null hypothesis is accepted or gives a false negative. The type II error is a less serious error since it can happen with hard to test data.

An example is given with you liking another person. The hypothesis is that that person likes you back. Type I error occurs if you do not ask out the other person and assume they don't like you. Type II error occurs when you ask out the other person, but they reject you.

A chart is used to summarize the types of error.