two tailed hypothesis t test

Search Search Please fill out this field.

What Is a Two-Tailed Test?

Understanding a two-tailed test, special considerations, two-tailed vs. one-tailed test.

Two-Tailed Test FAQs
Corporate Finance
Financial Analysis

What Is a Two-Tailed Test? Definition and Example

Adam Hayes, Ph.D., CFA, is a financial writer with 15+ years Wall Street experience as a derivatives trader. Besides his extensive derivative trading expertise, Adam is an expert in economics and behavioral finance. Adam received his master's in economics from The New School for Social Research and his Ph.D. from the University of Wisconsin-Madison in sociology. He is a CFA charterholder as well as holding FINRA Series 7, 55 & 63 licenses. He currently researches and teaches economic sociology and the social studies of finance at the Hebrew University in Jerusalem.

Investopedia / Joules Garcia

A two-tailed test, in statistics, is a method in which the critical area of a distribution is two-sided and tests whether a sample is greater than or less than a certain range of values. It is used in null-hypothesis testing and testing for statistical significance . If the sample being tested falls into either of the critical areas, the alternative hypothesis is accepted instead of the null hypothesis.

Key Takeaways

In statistics, a two-tailed test is a method in which the critical area of a distribution is two-sided and tests whether a sample is greater or less than a range of values.
It is used in null-hypothesis testing and testing for statistical significance.
If the sample being tested falls into either of the critical areas, the alternative hypothesis is accepted instead of the null hypothesis.
By convention two-tailed tests are used to determine significance at the 5% level, meaning each side of the distribution is cut at 2.5%.

A basic concept of inferential statistics is hypothesis testing , which determines whether a claim is true or not given a population parameter. A hypothesis test that is designed to show whether the mean of a sample is significantly greater than and significantly less than the mean of a population is referred to as a two-tailed test. The two-tailed test gets its name from testing the area under both tails of a normal distribution , although the test can be used in other non-normal distributions.

A two-tailed test is designed to examine both sides of a specified data range as designated by the probability distribution involved. The probability distribution should represent the likelihood of a specified outcome based on predetermined standards. This requires the setting of a limit designating the highest (or upper) and lowest (or lower) accepted variable values included within the range. Any data point that exists above the upper limit or below the lower limit is considered out of the acceptance range and in an area referred to as the rejection range.

There is no inherent standard about the number of data points that must exist within the acceptance range. In instances where precision is required, such as in the creation of pharmaceutical drugs, a rejection rate of 0.001% or less may be instituted. In instances where precision is less critical, such as the number of food items in a product bag, a rejection rate of 5% may be appropriate.

A two-tailed test can also be used practically during certain production activities in a firm, such as with the production and packaging of candy at a particular facility. If the production facility designates 50 candies per bag as its goal, with an acceptable distribution of 45 to 55 candies, any bag found with an amount below 45 or above 55 is considered within the rejection range.

To confirm the packaging mechanisms are properly calibrated to meet the expected output, random sampling may be taken to confirm accuracy. A simple random sample takes a small, random portion of the entire population to represent the entire data set, where each member has an equal probability of being chosen.

For the packaging mechanisms to be considered accurate, an average of 50 candies per bag with an appropriate distribution is desired. Additionally, the number of bags that fall within the rejection range needs to fall within the probability distribution limit considered acceptable as an error rate. Here, the null hypothesis would be that the mean is 50 while the alternate hypothesis would be that it is not 50.

If, after conducting the two-tailed test, the z-score falls in the rejection region, meaning that the deviation is too far from the desired mean, then adjustments to the facility or associated equipment may be required to correct the error. Regular use of two-tailed testing methods can help ensure production stays within limits over the long term.

Be careful to note if a statistical test is one- or two-tailed as this will greatly influence a model's interpretation.

When a hypothesis test is set up to show that the sample mean would be only higher than the population mean, this is referred to as a one-tailed test . A formulation of this hypothesis would be, for example, that "the returns on an investment fund would be at least x%." One-tailed tests could also be set up to show that the sample mean could be only less than the population mean. The key difference from a two-tailed test is that in a two-tailed test, the sample mean could be different from the population mean by being either higher or lower than it.

If the sample being tested falls into the one-sided critical area, the alternative hypothesis will be accepted instead of the null hypothesis. A one-tailed test is also known as a directional hypothesis or directional test.

A two-tailed test, on the other hand, is designed to examine both sides of a specified data range to test whether a sample is greater than or less than the range of values.

Example of a Two-Tailed Test

As a hypothetical example, imagine that a new stockbroker , named XYZ, claims that their brokerage fees are lower than that of your current stockbroker, ABC) Data available from an independent research firm indicates that the mean and standard deviation of all ABC broker clients are $18 and $6, respectively.

A sample of 100 clients of ABC is taken, and brokerage charges are calculated with the new rates of XYZ broker. If the mean of the sample is $18.75 and the sample standard deviation is $6, can any inference be made about the difference in the average brokerage bill between ABC and XYZ broker?

H 0 : Null Hypothesis: mean = 18
H 1 : Alternative Hypothesis: mean <> 18 (This is what we want to prove.)
Rejection region: Z <= - Z 2.5 and Z>=Z 2.5 (assuming 5% significance level, split 2.5 each on either side).
Z = (sample mean – mean) / (std-dev / sqrt (no. of samples)) = (18.75 – 18) / (6/(sqrt(100)) = 1.25

This calculated Z value falls between the two limits defined by: - Z 2.5 = -1.96 and Z 2.5 = 1.96.

This concludes that there is insufficient evidence to infer that there is any difference between the rates of your existing broker and the new broker. Therefore, the null hypothesis cannot be rejected. Alternatively, the p-value = P(Z< -1.25)+P(Z >1.25) = 2 * 0.1056 = 0.2112 = 21.12%, which is greater than 0.05 or 5%, leads to the same conclusion.

How Is a Two-Tailed Test Designed?

A two-tailed test is designed to determine whether a claim is true or not given a population parameter. It examines both sides of a specified data range as designated by the probability distribution involved. As such, the probability distribution should represent the likelihood of a specified outcome based on predetermined standards.

What Is the Difference Between a Two-Tailed and One-Tailed Test?

A two-tailed hypothesis test is designed to show whether the sample mean is significantly greater than or significantly less than the mean of a population. The two-tailed test gets its name from testing the area under both tails (sides) of a normal distribution. A one-tailed hypothesis test, on the other hand, is set up to show only one test; that the sample mean would be higher than the population mean, or, in a separate test, that the sample mean would be lower than the population mean.

What Is a Z-score?

A Z-score numerically describes a value's relationship to the mean of a group of values and is measured in terms of the number of standard deviations from the mean. If a Z-score is 0, it indicates that the data point's score is identical to the mean score whereas Z-scores of 1.0 and -1.0 would indicate values one standard deviation above or below the mean. In most large data sets, 99% of values have a Z-score between -3 and 3, meaning they lie within three standard deviations above and below the mean.

San Jose State University. " 6: Introduction to Null Hypothesis Significance Testing ."

Terms of Service
Editorial Policy
Privacy Policy
Your Privacy Choices

t-test Calculator

Table of contents

Welcome to our t-test calculator! Here you can not only easily perform one-sample t-tests , but also two-sample t-tests , as well as paired t-tests .

Do you prefer to find the p-value from t-test, or would you rather find the t-test critical values? Well, this t-test calculator can do both! 😊

What does a t-test tell you? Take a look at the text below, where we explain what actually gets tested when various types of t-tests are performed. Also, we explain when to use t-tests (in particular, whether to use the z-test vs. t-test) and what assumptions your data should satisfy for the results of a t-test to be valid. If you've ever wanted to know how to do a t-test by hand, we provide the necessary t-test formula, as well as tell you how to determine the number of degrees of freedom in a t-test.

When to use a t-test?

A t-test is one of the most popular statistical tests for location , i.e., it deals with the population(s) mean value(s).

There are different types of t-tests that you can perform:

A one-sample t-test;
A two-sample t-test; and
A paired t-test.

In the next section , we explain when to use which. Remember that a t-test can only be used for one or two groups . If you need to compare three (or more) means, use the analysis of variance ( ANOVA ) method.

The t-test is a parametric test, meaning that your data has to fulfill some assumptions :

The data points are independent; AND
The data, at least approximately, follow a normal distribution .

If your sample doesn't fit these assumptions, you can resort to nonparametric alternatives. Visit our Mann–Whitney U test calculator or the Wilcoxon rank-sum test calculator to learn more. Other possibilities include the Wilcoxon signed-rank test or the sign test.

Which t-test?

Your choice of t-test depends on whether you are studying one group or two groups:

One sample t-test

Choose the one-sample t-test to check if the mean of a population is equal to some pre-set hypothesized value .

The average volume of a drink sold in 0.33 l cans — is it really equal to 330 ml?

The average weight of people from a specific city — is it different from the national average?

Two-sample t-test

Choose the two-sample t-test to check if the difference between the means of two populations is equal to some pre-determined value when the two samples have been chosen independently of each other.

In particular, you can use this test to check whether the two groups are different from one another .

The average difference in weight gain in two groups of people: one group was on a high-carb diet and the other on a high-fat diet.

The average difference in the results of a math test from students at two different universities.

This test is sometimes referred to as an independent samples t-test , or an unpaired samples t-test .

Paired t-test

A paired t-test is used to investigate the change in the mean of a population before and after some experimental intervention , based on a paired sample, i.e., when each subject has been measured twice: before and after treatment.

In particular, you can use this test to check whether, on average, the treatment has had any effect on the population .

The change in student test performance before and after taking a course.

The change in blood pressure in patients before and after administering some drug.

How to do a t-test?

So, you've decided which t-test to perform. These next steps will tell you how to calculate the p-value from t-test or its critical values, and then which decision to make about the null hypothesis.

Decide on the alternative hypothesis :

Use a two-tailed t-test if you only care whether the population's mean (or, in the case of two populations, the difference between the populations' means) agrees or disagrees with the pre-set value.

Use a one-tailed t-test if you want to test whether this mean (or difference in means) is greater/less than the pre-set value.

Compute your T-score value :

Formulas for the test statistic in t-tests include the sample size , as well as its mean and standard deviation . The exact formula depends on the t-test type — check the sections dedicated to each particular test for more details.

Determine the degrees of freedom for the t-test:

The degrees of freedom are the number of observations in a sample that are free to vary as we estimate statistical parameters. In the simplest case, the number of degrees of freedom equals your sample size minus the number of parameters you need to estimate . Again, the exact formula depends on the t-test you want to perform — check the sections below for details.

The degrees of freedom are essential, as they determine the distribution followed by your T-score (under the null hypothesis). If there are d degrees of freedom, then the distribution of the test statistics is the t-Student distribution with d degrees of freedom . This distribution has a shape similar to N(0,1) (bell-shaped and symmetric) but has heavier tails . If the number of degrees of freedom is large (>30), which generically happens for large samples, the t-Student distribution is practically indistinguishable from N(0,1).

💡 The t-Student distribution owes its name to William Sealy Gosset, who, in 1908, published his paper on the t-test under the pseudonym "Student". Gosset worked at the famous Guinness Brewery in Dublin, Ireland, and devised the t-test as an economical way to monitor the quality of beer. Cheers! 🍺🍺🍺

p-value from t-test

Recall that the p-value is the probability (calculated under the assumption that the null hypothesis is true) that the test statistic will produce values at least as extreme as the T-score produced for your sample . As probabilities correspond to areas under the density function, p-value from t-test can be nicely illustrated with the help of the following pictures:

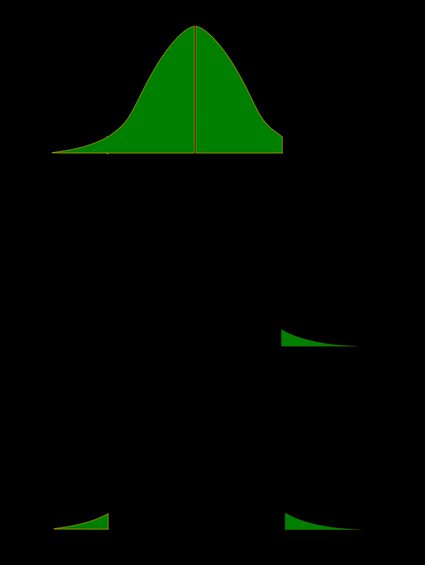
The following formulae say how to calculate p-value from t-test. By cdf t,d we denote the cumulative distribution function of the t-Student distribution with d degrees of freedom:

p-value from left-tailed t-test:

p-value = cdf t,d (t score )

p-value from right-tailed t-test:

p-value = 1 − cdf t,d (t score )

p-value from two-tailed t-test:

p-value = 2 × cdf t,d (−|t score |)

or, equivalently: p-value = 2 − 2 × cdf t,d (|t score |)

However, the cdf of the t-distribution is given by a somewhat complicated formula. To find the p-value by hand, you would need to resort to statistical tables, where approximate cdf values are collected, or to specialized statistical software. Fortunately, our t-test calculator determines the p-value from t-test for you in the blink of an eye!

t-test critical values

Recall, that in the critical values approach to hypothesis testing, you need to set a significance level, α, before computing the critical values , which in turn give rise to critical regions (a.k.a. rejection regions).

Formulas for critical values employ the quantile function of t-distribution, i.e., the inverse of the cdf :

Critical value for left-tailed t-test: cdf t,d -1 (α)

critical region:

(-∞, cdf t,d -1 (α)]

Critical value for right-tailed t-test: cdf t,d -1 (1-α)

[cdf t,d -1 (1-α), ∞)

Critical values for two-tailed t-test: ±cdf t,d -1 (1-α/2)

(-∞, -cdf t,d -1 (1-α/2)] ∪ [cdf t,d -1 (1-α/2), ∞)

To decide the fate of the null hypothesis, just check if your T-score lies within the critical region:

If your T-score belongs to the critical region , reject the null hypothesis and accept the alternative hypothesis.

If your T-score is outside the critical region , then you don't have enough evidence to reject the null hypothesis.

How to use our t-test calculator

Choose the type of t-test you wish to perform:

A one-sample t-test (to test the mean of a single group against a hypothesized mean);

A two-sample t-test (to compare the means for two groups); or

A paired t-test (to check how the mean from the same group changes after some intervention).

Two-tailed;

Left-tailed; or

Right-tailed.

This t-test calculator allows you to use either the p-value approach or the critical regions approach to hypothesis testing!

Enter your T-score and the number of degrees of freedom . If you don't know them, provide some data about your sample(s): sample size, mean, and standard deviation, and our t-test calculator will compute the T-score and degrees of freedom for you .

Once all the parameters are present, the p-value, or critical region, will immediately appear underneath the t-test calculator, along with an interpretation!

One-sample t-test

The null hypothesis is that the population mean is equal to some value μ 0 \mu_0 μ 0 .

The alternative hypothesis is that the population mean is:

different from μ 0 \mu_0 μ 0 ;
smaller than μ 0 \mu_0 μ 0 ; or
greater than μ 0 \mu_0 μ 0 .

One-sample t-test formula :

μ 0 \mu_0 μ 0 — Mean postulated in the null hypothesis;
n n n — Sample size;
x ˉ \bar{x} x ˉ — Sample mean; and
s s s — Sample standard deviation.

Number of degrees of freedom in t-test (one-sample) = n − 1 n-1 n − 1 .

The null hypothesis is that the actual difference between these groups' means, μ 1 \mu_1 μ 1 , and μ 2 \mu_2 μ 2 , is equal to some pre-set value, Δ \Delta Δ .

The alternative hypothesis is that the difference μ 1 − μ 2 \mu_1 - \mu_2 μ 1 − μ 2 is:

Different from Δ \Delta Δ ;
Smaller than Δ \Delta Δ ; or
Greater than Δ \Delta Δ .

In particular, if this pre-determined difference is zero ( Δ = 0 \Delta = 0 Δ = 0 ):

The null hypothesis is that the population means are equal.

The alternate hypothesis is that the population means are:

μ 1 \mu_1 μ 1 and μ 2 \mu_2 μ 2 are different from one another;
μ 1 \mu_1 μ 1 is smaller than μ 2 \mu_2 μ 2 ; and
μ 1 \mu_1 μ 1 is greater than μ 2 \mu_2 μ 2 .

Formally, to perform a t-test, we should additionally assume that the variances of the two populations are equal (this assumption is called the homogeneity of variance ).

There is a version of a t-test that can be applied without the assumption of homogeneity of variance: it is called a Welch's t-test . For your convenience, we describe both versions.

Two-sample t-test if variances are equal

Use this test if you know that the two populations' variances are the same (or very similar).

Two-sample t-test formula (with equal variances) :

where s p s_p s p is the so-called pooled standard deviation , which we compute as:

Δ \Delta Δ — Mean difference postulated in the null hypothesis;
n 1 n_1 n 1 — First sample size;
x ˉ 1 \bar{x}_1 x ˉ 1 — Mean for the first sample;
s 1 s_1 s 1 — Standard deviation in the first sample;
n 2 n_2 n 2 — Second sample size;
x ˉ 2 \bar{x}_2 x ˉ 2 — Mean for the second sample; and
s 2 s_2 s 2 — Standard deviation in the second sample.

Number of degrees of freedom in t-test (two samples, equal variances) = n 1 + n 2 − 2 n_1 + n_2 - 2 n 1 + n 2 − 2 .

Two-sample t-test if variances are unequal (Welch's t-test)

Use this test if the variances of your populations are different.

Two-sample Welch's t-test formula if variances are unequal:

s 1 s_1 s 1 — Standard deviation in the first sample;
s 2 s_2 s 2 — Standard deviation in the second sample.

The number of degrees of freedom in a Welch's t-test (two-sample t-test with unequal variances) is very difficult to count. We can approximate it with the help of the following Satterthwaite formula :

Alternatively, you can take the smaller of n 1 − 1 n_1 - 1 n 1 − 1 and n 2 − 1 n_2 - 1 n 2 − 1 as a conservative estimate for the number of degrees of freedom.

🔎 The Satterthwaite formula for the degrees of freedom can be rewritten as a scaled weighted harmonic mean of the degrees of freedom of the respective samples: n 1 − 1 n_1 - 1 n 1 − 1 and n 2 − 1 n_2 - 1 n 2 − 1 , and the weights are proportional to the standard deviations of the corresponding samples.

As we commonly perform a paired t-test when we have data about the same subjects measured twice (before and after some treatment), let us adopt the convention of referring to the samples as the pre-group and post-group.

The null hypothesis is that the true difference between the means of pre- and post-populations is equal to some pre-set value, Δ \Delta Δ .

The alternative hypothesis is that the actual difference between these means is:

Typically, this pre-determined difference is zero. We can then reformulate the hypotheses as follows:

The null hypothesis is that the pre- and post-means are the same, i.e., the treatment has no impact on the population .

The alternative hypothesis:

The pre- and post-means are different from one another (treatment has some effect);
The pre-mean is smaller than the post-mean (treatment increases the result); or
The pre-mean is greater than the post-mean (treatment decreases the result).

Paired t-test formula

In fact, a paired t-test is technically the same as a one-sample t-test! Let us see why it is so. Let x 1 , . . . , x n x_1, ... , x_n x 1 , ... , x n be the pre observations and y 1 , . . . , y n y_1, ... , y_n y 1 , ... , y n the respective post observations. That is, x i , y i x_i, y_i x i , y i are the before and after measurements of the i -th subject.

For each subject, compute the difference, d i : = x i − y i d_i := x_i - y_i d i := x i − y i . All that happens next is just a one-sample t-test performed on the sample of differences d 1 , . . . , d n d_1, ... , d_n d 1 , ... , d n . Take a look at the formula for the T-score :

Δ \Delta Δ — Mean difference postulated in the null hypothesis;

n n n — Size of the sample of differences, i.e., the number of pairs;

x ˉ \bar{x} x ˉ — Mean of the sample of differences; and

s s s — Standard deviation of the sample of differences.

Number of degrees of freedom in t-test (paired): n − 1 n - 1 n − 1

t-test vs Z-test

We use a Z-test when we want to test the population mean of a normally distributed dataset, which has a known population variance . If the number of degrees of freedom is large, then the t-Student distribution is very close to N(0,1).

Hence, if there are many data points (at least 30), you may swap a t-test for a Z-test, and the results will be almost identical. However, for small samples with unknown variance, remember to use the t-test because, in such cases, the t-Student distribution differs significantly from the N(0,1)!

🙋 Have you concluded you need to perform the z-test? Head straight to our z-test calculator !

What is a t-test?

A t-test is a widely used statistical test that analyzes the means of one or two groups of data. For instance, a t-test is performed on medical data to determine whether a new drug really helps.

What are different types of t-tests?

Different types of t-tests are:

One-sample t-test;
Two-sample t-test; and
Paired t-test.

How to find the t value in a one sample t-test?

To find the t-value:

Subtract the null hypothesis mean from the sample mean value.
Divide the difference by the standard deviation of the sample.
Multiply the resultant with the square root of the sample size.

.css-m482sy.css-m482sy{color:#2B3148;background-color:transparent;font-family:var(--calculator-ui-font-family),Verdana,sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-m482sy.css-m482sy:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-m482sy .js-external-link-button.link-like,.css-m482sy .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-m482sy .js-external-link-button.link-like:hover,.css-m482sy .js-external-link-anchor:hover,.css-m482sy .js-external-link-button.link-like:active,.css-m482sy .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-m482sy .js-external-link-button.link-like:focus-visible,.css-m482sy .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-m482sy p,.css-m482sy div{margin:0;display:block;}.css-m482sy pre{margin:0;display:block;}.css-m482sy pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-m482sy pre:not(:first-child){padding-top:8px;}.css-m482sy ul,.css-m482sy ol{display:block margin:0;padding-left:20px;}.css-m482sy ul li,.css-m482sy ol li{padding-top:8px;}.css-m482sy ul ul,.css-m482sy ol ul,.css-m482sy ul ol,.css-m482sy ol ol{padding-top:0;}.css-m482sy ul:not(:first-child),.css-m482sy ol:not(:first-child){padding-top:4px;} .css-1h42f0z{margin:auto;overflow:auto;overflow-wrap:break-word;word-break:break-word;}@font-face{font-family:'KaTeX_AMS';src:url(/katex-fonts/KaTeX_AMS-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_AMS-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_AMS-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Script';src:url(/katex-fonts/KaTeX_Script-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Script-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Script-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size1';src:url(/katex-fonts/KaTeX_Size1-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size1-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size1-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size2';src:url(/katex-fonts/KaTeX_Size2-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size2-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size2-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size3';src:url(/katex-fonts/KaTeX_Size3-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size3-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size3-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size4';src:url(/katex-fonts/KaTeX_Size4-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size4-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size4-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Typewriter';src:url(/katex-fonts/KaTeX_Typewriter-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Typewriter-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Typewriter-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}.css-1h42f0z .katex{font:normal 1.21em KaTeX_Main,Times New Roman,serif;line-height:1.2;text-indent:0;text-rendering:auto;}.css-1h42f0z .katex *{-ms-high-contrast-adjust:none!important;border-color:currentColor;}.css-1h42f0z .katex .katex-version::after{content:'0.13.13';}.css-1h42f0z .katex .katex-mathml{position:absolute;clip:rect(1px,1px,1px,1px);padding:0;border:0;height:1px;width:1px;overflow:hidden;}.css-1h42f0z .katex .katex-html>.newline{display:block;}.css-1h42f0z .katex .base{position:relative;display:inline-block;white-space:nowrap;width:-webkit-min-content;width:-moz-min-content;width:-webkit-min-content;width:-moz-min-content;width:min-content;}.css-1h42f0z .katex .strut{display:inline-block;}.css-1h42f0z .katex .textbf{font-weight:bold;}.css-1h42f0z .katex .textit{font-style:italic;}.css-1h42f0z .katex .textrm{font-family:KaTeX_Main;}.css-1h42f0z .katex .textsf{font-family:KaTeX_SansSerif;}.css-1h42f0z .katex .texttt{font-family:KaTeX_Typewriter;}.css-1h42f0z .katex .mathnormal{font-family:KaTeX_Math;font-style:italic;}.css-1h42f0z .katex .mathit{font-family:KaTeX_Main;font-style:italic;}.css-1h42f0z .katex .mathrm{font-style:normal;}.css-1h42f0z .katex .mathbf{font-family:KaTeX_Main;font-weight:bold;}.css-1h42f0z .katex .boldsymbol{font-family:KaTeX_Math;font-weight:bold;font-style:italic;}.css-1h42f0z .katex .amsrm{font-family:KaTeX_AMS;}.css-1h42f0z .katex .mathbb,.css-1h42f0z .katex .textbb{font-family:KaTeX_AMS;}.css-1h42f0z .katex .mathcal{font-family:KaTeX_Caligraphic;}.css-1h42f0z .katex .mathfrak,.css-1h42f0z .katex .textfrak{font-family:KaTeX_Fraktur;}.css-1h42f0z .katex .mathtt{font-family:KaTeX_Typewriter;}.css-1h42f0z .katex .mathscr,.css-1h42f0z .katex .textscr{font-family:KaTeX_Script;}.css-1h42f0z .katex .mathsf,.css-1h42f0z .katex .textsf{font-family:KaTeX_SansSerif;}.css-1h42f0z .katex .mathboldsf,.css-1h42f0z .katex .textboldsf{font-family:KaTeX_SansSerif;font-weight:bold;}.css-1h42f0z .katex .mathitsf,.css-1h42f0z .katex .textitsf{font-family:KaTeX_SansSerif;font-style:italic;}.css-1h42f0z .katex .mainrm{font-family:KaTeX_Main;font-style:normal;}.css-1h42f0z .katex .vlist-t{display:inline-table;table-layout:fixed;border-collapse:collapse;}.css-1h42f0z .katex .vlist-r{display:table-row;}.css-1h42f0z .katex .vlist{display:table-cell;vertical-align:bottom;position:relative;}.css-1h42f0z .katex .vlist>span{display:block;height:0;position:relative;}.css-1h42f0z .katex .vlist>span>span{display:inline-block;}.css-1h42f0z .katex .vlist>span>.pstrut{overflow:hidden;width:0;}.css-1h42f0z .katex .vlist-t2{margin-right:-2px;}.css-1h42f0z .katex .vlist-s{display:table-cell;vertical-align:bottom;font-size:1px;width:2px;min-width:2px;}.css-1h42f0z .katex .vbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:column;-ms-flex-direction:column;flex-direction:column;-webkit-align-items:baseline;-webkit-box-align:baseline;-ms-flex-align:baseline;align-items:baseline;}.css-1h42f0z .katex .hbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:100%;}.css-1h42f0z .katex .thinbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:0;max-width:0;}.css-1h42f0z .katex .msupsub{text-align:left;}.css-1h42f0z .katex .mfrac>span>span{text-align:center;}.css-1h42f0z .katex .mfrac .frac-line{display:inline-block;width:100%;border-bottom-style:solid;}.css-1h42f0z .katex .mfrac .frac-line,.css-1h42f0z .katex .overline .overline-line,.css-1h42f0z .katex .underline .underline-line,.css-1h42f0z .katex .hline,.css-1h42f0z .katex .hdashline,.css-1h42f0z .katex .rule{min-height:1px;}.css-1h42f0z .katex .mspace{display:inline-block;}.css-1h42f0z .katex .llap,.css-1h42f0z .katex .rlap,.css-1h42f0z .katex .clap{width:0;position:relative;}.css-1h42f0z .katex .llap>.inner,.css-1h42f0z .katex .rlap>.inner,.css-1h42f0z .katex .clap>.inner{position:absolute;}.css-1h42f0z .katex .llap>.fix,.css-1h42f0z .katex .rlap>.fix,.css-1h42f0z .katex .clap>.fix{display:inline-block;}.css-1h42f0z .katex .llap>.inner{right:0;}.css-1h42f0z .katex .rlap>.inner,.css-1h42f0z .katex .clap>.inner{left:0;}.css-1h42f0z .katex .clap>.inner>span{margin-left:-50%;margin-right:50%;}.css-1h42f0z .katex .rule{display:inline-block;border:solid 0;position:relative;}.css-1h42f0z .katex .overline .overline-line,.css-1h42f0z .katex .underline .underline-line,.css-1h42f0z .katex .hline{display:inline-block;width:100%;border-bottom-style:solid;}.css-1h42f0z .katex .hdashline{display:inline-block;width:100%;border-bottom-style:dashed;}.css-1h42f0z .katex .sqrt>.root{margin-left:0.27777778em;margin-right:-0.55555556em;}.css-1h42f0z .katex .sizing.reset-size1.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size1{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size1.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size2{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size1.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size3{font-size:1.4em;}.css-1h42f0z .katex .sizing.reset-size1.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size4{font-size:1.6em;}.css-1h42f0z .katex .sizing.reset-size1.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size5{font-size:1.8em;}.css-1h42f0z .katex .sizing.reset-size1.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size6{font-size:2em;}.css-1h42f0z .katex .sizing.reset-size1.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size7{font-size:2.4em;}.css-1h42f0z .katex .sizing.reset-size1.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size8{font-size:2.88em;}.css-1h42f0z .katex .sizing.reset-size1.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size9{font-size:3.456em;}.css-1h42f0z .katex .sizing.reset-size1.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size10{font-size:4.148em;}.css-1h42f0z .katex .sizing.reset-size1.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size11{font-size:4.976em;}.css-1h42f0z .katex .sizing.reset-size2.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size1{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size2.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size2{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size2.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size3{font-size:1.16666667em;}.css-1h42f0z .katex .sizing.reset-size2.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size4{font-size:1.33333333em;}.css-1h42f0z .katex .sizing.reset-size2.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size5{font-size:1.5em;}.css-1h42f0z .katex .sizing.reset-size2.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size6{font-size:1.66666667em;}.css-1h42f0z .katex .sizing.reset-size2.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size7{font-size:2em;}.css-1h42f0z .katex .sizing.reset-size2.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size8{font-size:2.4em;}.css-1h42f0z .katex .sizing.reset-size2.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size9{font-size:2.88em;}.css-1h42f0z .katex .sizing.reset-size2.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size10{font-size:3.45666667em;}.css-1h42f0z .katex .sizing.reset-size2.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size11{font-size:4.14666667em;}.css-1h42f0z .katex .sizing.reset-size3.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size1{font-size:0.71428571em;}.css-1h42f0z .katex .sizing.reset-size3.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size2{font-size:0.85714286em;}.css-1h42f0z .katex .sizing.reset-size3.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size3{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size3.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size4{font-size:1.14285714em;}.css-1h42f0z .katex .sizing.reset-size3.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size5{font-size:1.28571429em;}.css-1h42f0z .katex .sizing.reset-size3.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size6{font-size:1.42857143em;}.css-1h42f0z .katex .sizing.reset-size3.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size7{font-size:1.71428571em;}.css-1h42f0z .katex .sizing.reset-size3.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size8{font-size:2.05714286em;}.css-1h42f0z .katex .sizing.reset-size3.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size9{font-size:2.46857143em;}.css-1h42f0z .katex .sizing.reset-size3.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size10{font-size:2.96285714em;}.css-1h42f0z .katex .sizing.reset-size3.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size11{font-size:3.55428571em;}.css-1h42f0z .katex .sizing.reset-size4.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size1{font-size:0.625em;}.css-1h42f0z .katex .sizing.reset-size4.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size2{font-size:0.75em;}.css-1h42f0z .katex .sizing.reset-size4.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size3{font-size:0.875em;}.css-1h42f0z .katex .sizing.reset-size4.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size4{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size4.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size5{font-size:1.125em;}.css-1h42f0z .katex .sizing.reset-size4.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size6{font-size:1.25em;}.css-1h42f0z .katex .sizing.reset-size4.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size7{font-size:1.5em;}.css-1h42f0z .katex .sizing.reset-size4.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size8{font-size:1.8em;}.css-1h42f0z .katex .sizing.reset-size4.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size9{font-size:2.16em;}.css-1h42f0z .katex .sizing.reset-size4.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size10{font-size:2.5925em;}.css-1h42f0z .katex .sizing.reset-size4.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size11{font-size:3.11em;}.css-1h42f0z .katex .sizing.reset-size5.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size1{font-size:0.55555556em;}.css-1h42f0z .katex .sizing.reset-size5.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size2{font-size:0.66666667em;}.css-1h42f0z .katex .sizing.reset-size5.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size3{font-size:0.77777778em;}.css-1h42f0z .katex .sizing.reset-size5.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size4{font-size:0.88888889em;}.css-1h42f0z .katex .sizing.reset-size5.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size5{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size5.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size6{font-size:1.11111111em;}.css-1h42f0z .katex .sizing.reset-size5.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size7{font-size:1.33333333em;}.css-1h42f0z .katex .sizing.reset-size5.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size8{font-size:1.6em;}.css-1h42f0z .katex .sizing.reset-size5.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size9{font-size:1.92em;}.css-1h42f0z .katex .sizing.reset-size5.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size10{font-size:2.30444444em;}.css-1h42f0z .katex .sizing.reset-size5.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size11{font-size:2.76444444em;}.css-1h42f0z .katex .sizing.reset-size6.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size1{font-size:0.5em;}.css-1h42f0z .katex .sizing.reset-size6.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size2{font-size:0.6em;}.css-1h42f0z .katex .sizing.reset-size6.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size3{font-size:0.7em;}.css-1h42f0z .katex .sizing.reset-size6.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size4{font-size:0.8em;}.css-1h42f0z .katex .sizing.reset-size6.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size5{font-size:0.9em;}.css-1h42f0z .katex .sizing.reset-size6.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size6{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size6.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size7{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size6.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size8{font-size:1.44em;}.css-1h42f0z .katex .sizing.reset-size6.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size9{font-size:1.728em;}.css-1h42f0z .katex .sizing.reset-size6.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size10{font-size:2.074em;}.css-1h42f0z .katex .sizing.reset-size6.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size11{font-size:2.488em;}.css-1h42f0z .katex .sizing.reset-size7.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size1{font-size:0.41666667em;}.css-1h42f0z .katex .sizing.reset-size7.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size2{font-size:0.5em;}.css-1h42f0z .katex .sizing.reset-size7.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size3{font-size:0.58333333em;}.css-1h42f0z .katex .sizing.reset-size7.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size4{font-size:0.66666667em;}.css-1h42f0z .katex .sizing.reset-size7.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size5{font-size:0.75em;}.css-1h42f0z .katex .sizing.reset-size7.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size6{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size7.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size7{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size7.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size8{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size7.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size9{font-size:1.44em;}.css-1h42f0z .katex .sizing.reset-size7.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size10{font-size:1.72833333em;}.css-1h42f0z .katex .sizing.reset-size7.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size11{font-size:2.07333333em;}.css-1h42f0z .katex .sizing.reset-size8.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size1{font-size:0.34722222em;}.css-1h42f0z .katex .sizing.reset-size8.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size2{font-size:0.41666667em;}.css-1h42f0z .katex .sizing.reset-size8.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size3{font-size:0.48611111em;}.css-1h42f0z .katex .sizing.reset-size8.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size4{font-size:0.55555556em;}.css-1h42f0z .katex .sizing.reset-size8.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size5{font-size:0.625em;}.css-1h42f0z .katex .sizing.reset-size8.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size6{font-size:0.69444444em;}.css-1h42f0z .katex .sizing.reset-size8.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size7{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size8.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size8{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size8.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size9{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size8.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size10{font-size:1.44027778em;}.css-1h42f0z .katex .sizing.reset-size8.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size11{font-size:1.72777778em;}.css-1h42f0z .katex .sizing.reset-size9.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size1{font-size:0.28935185em;}.css-1h42f0z .katex .sizing.reset-size9.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size2{font-size:0.34722222em;}.css-1h42f0z .katex .sizing.reset-size9.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size3{font-size:0.40509259em;}.css-1h42f0z .katex .sizing.reset-size9.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size4{font-size:0.46296296em;}.css-1h42f0z .katex .sizing.reset-size9.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size5{font-size:0.52083333em;}.css-1h42f0z .katex .sizing.reset-size9.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size6{font-size:0.5787037em;}.css-1h42f0z .katex .sizing.reset-size9.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size7{font-size:0.69444444em;}.css-1h42f0z .katex .sizing.reset-size9.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size8{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size9.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size9{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size9.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size10{font-size:1.20023148em;}.css-1h42f0z .katex .sizing.reset-size9.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size11{font-size:1.43981481em;}.css-1h42f0z .katex .sizing.reset-size10.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size1{font-size:0.24108004em;}.css-1h42f0z .katex .sizing.reset-size10.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size2{font-size:0.28929605em;}.css-1h42f0z .katex .sizing.reset-size10.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size3{font-size:0.33751205em;}.css-1h42f0z .katex .sizing.reset-size10.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size4{font-size:0.38572806em;}.css-1h42f0z .katex .sizing.reset-size10.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size5{font-size:0.43394407em;}.css-1h42f0z .katex .sizing.reset-size10.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size6{font-size:0.48216008em;}.css-1h42f0z .katex .sizing.reset-size10.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size7{font-size:0.57859209em;}.css-1h42f0z .katex .sizing.reset-size10.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size8{font-size:0.69431051em;}.css-1h42f0z .katex .sizing.reset-size10.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size9{font-size:0.83317261em;}.css-1h42f0z .katex .sizing.reset-size10.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size10{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size10.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size11{font-size:1.19961427em;}.css-1h42f0z .katex .sizing.reset-size11.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size1{font-size:0.20096463em;}.css-1h42f0z .katex .sizing.reset-size11.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size2{font-size:0.24115756em;}.css-1h42f0z .katex .sizing.reset-size11.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size3{font-size:0.28135048em;}.css-1h42f0z .katex .sizing.reset-size11.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size4{font-size:0.32154341em;}.css-1h42f0z .katex .sizing.reset-size11.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size5{font-size:0.36173633em;}.css-1h42f0z .katex .sizing.reset-size11.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size6{font-size:0.40192926em;}.css-1h42f0z .katex .sizing.reset-size11.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size7{font-size:0.48231511em;}.css-1h42f0z .katex .sizing.reset-size11.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size8{font-size:0.57877814em;}.css-1h42f0z .katex .sizing.reset-size11.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size9{font-size:0.69453376em;}.css-1h42f0z .katex .sizing.reset-size11.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size10{font-size:0.83360129em;}.css-1h42f0z .katex .sizing.reset-size11.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size11{font-size:1em;}.css-1h42f0z .katex .delimsizing.size1{font-family:KaTeX_Size1;}.css-1h42f0z .katex .delimsizing.size2{font-family:KaTeX_Size2;}.css-1h42f0z .katex .delimsizing.size3{font-family:KaTeX_Size3;}.css-1h42f0z .katex .delimsizing.size4{font-family:KaTeX_Size4;}.css-1h42f0z .katex .delimsizing.mult .delim-size1>span{font-family:KaTeX_Size1;}.css-1h42f0z .katex .delimsizing.mult .delim-size4>span{font-family:KaTeX_Size4;}.css-1h42f0z .katex .nulldelimiter{display:inline-block;width:0.12em;}.css-1h42f0z .katex .delimcenter{position:relative;}.css-1h42f0z .katex .op-symbol{position:relative;}.css-1h42f0z .katex .op-symbol.small-op{font-family:KaTeX_Size1;}.css-1h42f0z .katex .op-symbol.large-op{font-family:KaTeX_Size2;}.css-1h42f0z .katex .op-limits>.vlist-t{text-align:center;}.css-1h42f0z .katex .accent>.vlist-t{text-align:center;}.css-1h42f0z .katex .accent .accent-body{position:relative;}.css-1h42f0z .katex .accent .accent-body:not(.accent-full){width:0;}.css-1h42f0z .katex .overlay{display:block;}.css-1h42f0z .katex .mtable .vertical-separator{display:inline-block;min-width:1px;}.css-1h42f0z .katex .mtable .arraycolsep{display:inline-block;}.css-1h42f0z .katex .mtable .col-align-c>.vlist-t{text-align:center;}.css-1h42f0z .katex .mtable .col-align-l>.vlist-t{text-align:left;}.css-1h42f0z .katex .mtable .col-align-r>.vlist-t{text-align:right;}.css-1h42f0z .katex .svg-align{text-align:left;}.css-1h42f0z .katex svg{display:block;position:absolute;width:100%;height:inherit;fill:currentColor;stroke:currentColor;fill-rule:nonzero;fill-opacity:1;stroke-width:1;stroke-linecap:butt;stroke-linejoin:miter;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1;}.css-1h42f0z .katex svg path{stroke:none;}.css-1h42f0z .katex img{border-style:none;min-width:0;min-height:0;max-width:none;max-height:none;}.css-1h42f0z .katex .stretchy{width:100%;display:block;position:relative;overflow:hidden;}.css-1h42f0z .katex .stretchy::before,.css-1h42f0z .katex .stretchy::after{content:'';}.css-1h42f0z .katex .hide-tail{width:100%;position:relative;overflow:hidden;}.css-1h42f0z .katex .halfarrow-left{position:absolute;left:0;width:50.2%;overflow:hidden;}.css-1h42f0z .katex .halfarrow-right{position:absolute;right:0;width:50.2%;overflow:hidden;}.css-1h42f0z .katex .brace-left{position:absolute;left:0;width:25.1%;overflow:hidden;}.css-1h42f0z .katex .brace-center{position:absolute;left:25%;width:50%;overflow:hidden;}.css-1h42f0z .katex .brace-right{position:absolute;right:0;width:25.1%;overflow:hidden;}.css-1h42f0z .katex .x-arrow-pad{padding:0 0.5em;}.css-1h42f0z .katex .cd-arrow-pad{padding:0 0.55556em 0 0.27778em;}.css-1h42f0z .katex .x-arrow,.css-1h42f0z .katex .mover,.css-1h42f0z .katex .munder{text-align:center;}.css-1h42f0z .katex .boxpad{padding:0 0.3em 0 0.3em;}.css-1h42f0z .katex .fbox,.css-1h42f0z .katex .fcolorbox{box-sizing:border-box;border:0.04em solid;}.css-1h42f0z .katex .cancel-pad{padding:0 0.2em 0 0.2em;}.css-1h42f0z .katex .cancel-lap{margin-left:-0.2em;margin-right:-0.2em;}.css-1h42f0z .katex .sout{border-bottom-style:solid;border-bottom-width:0.08em;}.css-1h42f0z .katex .angl{box-sizing:border-box;border-top:0.049em solid;border-right:0.049em solid;margin-right:0.03889em;}.css-1h42f0z .katex .anglpad{padding:0 0.03889em 0 0.03889em;}.css-1h42f0z .katex .eqn-num::before{counter-increment:katexEqnNo;content:'(' counter(katexEqnNo) ')';}.css-1h42f0z .katex .mml-eqn-num::before{counter-increment:mmlEqnNo;content:'(' counter(mmlEqnNo) ')';}.css-1h42f0z .katex .mtr-glue{width:50%;}.css-1h42f0z .katex .cd-vert-arrow{display:inline-block;position:relative;}.css-1h42f0z .katex .cd-label-left{display:inline-block;position:absolute;right:calc(50% + 0.3em);text-align:left;}.css-1h42f0z .katex .cd-label-right{display:inline-block;position:absolute;left:calc(50% + 0.3em);text-align:right;}.css-1h42f0z .katex-display{display:block;margin:1em 0;text-align:center;}.css-1h42f0z .katex-display>.katex{display:block;white-space:nowrap;}.css-1h42f0z .katex-display>.katex>.katex-html{display:block;position:relative;}.css-1h42f0z .katex-display>.katex>.katex-html>.tag{position:absolute;right:0;}.css-1h42f0z .katex-display.leqno>.katex>.katex-html>.tag{left:0;right:auto;}.css-1h42f0z .katex-display.fleqn>.katex{text-align:left;padding-left:2em;}.css-1h42f0z body{counter-reset:katexEqnNo mmlEqnNo;}.css-1h42f0z .link-like{color:#007bff;-webkit-text-decoration:underline;text-decoration:underline;}.css-1h42f0z .text-overline{-webkit-text-decoration:overline;text-decoration:overline;}.css-1h42f0z code,.css-1h42f0z kbd,.css-1h42f0z pre,.css-1h42f0z samp{font-family:monospace;}.css-1h42f0z code{padding:2px 4px;color:#444;background:#ddd;border-radius:4px;}.css-1h42f0z figcaption,.css-1h42f0z caption{text-align:center;}.css-1h42f0z figcaption{font-size:12px;font-style:italic;overflow:hidden;}.css-1h42f0z h3{font-size:1.75rem;}.css-1h42f0z h4{font-size:1.5rem;}.css-1h42f0z .mathBlock{font-size:24px;-webkit-padding-start:4px;padding-inline-start:4px;}.css-1h42f0z .mathBlock .katex{font-size:24px;text-align:left;}.css-1h42f0z .math-inline{background-color:#f0f0f0;display:inline-block;font-size:inherit;padding:0 3px;}.css-1h42f0z .videoBlock,.css-1h42f0z .imageBlock{margin-bottom:16px;}.css-1h42f0z .imageBlockimage-align--left,.css-1h42f0z .videoBlockvideo-align--left{float:left;}.css-1h42f0z .imageBlockimage-align--right,.css-1h42f0z .videoBlockvideo-align--right{float:right;}.css-1h42f0z .imageBlockimage-align--center,.css-1h42f0z .videoBlockvideo-align--center{display:block;margin-left:auto;margin-right:auto;clear:both;}.css-1h42f0z .imageBlockimage-align--none,.css-1h42f0z .videoBlockvideo-align--none{clear:both;margin-left:0;margin-right:0;}.css-1h42f0z .videoBlockvideo--wrapper{position:relative;padding-bottom:56.25%;height:0;}.css-1h42f0z .videoBlockvideo--wrapper iframe{position:absolute;top:0;left:0;width:100%;height:100%;}.css-1h42f0z .videoBlockcaption{text-align:left;}.css-1h42f0z table{width:-webkit-max-content;width:-moz-max-content;width:max-content;}.css-1h42f0z .tableBlock{max-width:100%;margin-bottom:1rem;overflow-y:scroll;}.css-1h42f0z .tableBlock thead,.css-1h42f0z .tableBlock thead th{border-bottom:1px solid #333!important;}.css-1h42f0z .tableBlock th,.css-1h42f0z .tableBlock td{padding:10px;text-align:left;}.css-1h42f0z .tableBlock th{font-weight:bold!important;}.css-1h42f0z .tableBlock caption{caption-side:bottom;color:#555;font-size:12px;font-style:italic;text-align:center;}.css-1h42f0z .tableBlock caption>p{margin:0;}.css-1h42f0z .tableBlock th>p,.css-1h42f0z .tableBlock td>p{margin:0;}.css-1h42f0z .tableBlock [data-background-color='aliceblue']{background-color:#f0f8ff;color:#000;}.css-1h42f0z .tableBlock [data-background-color='black']{background-color:#000;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='chocolate']{background-color:#d2691e;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='cornflowerblue']{background-color:#6495ed;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='crimson']{background-color:#dc143c;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='darkblue']{background-color:#00008b;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='darkseagreen']{background-color:#8fbc8f;color:#000;}.css-1h42f0z .tableBlock [data-background-color='deepskyblue']{background-color:#00bfff;color:#000;}.css-1h42f0z .tableBlock [data-background-color='gainsboro']{background-color:#dcdcdc;color:#000;}.css-1h42f0z .tableBlock [data-background-color='grey']{background-color:#808080;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='lemonchiffon']{background-color:#fffacd;color:#000;}.css-1h42f0z .tableBlock [data-background-color='lightpink']{background-color:#ffb6c1;color:#000;}.css-1h42f0z .tableBlock [data-background-color='lightsalmon']{background-color:#ffa07a;color:#000;}.css-1h42f0z .tableBlock [data-background-color='lightskyblue']{background-color:#87cefa;color:#000;}.css-1h42f0z .tableBlock [data-background-color='mediumblue']{background-color:#0000cd;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='omnigrey']{background-color:#f0f0f0;color:#000;}.css-1h42f0z .tableBlock [data-background-color='white']{background-color:#fff;color:#000;}.css-1h42f0z .tableBlock [data-text-align='center']{text-align:center;}.css-1h42f0z .tableBlock [data-text-align='left']{text-align:left;}.css-1h42f0z .tableBlock [data-text-align='right']{text-align:right;}.css-1h42f0z .tableBlock [data-vertical-align='bottom']{vertical-align:bottom;}.css-1h42f0z .tableBlock [data-vertical-align='middle']{vertical-align:middle;}.css-1h42f0z .tableBlock [data-vertical-align='top']{vertical-align:top;}.css-1h42f0z .tableBlockfont-size--xxsmall{font-size:10px;}.css-1h42f0z .tableBlockfont-size--xsmall{font-size:12px;}.css-1h42f0z .tableBlockfont-size--small{font-size:14px;}.css-1h42f0z .tableBlockfont-size--large{font-size:18px;}.css-1h42f0z .tableBlockborder--some tbody tr:not(:last-child){border-bottom:1px solid #e2e5e7;}.css-1h42f0z .tableBlockborder--bordered td,.css-1h42f0z .tableBlockborder--bordered th{border:1px solid #e2e5e7;}.css-1h42f0z .tableBlockborder--borderless tbody+tbody,.css-1h42f0z .tableBlockborder--borderless td,.css-1h42f0z .tableBlockborder--borderless th,.css-1h42f0z .tableBlockborder--borderless tr,.css-1h42f0z .tableBlockborder--borderless thead,.css-1h42f0z .tableBlockborder--borderless thead th{border:0!important;}.css-1h42f0z .tableBlock:not(.tableBlocktable-striped) tbody tr{background-color:unset!important;}.css-1h42f0z .tableBlocktable-striped tbody tr:nth-of-type(odd){background-color:#f9fafc!important;}.css-1h42f0z .tableBlocktable-compactl th,.css-1h42f0z .tableBlocktable-compact td{padding:3px!important;}.css-1h42f0z .tableBlockfull-size{width:100%;}.css-1h42f0z .textBlock{margin-bottom:16px;}.css-1h42f0z .textBlocktext-formatting--finePrint{font-size:12px;}.css-1h42f0z .textBlocktext-infoBox{padding:0.75rem 1.25rem;margin-bottom:1rem;border:1px solid transparent;border-radius:0.25rem;}.css-1h42f0z .textBlocktext-infoBox p{margin:0;}.css-1h42f0z .textBlocktext-infoBox--primary{background-color:#cce5ff;border-color:#b8daff;color:#004085;}.css-1h42f0z .textBlocktext-infoBox--secondary{background-color:#e2e3e5;border-color:#d6d8db;color:#383d41;}.css-1h42f0z .textBlocktext-infoBox--success{background-color:#d4edda;border-color:#c3e6cb;color:#155724;}.css-1h42f0z .textBlocktext-infoBox--danger{background-color:#f8d7da;border-color:#f5c6cb;color:#721c24;}.css-1h42f0z .textBlocktext-infoBox--warning{background-color:#fff3cd;border-color:#ffeeba;color:#856404;}.css-1h42f0z .textBlocktext-infoBox--info{background-color:#d1ecf1;border-color:#bee5eb;color:#0c5460;}.css-1h42f0z .textBlock__text-infoBox--dark{background-color:#d6d8d9;border-color:#c6c8ca;color:#1b1e21;}.css-1h42f0z.css-1h42f0z{color:#2B3148;background-color:transparent;font-family:var(--calculator-ui-font-family),Verdana,sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-1h42f0z.css-1h42f0z:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-1h42f0z .js-external-link-button.link-like,.css-1h42f0z .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-1h42f0z .js-external-link-button.link-like:hover,.css-1h42f0z .js-external-link-anchor:hover,.css-1h42f0z .js-external-link-button.link-like:active,.css-1h42f0z .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-1h42f0z .js-external-link-button.link-like:focus-visible,.css-1h42f0z .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-1h42f0z p,.css-1h42f0z div{margin:0;display:block;}.css-1h42f0z pre{margin:0;display:block;}.css-1h42f0z pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-1h42f0z pre:not(:first-child){padding-top:8px;}.css-1h42f0z ul,.css-1h42f0z ol{display:block margin:0;padding-left:20px;}.css-1h42f0z ul li,.css-1h42f0z ol li{padding-top:8px;}.css-1h42f0z ul ul,.css-1h42f0z ol ul,.css-1h42f0z ul ol,.css-1h42f0z ol ol{padding-top:0;}.css-1h42f0z ul:not(:first-child),.css-1h42f0z ol:not(:first-child){padding-top:4px;} Test setup

Choose test type

t-test for the population mean, μ, based on one independent sample . Null hypothesis H 0 : μ = μ 0

Alternative hypothesis H 1

Test details

Significance level α

The probability that we reject a true H 0 (type I error).

Degrees of freedom

Calculated as sample size minus one.

Test results

Statistics with Python
Data Analysis Tutorial
Python â€“ Data visualization tutorial
Machine Learning Projects
Machine Learning Interview Questions
Machine Learning Mathematics
Deep Learning Tutorial
Deep Learning Project
Deep Learning Interview Questions
Computer Vision Tutorial
Computer Vision Projects
NLP Project
NLP Interview Questions
100 Days of Machine Learning

Difference Between One-Tailed and Two-Tailed Tests

One and Two-Tailed Tests are ways to identify the relationship between the statistical variables. For checking the relationship between variables in a single direction (Left or Right direction), we use a one-tailed test. A two-tailed test is used to check whether the relations between variables are in any direction or not.

One-Tailed Test

A one-tailed test is based on a uni-directional hypothesis where the area of rejection is on only one side of the sampling distribution. It determines whether a particular population parameter is larger or smaller than the predefined parameter. It uses one single critical value to test the data.

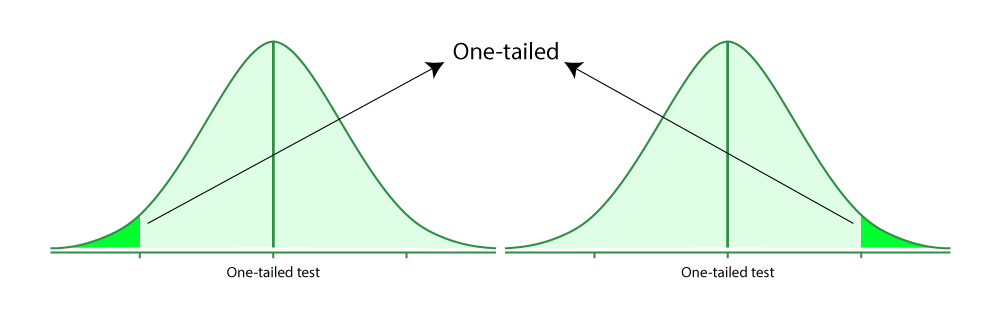
Alternative Hypothesis ( H 1):

$H_1: \theta > \theta_0$

Test Statistic: Depending on the type of test and the distribution, the test statistic is computed ( Z -score for normal distribution).

Decision Rule: If the test statistic falls in the critical region, reject the null hypothesis in favor of the alternative hypothesis.

Example: Effect of participants of students in coding competition on their fear level.

H0: There is no important effect of students in coding competition on their fear level.

The main intention is to check the decreased fear level when students participate in a coding competition.

Two-Tailed Test

A two-tailed test is also called a nondirectional hypothesis. For checking whether the sample is greater or less than a range of values, we use the two-tailed. It is used for null hypothesis testing.

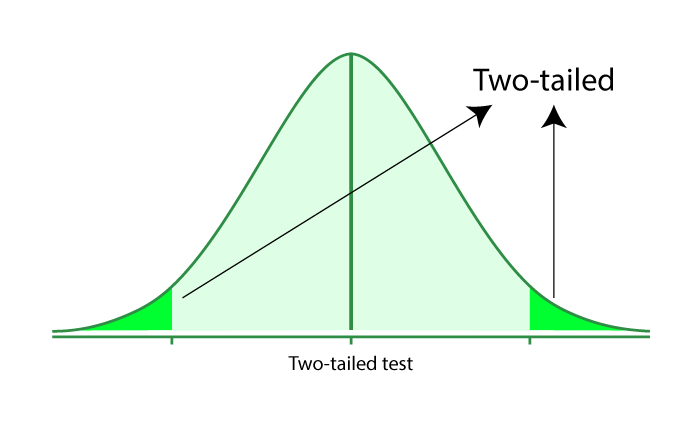
Test Statistic: Compute the test statistic as appropriate for the distribution ( Z -score for normal distribution).

Decision Rule: If the test statistic falls in either tail of the distribution’s critical region, reject the null hypothesis in favor of the alternative hypothesis.

Example: Effect of new bill pass on the loan of farmers.

H0: There is no significant effect of the new bill passed on loans of farmers.

New bill passes can affect in both ways either increase or decrease the loan of farmers.

Difference Between One and Two-Tailed Test:

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Statistics Tutorial

Descriptive statistics, inferential statistics, stat reference, statistics - hypothesis testing a mean (two tailed).

A population mean is an average of value a population.

Hypothesis tests are used to check a claim about the size of that population mean.

Hypothesis Testing a Mean

The following steps are used for a hypothesis test:

Check the conditions
Define the claims
Decide the significance level
Calculate the test statistic

For example:

Population : Nobel Prize winners
Category : Age when they received the prize.

And we want to check the claim:

"The average age of Nobel Prize winners when they received the prize is not 60"

By taking a sample of 30 randomly selected Nobel Prize winners we could find that:

The mean age in the sample ($\bar{x}$) is 62.1
The standard deviation of age in the sample ($s$) is 13.46

From this sample data we check the claim with the steps below.

1. Checking the Conditions

The conditions for calculating a confidence interval for a proportion are:

The sample is randomly selected
The population data is normally distributed
Sample size is large enough

A moderately large sample size, like 30, is typically large enough.

In the example, the sample size was 30 and it was randomly selected, so the conditions are fulfilled.

Note: Checking if the data is normally distributed can be done with specialized statistical tests.

2. Defining the Claims

We need to define a null hypothesis ($H_{0}$) and an alternative hypothesis ($H_{1}$) based on the claim we are checking.

The claim was:

In this case, the parameter is the mean age of Nobel Prize winners when they received the prize ($\mu$).

The null and alternative hypothesis are then:

Null hypothesis : The average age was 60.

Alternative hypothesis : The average age is not 60.

Which can be expressed with symbols as:

$H_{0}$: $\mu = 60 $

$H_{1}$: $\mu \neq 60 $

This is a ' two-tailed ' test, because the alternative hypothesis claims that the proportion is different from the null hypothesis.

If the data supports the alternative hypothesis, we reject the null hypothesis and accept the alternative hypothesis.

3. Deciding the Significance Level

The significance level ($\alpha$) is the uncertainty we accept when rejecting the null hypothesis in a hypothesis test.

The significance level is a percentage probability of accidentally making the wrong conclusion.

Typical significance levels are:

$\alpha = 0.1$ (10%)
$\alpha = 0.05$ (5%)
$\alpha = 0.01$ (1%)

A lower significance level means that the evidence in the data needs to be stronger to reject the null hypothesis.

There is no "correct" significance level - it only states the uncertainty of the conclusion.

Note: A 5% significance level means that when we reject a null hypothesis:

We expect to reject a true null hypothesis 5 out of 100 times.

4. Calculating the Test Statistic

The test statistic is used to decide the outcome of the hypothesis test.

The test statistic is a standardized value calculated from the sample.

The formula for the test statistic (TS) of a population mean is:

$\displaystyle \frac{\bar{x} - \mu}{s} \cdot \sqrt{n} $

$\bar{x}-\mu$ is the difference between the sample mean ($\bar{x}$) and the claimed population mean ($\mu$).

$s$ is the sample standard deviation .

$n$ is the sample size.

In our example:

The claimed ($H_{0}$) population mean ($\mu$) was $ 60 $

The sample mean ($\bar{x}$) was $62.1$

The sample standard deviation ($s$) was $13.46$

The sample size ($n$) was $30$

So the test statistic (TS) is then:

$\displaystyle \frac{62.1-60}{13.46} \cdot \sqrt{30} = \frac{2.1}{13.46} \cdot \sqrt{30} \approx 0.156 \cdot 5.477 = \underline{0.855}$

You can also calculate the test statistic using programming language functions:

With Python use the scipy and math libraries to calculate the test statistic.

With R use built-in math and statistics functions to calculate the test statistic.

5. Concluding

There are two main approaches for making the conclusion of a hypothesis test:

The critical value approach compares the test statistic with the critical value of the significance level.
The P-value approach compares the P-value of the test statistic and with the significance level.

Note: The two approaches are only different in how they present the conclusion.

The Critical Value Approach

For the critical value approach we need to find the critical value (CV) of the significance level ($\alpha$).

For a population mean test, the critical value (CV) is a T-value from a student's t-distribution .

This critical T-value (CV) defines the rejection region for the test.

The rejection region is an area of probability in the tails of the standard normal distribution.

Because the claim is that the population proportion is different from 60, the rejection region is split into both the left and right tail:

The student's t-distribution is adjusted for the uncertainty from smaller samples.

This adjustment is called degrees of freedom (df), which is the sample size $(n) - 1$

In this case the degrees of freedom (df) is: $30 - 1 = \underline{29} $

Choosing a significance level ($\alpha$) of 0.05, or 5%, we can find the critical T-value from a T-table , or with a programming language function:

Note: Because this is a two-tailed test the tail area ($\alpha$) needs to be split in half (divided by 2).

With Python use the Scipy Stats library t.ppf() function find the T-Value for an $\alpha$/2 = 0.025 at 29 degrees of freedom (df).

With R use the built-in qt() function to find the t-value for an $\alpha$/ = 0.025 at 29 degrees of freedom (df).

Using either method we can find that the critical T-Value is $\approx \underline{-2.045}$

For a two-tailed test we need to check if the test statistic (TS) is smaller than the negative critical value (-CV), or bigger than the positive critical value (CV).

If the test statistic is smaller than the negative critical value, the test statistic is in the rejection region .

If the test statistic is bigger than the positive critical value, the test statistic is in the rejection region .

When the test statistic is in the rejection region, we reject the null hypothesis ($H_{0}$).

Here, the test statistic (TS) was $\approx \underline{0.855}$ and the critical value was $\approx \underline{-2.045}$

Here is an illustration of this test in a graph:

Since the test statistic is between the critical values we keep the null hypothesis.

This means that the sample data does not support the alternative hypothesis.

And we can summarize the conclusion stating:

The sample data does not support the claim that "The average age of Nobel Prize winners when they received the prize is not 60" at a 5% significance level .

The P-Value Approach

For the P-value approach we need to find the P-value of the test statistic (TS).

If the P-value is smaller than the significance level ($\alpha$), we reject the null hypothesis ($H_{0}$).

The test statistic was found to be $ \approx \underline{0.855} $

For a population proportion test, the test statistic is a T-Value from a student's t-distribution .

Because this is a two-tailed test, we need to find the P-value of a T-value bigger than 0.855 and multiply it by 2 .

The student's t-distribution is adjusted according to degrees of freedom (df), which is the sample size $(30) - 1 = \underline{29}$

We can find the P-value using a T-table , or with a programming language function:

With Python use the Scipy Stats library t.cdf() function find the P-value of a T-value bigger than 0.855 for a two tailed test at 29 degrees of freedom (df):

With R use the built-in pt() function find the P-value of a T-Value bigger than 0.855 for a two tailed test at 29 degrees of freedom (df):

Using either method we can find that the P-value is $\approx \underline{0.3996}$

This tells us that the significance level ($\alpha$) would need to be smaller 0.3996, or 39.96%, to reject the null hypothesis.

This P-value is bigger than any of the common significance levels (10%, 5%, 1%).

So the null hypothesis is kept at all of these significance levels.

The sample data does not support the claim that "The average age of Nobel Prize winners when they received the prize is not 60" at a 10%, 5%, or 1% significance level .

Calculating a P-Value for a Hypothesis Test with Programming

Many programming languages can calculate the P-value to decide outcome of a hypothesis test.

Using software and programming to calculate statistics is more common for bigger sets of data, as calculating manually becomes difficult.

The P-value calculated here will tell us the lowest possible significance level where the null-hypothesis can be rejected.

With Python use the scipy and math libraries to calculate the P-value for a two tailed hypothesis test for a mean.

Here, the sample size is 30, the sample mean is 62.1, the sample standard deviation is 13.46, and the test is for a mean different from 60.

With R use built-in math and statistics functions find the P-value for a two tailed hypothesis test for a mean.

Left-Tailed and Two-Tailed Tests

This was an example of a left tailed test, where the alternative hypothesis claimed that parameter is smaller than the null hypothesis claim.

You can check out an equivalent step-by-step guide for other types here:

Right-Tailed Test
Two-Tailed Test

COLOR PICKER

Contact Sales

If you want to use W3Schools services as an educational institution, team or enterprise, send us an e-mail: [email protected]

Report Error

If you want to report an error, or if you want to make a suggestion, send us an e-mail: [email protected]

One-Tailed vs Two-Tailed Tests; What You Should Know

Understanding the different methods of hypothesis testing is crucial for accurate data interpretation. Among these methods, one-tailed and two-tailed tests stand out due to their specific applications and implications.

This article discusses one-tailed vs two-tailed tests, their examples, scenarios where each test is applicable, and the pros and cons associated with one-tailed and two-tailed tests.

What is a One-Tailed Test?

One-tailed tests are used when a hypothesis predicts a specific direction of effect. They are ideal for scenarios where the interest lies in determining whether a parameter is significantly greater or less than a specific value.

This type of test evaluates whether the observed data deviates significantly from the null hypothesis (the hypothesis of no effect or no difference) but only in the specified direction.

In the context of A/B testing , a one-tailed test is used to determine if there is a significant difference in a specific direction between two webpage versions, products, or strategies.

For example, if you conduct an A/B test to see if a new website design leads to higher user engagement compared to the current design, a one-tailed test would be used to assess if the new design increases engagement specifically, ignoring the possibility of a decrease.

This focused approach makes one-tailed tests suitable for scenarios where you expect a directional and clearly defined outcome.

Example of a One-Tailed Test in A/B Testing:

Suppose an e-commerce company wants to increase its website’s conversion rate . The CRO team they hired hypothesizes that changing the color of the “Add to Cart” button from blue to red will lead to more clicks and, consequently, more purchases. To test this hypothesis, they set up an A/B test:

Version A (Control): The original webpage with the blue “Add to Cart” button.

Version B (Variant): The same webpage but with the red “Add to Cart” button.

The hypothesis predicts the red button will increase conversions. The null hypothesis (H0) states there will be no increase, or possibly a decrease, in conversions with the red button.

A one-tailed test checks for increased conversions with the red button. If the test shows statistical significance, it supports the hypothesis that the red button performs better. If not, there’s insufficient evidence to reject the null hypothesis, meaning the increase isn’t statistically significant.

Pros of one-tailed tests

Increased power.

One-tailed tests have more statistical power compared to two-tailed tests when testing the same hypothesis. They focus all statistical power in one direction of the distribution (the direction of interest), making it more likely to detect an effect in that direction.

Lower Sample Size Requirement

Due to its increased power, a one-tailed test often requires a smaller sample size to achieve the same level of statistical significance as a two-tailed test. This is a significant advantage in practical scenarios where collecting large samples can be time-consuming or expensive.

Specific Hypothesis Testing

One-tailed tests are tailored for specific, directional hypotheses. This means they are ideal when the hypothesis makes a specific prediction about the direction of the effect. For example, if a hypothesis states that a new marketing strategy will increase sales, a one-tailed test is appropriate because it specifically looks for an increase in sales.

Cons of one-tailed tests

Risk of missing opposite effect.

One of the main drawbacks of a one-tailed test is the risk of missing a significant effect in the opposite direction of the hypothesis. Since the test is designed to detect an effect in one specific direction, it may overlook meaningful changes that occur in the other direction.

Choosing a one-tailed test, especially after data collection, poses a risk of bias. Decisions should be based on strong theoretical grounds or prior evidence, not on a desire to achieve significant results.

Limited Insight

One-tailed tests provide less comprehensive insight compared to two-tailed tests. By focusing only on one direction, they may miss out on understanding the full spectrum of the effect being studied.

What is a Two-Tailed Test?

A two-tailed test is a statistical method used when the direction of the effect is not specified in the hypothesis; unlike a one-tailed test that looks for a significant effect in one specific direction, a two-tailed test checks for significance in both directions.

This type of test is useful when you are interested in detecting any significant difference, regardless of whether it is positive or negative.

A/B testing uses a two-tailed test to determine whether a statistically significant difference exists between two versions (A and B) without a predetermined direction of the expected outcome.

This approach is crucial when the goal is to ascertain any significant change, whether an increase or a decrease, in a key metric due to variations in the test.

For instance, a two-tailed test is appropriate if you test two different website layouts to see which one performs better in terms of user engagement without a specific hypothesis about which layout will be superior.

Example of a Two-Tailed Test in A/B Testing:

The same ecommerce company wants to evaluate the impact of a new product description format on its website. The company is unsure whether the new format will increase or decrease customer engagement, so they conducted an A/B test again.

Version A (Control) : The original product page with the standard description format.

Version B (Variant): The same product page but with the new description format.

The hypothesis is: “The new format will significantly impact engagement,” without specifying the direction of this impact.

A two-tailed test is chosen to detect any significant change in engagement, whether an increase or decrease. It assesses if the new format leads to a statistically significant difference in engagement compared to the control.

If the test shows significance, it confirms the new format notably affects engagement, but further analysis is required to determine if the effect is positive or negative.

Pros of two-tailed tests

Detects effects in both directions.

The primary advantage of a two-tailed test is its ability to detect statistically significant effects in both directions. This means it can identify whether the tested variable has a positive or negative impact compared to the control.

More Conservative

A two-tailed test is considered more conservative than a one-tailed test because it divides the significance level across both ends of the distribution. This means that for a result to be considered statistically significant, it must meet a stricter criterion compared to a one-tailed test.

Cons of two-tailed tests

Reduced power.

One of the main drawbacks of a two-tailed test is its reduced statistical power compared to a one-tailed test. The power of a statistical test is its ability to detect an effect when there is one. In a two-tailed test, because the significance level is split between both tails of the distribution, it requires a stronger effect to reach statistical significance .

Larger Sample Size Needed

Due to its reduced power, a two-tailed test often requires a larger sample size to achieve the same level of statistical significance as a one-tailed test. This can be a significant challenge in research scenarios where gathering a large amount of data is difficult, time-consuming, or expensive.

Overly General

In A/B testing, a two-tailed test can be overly general when there’s already a strong theory predicting the direction of an effect. It checks for changes in both directions, which may not be necessary if you only expect an increase or decrease.

One-Tailed vs Two-Tailed Tests: Which Should You Choose?

When deciding between a one-tailed and a two-tailed test in A/B testing, the choice hinges on your hypothesis and what you aim to discover or prove. Both tests have their place, but their applicability depends on the specific context of your research question.

Understanding the differences between these tests, their applications, and their implications is vital for accurate data interpretation and effective decision-making in various testing scenarios.

Product-Market Fit; What it is, and How to Achieve It?

11 Google Analytics Alternatives You Should Know

Session Recordings
Knowledge Base

Type above and press Enter to search. Press Esc to cancel.

COMMENTS

Two-Tailed Hypothesis Tests: 3 Example Problems
Learn how to perform two-tailed hypothesis tests with three real-world examples involving widgets, plants, and exam scores. A two-tailed test is used when the alternative hypothesis contains the not equal (≠) sign, indicating that any effect is possible.
One-Tailed and Two-Tailed Hypothesis Tests Explained
Learn the differences, advantages and disadvantages of one-tailed and two-tailed hypothesis tests. A one-tailed test can only detect an effect in one direction, while a two-tailed test can detect effects in both directions.
What Is a Two-Tailed Test? Definition and Example
A two-tailed test is a statistical method that tests whether a sample mean is significantly different from a population mean in both directions. Learn how to conduct a two-tailed test, see an ...
One- and two-tailed tests
Learn the difference between one-tailed and two-tailed tests in statistical significance testing, with examples and applications. A one-tailed test is appropriate if the estimated value may depart from the reference value in only one direction, while a two-tailed test is appropriate if the estimated value may depart in either direction.
Two Sample t-test: Definition, Formula, and Example
Learn how to perform a two sample t-test to compare the means of two populations using a simple formula and a step-by-step example. Find out the assumptions, hypotheses, and p-value of this statistical test.
t-test Calculator
Learn how to perform one-sample, two-sample, and paired t-tests with this online calculator. Find out the p-value, critical values, and degrees of freedom for each test, and when to use a two-tailed or one-tailed test.
Difference Between One-Tailed and Two-Tailed Tests
Learn the difference between one-tailed and two-tailed tests, which are ways to identify the relationship between statistical variables. See the null and alternative hypotheses, test statistics, decision rules, and examples for each type of test.
Two Tailed Test: Definition, Examples
But with a two tailed test, that 5% is split between the two tails, giving you 2.5% (0.025) in each tail. Need help with a homework question? Check out our tutoring page! Two Tailed T Test Image: ETSU.edu. You may want to compare a sample mean to a given value of x with a t test. Let's say your null hypothesis is that the mean is equal to 10 ...
Statistics
# Output the p-value of the test statistic (two tailed test) print(2*(1-stats.t.cdf(test_stat, n-1))) Try it Yourself » Example. With R use built-in math and statistics functions find the P-value for a two tailed hypothesis test for a mean. Here, the sample size is 30, the sample mean is 62.1, the sample standard deviation is 13.46, and the ...
One-Tailed vs Two-Tailed Tests; What You Should Know
Learn the difference between one-tailed and two-tailed tests in hypothesis testing, with examples from A/B testing. Compare the advantages and disadvantages of each test type and when to use them.