whole numbers problem solving

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Understanding multiplication

Whole numbers

Here you will learn about whole numbers, including how to identify whole numbers, whole numbers on a number line, and the properties of whole numbers.

Students will first learn about whole numbers as part of counting and cardinality in Kindergarten and will expand their knowledge of whole numbers throughout elementary and middle school when learning about the properties of whole numbers and performing the four operations with whole numbers.

What are whole numbers?

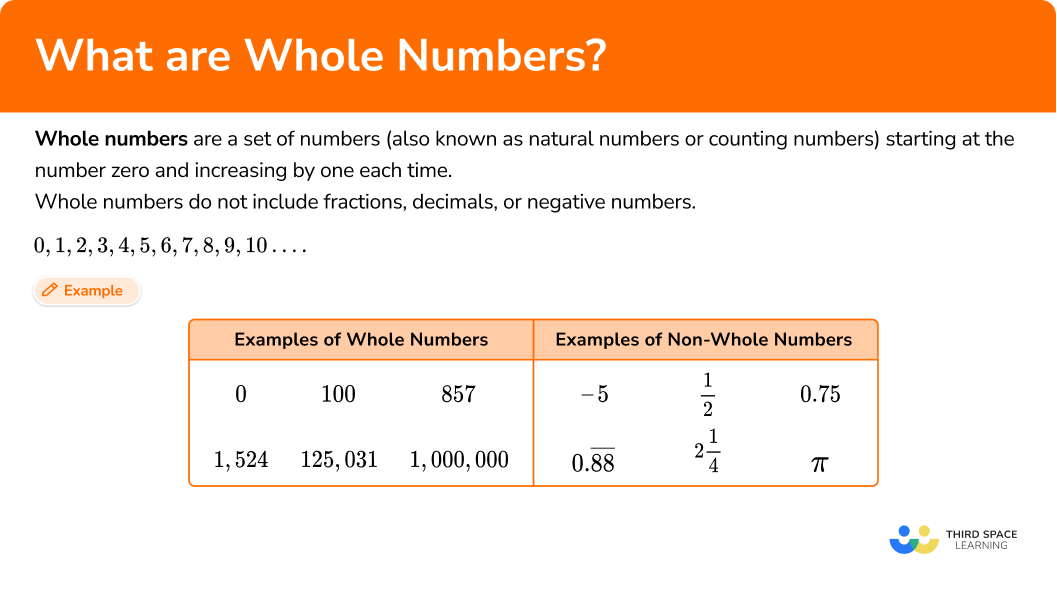
Whole numbers are a set of numbers starting at zero and increasing by one each time.

Whole numbers do not include fractions, decimals, or negative numbers. They are  positive integers.

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10….

All whole numbers are integers, but not all integers are whole numbers since integers also include negative numbers. Both whole numbers and integers are rational numbers.

For example,

Properties of whole numbers

Commutative property of whole numbers

• The commutative property of whole numbers states that the order of two numbers being added or multiplied together does not matter and that changing the order of the numbers will still give the same result.

See also : Commutative property

Associative property of whole numbers

• The associative property of whole numbers states that, when adding or multiplying three numbers, the grouping of two numbers within the expression can change and still give the same result.

See also : Associative property

Distributive property

• The distributive property of whole numbers says that multiplication is distributive over addition or subtraction. This means that when multiplying a number by a sum or difference of 2 numbers, you can multiply by each number separately and then add or subtract the products.

See also : Distributive property

Closure property

• The closure property of whole numbers says that the sum or product of two whole numbers will always be a whole number.

Common Core State Standards

How does this relate to Kindergarten math through 6th grade math?

• Kindergarten – Counting and Cardinality (K.CC.1, K.CC.2, K.CC.3) Count to 100 by ones and by tens; Count forward beginning from a given number within the known sequence (instead of having to begin at 1 ); Write numbers from 0 to 20. Represent a number of objects with a written numeral 0-20 (with 0 representing a count of no objects).
• Grade 1 – Operations and Algebraic Thinking (1.0A.B.3 ) Apply properties of operations as strategies to add and subtract. Examples: If 8 + 3 = 11 is known, then 3 + 8 = 11 is also known. (Commutative property of addition). To add 2 + 6 + 4, the second two numbers can be added to make a ten, so 2 + 6 + 4 = 2 + 10 = 12. (Associative property of addition).
• Grade 2 – Operations and Algebraic Thinking (2.OA.C.3) Determine whether a group of objects (up to 20 ) has an odd or even number of members, for example, by pairing objects or counting them by 2 s; write an equation to express an even number as a sum of two equal addends.
• Grade 3 – Operations and Algebraic Thinking (3.OA.B.5) Apply properties of operations as strategies to multiply and divide. Examples: If 6 \times 4 = 24 is known, then 4 \times 6 = 24 is also known. (Commutative property of multiplication). 3 \times 5 \times 2 can be found by 3 \times 5 = 15, then 15 \times 2 = 30, or by 5 \times 2 = 10, then 3 \times 10 = 30. (Associative property of multiplication). Knowing that 8 \times 5 = 40 and 8 \times 2 = 16, one can find 8 \times 7 as 8 \times (5 + 2) = (8 \times 5) + (8 \times 2) = 40 + 16 = 56. (Distributive property).
• Grade 4 – Number and Operations Base Ten (4.NBT.B.5) Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers, using strategies based on place value and the properties of operations. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
• Grade 6 – Number Systems (6.NS.B.4) Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1–100 with a common factor as a multiple of a sum of two whole numbers with no common factor. For example, express 36 + 8 as 4 \, (9 + 2).

How to use whole numbers

In order to identify whole numbers:

Recall the definition of the type of number needed.

Show whether the number fits or does not fit the definition.

In order to apply a property of whole numbers:

Recall the property.

Use the property to get an answer.

[FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)

Use this quiz to check your grade 6 students’ understanding of types of numbers. 10+ questions with answers covering a range of 2nd, 4th and 6th grade types of numbers topics to identify areas of strength and support!

Identifying whole numbers examples

Example 1: identifying whole numbers.

Which of the following are whole numbers?

0, \, 8.5, \, -1, \, 32, \, 6 \cfrac{1}{4} \, , \, 3.05, \, 927

Since the set of whole numbers does not include decimals, fractions, and negative numbers, you can eliminate 8.5, -1, 6 \cfrac{1}{4} \, , and 3.05 from the list.

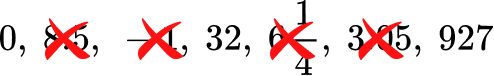
2 Show whether the number fits or does not fit the definition.

The remaining numbers are 0, 32, and 927. All three fit the definition and are whole numbers.

Answer: 0, 32, and 927

Example 2: identifying whole numbers

Maya says -4 is a whole number since it doesn’t have a decimal or fractional part. Is she correct?

The set of whole numbers includes all positive integers starting at zero. Whole numbers do not include negative numbers, fractions, or decimals.

-4 is not a whole number since it is not a positive number. Negative numbers are not whole numbers. Therefore, Maya is incorrect.

Example 3: identifying whole numbers

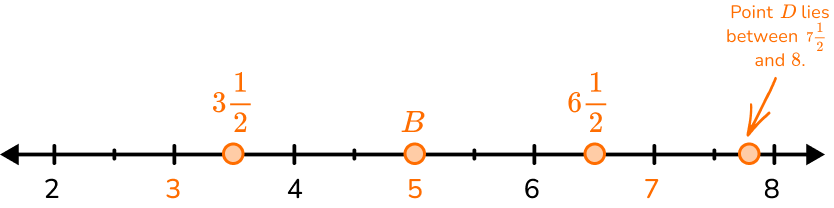
Which point on the number line represents a whole number?

The only point on the number line that shows a whole number is B, which represents 5.

Point A represents 3 \cfrac{1}{2} \, , point C represents 6 \cfrac{1}{2} \, and point D represents a fraction or decimal between 7 \cfrac{1}{2} and 8.

Since whole numbers do not include fractions or decimals, point B is the only whole number.

Example 4: identifying whole numbers

Which whole number fills in the blank in the sequence?

26, \, 27, \, 28, \, \rule{0.5cm}{0.15mm} \, , \, 30, \, 31

26, \, 27, \, 28, \, {\bf{29}}, \, 30, \, 31

Although there are many fractions and decimals in between 28 and 30, there is only one whole number, which is 29.

Example 5: apply a property of whole numbers

Fill in the blank using your knowledge of the commutative property of multiplication to make the equation true.

\rule{0.5cm}{0.15mm} \, \times 15=15 \times 3

The commutative property of multiplication states that the order of two numbers being multiplied together does not matter and that changing the order of the numbers will still give the same result.

a \times b = b \times a

\underline{3} \times 15=15 \times 3

The number 3 makes the equation true.

Example 6: apply a property of whole numbers

Fill in the blank using your knowledge of the distributive property to make the equation true.

3 \times(7 + 9)= \, \rule{0.5cm}{0.15mm} \, +27

The distributive property states that multiplication is distributive over addition. This means that when multiplying a number by a sum of 2 numbers, you can multiply by each number separately and then add the products.

a(b + c) =(a \times b) + (a \times c)

Since this equation can also be solved as (3 \times 7) + (3 \times 9), I know that the missing number is 21.

3 \times(7 + 9)=\underline{21}+27

Teaching tips for whole numbers

• Allow students to use concrete manipulatives to explore whole numbers when first building number sense.
• Use a number line to give students a visual representation of whole numbers. As they progress to higher grades, the number line can be partitioned into fractional and decimal parts as well, so students can see the difference between whole numbers and fractions/decimals. Later, a number line can also be extended past the number zero to show negative numbers. Students will gain better number sense when they are able to see non-examples of whole numbers.
• Display a chart or poster in the classroom showing the different types of numbers – whole numbers, natural numbers, integers, real numbers, etc. New types of numbers can be added to these displays in higher grade levels. This will help students differentiate between the sets of numbers.

Easy mistakes to make

• Thinking that zero is not a whole number Zero is the first and smallest whole number. The set of whole numbers begins at zero and increases by one with each number.
• Thinking that whole numbers are the same as integers Whole numbers are a subset of integers. Integers include all negative numbers, positive numbers, and zero, while whole numbers include only non-negative integers.

Related types of numbers lessons

This whole numbers topic guide is part of our series on types of numbers. You may find it helpful to start with the main types of numbers topic guide for a summary of what to expect or use the step-by-step guides below for further detail on individual topics. Other topic guides in this series include:

• Types of numbers
• Irrational numbers
• Rational numbers
• Prime numbers
• Natural numbers
• Prime and composite numbers
• Number sets
• Even numbers
• Odd numbers
• Absolute value

Practice identifying whole numbers questions

1. What is the smallest whole number?

The set of whole numbers starts at zero. Whole numbers do not include negative numbers, fractions, or decimals. Therefore, the smallest whole number listed is zero.

2. Look at the number line. What is the missing whole number?

When counting whole numbers by ones, the number after 19 will be 20.

3. Colin wrote a set of whole numbers on the whiteboard using the numbers 0, 1, 3, and 9. What number should he not have included?

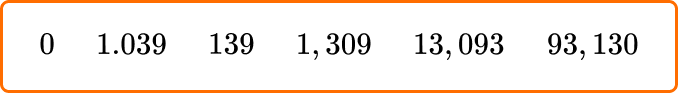
1.039 should not have been included because it is a decimal, not a whole number.

4. Select the group of numbers made up of only whole numbers.

101, \, 556, \, 18,000, \, 1 is the only group of numbers comprised of only whole numbers. The other groups include at least one fraction or decimal.

5. Which property is demonstrated by the following equation?

5(9+8)=(5 \times 9)+(5 \times 8)

Associative property

Commutative property

This shows the distributive property because multiplication is being distributed over addition. The distributive property allows you to perform the multiplication separately, then add the products.

6. Fill in the blank to make the equation true.

8 \times\left(6 \times \, \rule{0.5cm}{0.15mm} \, \right)=(8 \times 6) \times 4

This equation shows the associative property of multiplication, which states that when multiplying three numbers, the grouping of two numbers within the expression can change and still give the same result.

Therefore, since the right side shows 8, 6, and 4 being multiplied, I know the same 3 numbers are being multiplied on the left side of the equation.

Whole numbers FAQs

Whole numbers are a set of numbers (also known as natural numbers or counting numbers) starting at the number zero and increasing by one each time. Whole numbers do not include fractions, decimals, or negative numbers.

Whole numbers and natural numbers are very similar but not the same. The set of natural numbers starts at one instead of zero.

Whole numbers are a subset of integers. Integers include positive whole numbers, negative whole numbers, and zero, while whole numbers only include non-negative integers.

If the fraction has the same numerator and denominator, or if its numerator is a multiple of its denominator, it can be written as a whole number. For example, the fraction \cfrac{4}{2} can be written as the whole number 2.

The next lessons are

• Rounding numbers
• Factors and multiples

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (3rd to 8th Grade)

Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.

Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!

Privacy Overview

PRACTICE PROBLEMS ON WHOLE NUMBERS

Practice Problems on Whole Numbers :

In this section, we will see some practice problems on whole numbers.

(1)  The sum of two numbers is 90  and they are in the  ratio is 4:5. Find those numbers.

(A) 20 and 70                            (B) 40 and 50

(C) 35 and 55                            (D)  28 and 62

(2)  If the same numbers is added to both the numerator and denominator of a fraction 3/5, then the result is 3/4. Find the number.

(A) 3                                       (B) 4

(C) 5                                       (D)  8

(3)  Two numbers are such that the ratio between them is 5 : 7. When 7 is added to each of them, the ratio becomes 2 : 3. Find the numbers.

(A) 40 and 56                            (B) 10 and 14

(C) -35 and -49                         (D)  30 and 42

(4)  The sum of two numbers is 135 and they are in the ratio 7 : 8 . Find those numbers.

(A) 28 and 32                           (B)  35 and 40

(C) 63 and 72                           (D)  42 and 56

(5)  The difference of two numbers is 72 and the quotient obtained by dividing the one by other is 3. Find the numbers.

(A) 19 and 57                           (B)  36 and 108

(C) 163 and 72                          (D)  54 and 156

  Solution

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

Solving Trigonometric Equations Problems and Solutions

Dec 18, 24 10:53 AM

SAT Math Resources (Videos, Concepts, Worksheets and More)

Dec 17, 24 10:13 AM

Digital SAT Math Problems and Solutions (Part - 88)

Dec 17, 24 10:07 AM

Whole Numbers Questions

Whole numbers questions are provided here, along with detailed explanations, so that students can practise these questions to improve their understanding. These questions are helpful for the students of Class 6 since whole numbers is one of the important topics for them. However, in this grade, they will learn the basic properties of whole numbers and simple arithmetic operations to be performed on them. In this article, you will learn how to solve various problems on whole numbers in simple methods and get accurate answers.

What are whole numbers?

In mathematics, whole numbers are defined as the set of numbers that include positive integers and 0. In other words, whole numbers are comprised of natural numbers and 0. The set of whole numbers is denoted by the English alphabet W.

Thus, whole numbers = W = {0, 1, 2, 3, 4, 5, 6, 7,….}

Click here to get more information about whole numbers and the properties of whole numbers .

Whole Numbers Questions and Answers

1. Write the three whole numbers occurring just before 1001.

The three whole numbers occurring just before 1001 are 1000, 999 and 998.

2. How many whole numbers are there between 33 and 54?

The whole numbers between 33 and 54 are:

34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53

Thus, there are 20 whole numbers between 33 and 54.

3. Find the sum by suitable rearrangement.

197 + 234 + 103

This can be rearranged as:

(197 + 103) + 234

= 300 + 234

Therefore, 197 + 234 + 103 = 534.

4. The school canteen charges Rs. 20 for lunch and Rs. 4 for milk each day. How much money do you spend in 5 days on these things?

The cost of lunch per day = Rs. 20

The cost of milk per day = Rs. 4

Cost of lunch for 5 days = 5 × Rs. 20 = Rs. 100

Cost of milk for 5 days = 5 × Rs. 4 = Rs. 20

Total cost = Rs. (100 + 20) = Rs. 120

5. Simplify: 216 × 65 + 216 × 35.

216 × 65 + 216 × 35 = 216 × (65 + 35)

= 216 × 100

Thus, 216 × 65 + 216 × 35 = 21600

6. Find the product by suitable rearrangement:

(a) 2 × 1768 × 50

(b) 4 × 166 × 25

This expression can be rearranged as:

= (2 × 50) × 1768

= 100 × 1768

Therefore, 2 × 1768 × 50 = 176800

= (4 × 25) × 166

= 100 × 166

Therefore, 4 × 166 × 25 = 16600

7. A vendor supplies 32 litres of milk to a hotel in the morning and 68 litres in the evening. If the milk costs Rs. 45 per litre, how much money is due to the vendor per day?

Milk quantity supplied by a vendor in the morning = 32 litres

Milk quantity supplied by a vendor in the evening = 68 litres

The cost of milk per litre = Rs. 45

The total cost of milk per day = Rs. 45 × (32 + 68)

= Rs. 45 × 100

Therefore, the money due to the vendor per day is Rs. 4500.

8. Evaluate: 81265 × 249 – 81265 × 149.

81265 × 249 – 81265 × 149

= 81265 × (249 – 149)

= 81265 × 100

9. Find the product using suitable properties: 854 × 102.

= 854 × (100 + 2)

= 854 × 100 + 854 × 2 (Using distributive property)

= 85400 + 1708

Thus, 854 × 102 = 87108

10. Study the pattern:

1 × 8 + 1 = 9

12 × 8 + 2 = 98

123 × 8 + 3 = 987

1234 × 8 + 4 = 9876

12345 × 8 + 5 = 98765

Write the next two steps. Can you say how the pattern works?

(Hint: 12345 = 11111 + 1111 + 111 + 11 + 1).

From the given, we can write the next two steps as:

123456 × 8 + 6 = 987654

1234567 × 8 + 7 = 9876543

Using the pattern 12345 = 11111 + 1111 + 111 + 11 + 1, we have:

123456 = (111111 + 11111 + 1111 + 111 + 11 + 1)

123456 × 8 = (111111 + 11111 + 1111 + 111 + 11 + 1) × 8

= 111111 × 8 + 11111 × 8 + 1111 × 8 + 111 × 8 + 11 × 8 + 1 × 8

= 888888 + 88888 + 8888 + 888 + 88 + 8

123456 × 8 + 6 = 987648 + 6

Yes, here the pattern works.

Now, 1234567 × 8 + 7 = 9876543

1234567 = (1111111 + 111111 + 11111 + 1111 + 111 + 11 + 1)

1234567 × 8 = (1111111 + 111111 + 11111 + 1111 + 111 + 11 + 1) × 8

= 1111111 × 8 + 111111 × 8 + 11111 × 8 + 1111 × 8 + 111 × 8 + 11 × 8 + 1 × 8

= 8888888 + 888888 + 88888 + 8888 + 888 + 88 + 8

1234567 × 8 + 7 = 9876536 + 7

Yes, here also the pattern works.

Practice Questions on Whole Numbers

• Which is the smallest whole number?
• Evaluate the following using the distributive property of whole numbers. 4275 × 125
• Find the sum 1962 + 453 + 1538 + 647 using suitable rearrangement.
• Find the value of 24 + 27 + 16 in two different ways.
• Match the following:

(i) 425 × 136 = 425 × (6 + 30 +100) (a) Commutativity under multiplication.

(ii) 2 × 49 × 60 = 2 × 60 × 39 (b) Commutativity under addition.

(iii) 70 + 1005 + 30 = 70 + 30 + 1005 (c) Distributivity of multiplication over addition.

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Sixth Grade

• Whole numbers for grade 6 questions and Answers

" class="arrow-title-img"> Whole numbers for grade 6 questions and Answers

• Practice here
• Related contents

Get more contents on Whole numbers for grade 6 questions and Answers...

All practices skills about whole numbers for grade 6 questions and answers.

• Adding and subtracting whole numbers 6th grade
• Write numbers from words to digits in grade 6
• Write numbers from digits to words 6th grade online practice
• Roman numerals questions for 6th graders pupils
• Place Value and Names for Whole Numbers
• Write numbers from words in figures
• Spell word names for numbers up to one million

Free activities with simple ideas on how to solve operations with whole numbers in grade 6

All tutors and 6 th graders will enjoy practicing our free activities with simple ideas on solving operations with whole numbers in Grade 6. We have provided fun-solving tips and ideas, helpful for kids to fully engage in our whole numbers worksheets for Grade 6 pdf, free games online, lessons , word problems, etc.

Also, to make learning whole numbers fascinating and enjoyable for kids, we have designed our activities with beautiful colors and solving tips.

Most importantly, there is an easy-to-access answer guide, wherein kids can always refer to each time they want to do corrections.

WHAT’S THIS ALL ABOUT?

This is mathskills4kids.com a premium math quality website with original Math activities and other contents for math practice. We provide 100% free Math ressources for kids from Preschool to Grade 6 to improve learners skills.

Subtraction

Multiplication

Measurement

Telling Time

Problem Solving

Data & Graphs

Kindergarten

First Grade

Second Grade

Third Grade

Fourth Grade

Fifth Grade

SUBSCRIBE TO OUR NEWSLETTER

Privacy policy.

Our team Don't Pass on to third parties any identifiable information about mathskills4kids.com users. Your email address and other information will NEVER be given or sold to a third party.

USE OF CONTENTS

Many contents are released for free but you're not allowed to share content directly (we advise sharing website links), don't use these contents on another website or for a commercial issue. You're supposed to protect downloaded content and take it for personal or classroom use. Special rule : Teachers can use our content to teach in class.

Report a review

For more description, you can contact us here

We think you are located in South Africa . Is this correct?

• Yes, I reside in South Africa
• Change country/curriculum

We use this information to present the correct curriculum and to personalise content to better meet the needs of our users.

Solving problems with whole numbers

1.6 solving problems with whole numbers, order of operations.

If you use “BODMAS” or “BEDMAS” correctly to remember the order of operations, you will get the same answer. But, evaluating an expression using terms will help more with algebra later on!

Worked Example 1.22: Using order of operations in calculations

Do not use a calculator. Follow the correct order of operations to find the answer.

Separate the terms of the expression.

Thinking about “terms” is a useful way to help us to simplify. Terms are separated by addition and subtraction symbols, and joined into one by multiplication and division symbols, and brackets. To evaluate an expression, we must: separate it into terms simplify each term (if needed) add or subtract from left to right.

This expression has three terms: \(7\), \(−2 \times 1 \times 3\), and \(+3 \times 5\). We must simplify the second and third terms.

Add and subtract from left to right

Worked example 1.23: using order of operations in calculations, separate the expression into terms..

Remember that terms are separated by addition and subtraction symbols, and joined into one by multiplication and division symbols, and brackets. First separate into terms, then simplify, and then add or subtract from left to right.

This expression has three terms: \(19\), \(−5\), and \(+ 1^{2}\). We must simplify the exponent in the third term.

Simplify each term and calculate from left to right.

Instead of saying, for example “\(60\) calls per day”, people often say “at a rate of \(60\) calls per day”.

The word ‘per’ is often used to describe a rate and can mean for every , for , in each , in , out of , or every .

Speed is one example that describes the rate of movement over time. For example, a problem states that the invasive trees in the Western Cape are to be cut down in favour of natural vegetation. There are roughly \(3\ 000\ 000\) invasive trees in the area, and it is possible to cut them down at a rate of \(15\ 000\) trees per day with the labour available. The question could then be, “How many working days will it take before all the invasive trees have been cut down?”

To answer this rate question, you divide the total number of trees by the number that can be cut in one day:

So, it will take \(200\) days for all the trees to be cut down if the rate of cutting stays the same.

It is important to check that your answer makes sense. In this question we were looking for the number of days, so the answer must refer to days.

Worked Example 1.24: Solving problems with rate

A car travels a distance of \(180 \text{ km}\) in \(2\) hours on a straight road. How many kilometres can it travel in \(3\) hours at the same speed?

Understand the problem and summarise all the given information.

What we know:

• Distance = \(180 \text{ km}\)
• Time = \(2\) hours
• Speed = always the same

What we don’t know:

• Distance in \(3\) hours

Find the distance in \(1\) hour.

If the car travels \(180 \text{ km}\) in \(2\) hours, then it will travel \(180 \div 2 = 90 \text{ km}\) in \(1\) hour.

Find the distance in \(3\) hours (answer the question).

If the car travels \(90 \text{ km}\) in \(1\) hour, then it will travel \(90 \times 3 = 270 \text{ km}\) in \(3\) hours.

So, the car will travel \(270 \text{ km}\) in \(3\) hours.

Another useful concept is that of ratio . When we talk about ratio, we compare different amounts, such as the number of green apples and red apples in a bag, or the number of adults and children in a group. We might say, “there are two green apples for every red apple in the bag”, or “there are two children for every adult in the group”.

Look at these patterns.

Imagine if these are the beads and we continue the same pattern. In pattern A in the picture, there are \(5\) red beads for every \(4\) yellow beads. Try to describe patterns B and C in the same way.

You can either start with red beads or the yellow beads. It is equally correct to say “In pattern A there are \(4\) yellow beads for every \(5\) red beads.”

The patterns in question 4 can be described like this: In pattern A, the ratio of yellow beads to red beads is \(4\) to \(5\). This is written as \(4 : 5\). In pattern B, the ratio between yellow beads and red beads is \(3 : 6\). In pattern C the ratio is \(2 : 7\).

When solving problems with ratio, first look for the total number of parts. For example, in the pattern above, there are two parts: red beads and yellow beads. Then work out each quantity according to the ratio.

Worked Example 1.25: Dividing amounts in the given ratio

If the number of hours that Nathi, Modi and Tim worked are in the ratio \(5 : 4 : 3\), then to be fair, the payment should also be shared in that ratio. What fraction of the payment should each person get?

Work out the number that represents the total of the parts of the ratio.

Add the parts of the ratio: \(5 + 4 + 3 = 12\)

Write the ratio of each person’s payment as a fraction.

Nathi should receive \(5\) parts, Modi \(4\) parts, and Tim \(3\) parts of the money. There are \(12\) parts altogether, so of the total payment:

• Nathi should receive \(\frac{5}{12}\),
• Modi should get \(\frac{4}{12}\),
• and Tim should get \(\frac{3}{12}\).

Increasing and decreasing ratio

Sometimes you need to increase a ratio. For example, to increase \(40\) in the ratio \(2 : 3\) means that the \(40\) represents two parts and must be increased so that the new number represents \(3\) parts. If \(40\) represents two parts, then \(20\) represents \(1\) part. The increased number will therefore be \(20 \times 3 = 60\).

Worked Example 1.26: Increasing a number in the given ratio

Increase \(56\) in the ratio \(2 : 5\).

Find the number that represents \(1\) part.

If \(56\) represents \(2\) parts, then \(56 \div 2 = 28\) represents \(1\) part.

Find the number that represent the unknown ratio.

The second number in the ratio is \(5\), so \(28 \times 5 = 140\).

So, the increased number is \(140\).

Check your answer.

If the answer is correct, then \(56 : 140 = 2 : 5\).

Simplifying the ratio on the left-hand side should give us the ratio on the right-hand side.

When simplifying the ratio, you look for the highest common factor of both numbers. In this example, \(28\) is the highest common factor of \(56\) and \(140\).

Worked Example 1.27: Decreasing a number in the given ratio

Decrease \(30\) in a ratio of \(2 : 3\).

We are decreasing in a ratio of \(2 : 3\), so the answer must be smaller than \(30\). Therefore, \(30\) must be equivalent to the bigger part of the ratio.

This new ratio should be equivalent to the original ratio. So, both sides should be multiplied or divided by the same whole number.

If \(30\) represents \(3\) parts, then \(30 \div 3 = 10\) represents \(1\) part.

Find the number that represents the unknown ratio.

Our answer must be equivalent to the \(2\) part of the ratio.

Therefore, \(20 : 30\) is equivalent to \(2 : 3\).

\(30\) will decrease to \(20\).

Whole Number Word Problems

Singapore maths: primary 5 - whole numbers, word problem q1.

Singapore Math: Primary 5 - Whole Numbers, Word Problem Q2

Singapore Math: Primary 5 - Whole Numbers, Word Problem Q3

Singapore Maths: Primary 5 - Whole Numbers, Word Problem Q4

Next set of videos in this series

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.