design of experiments statistical test

JMP | Statistical Discovery.™ From SAS.

Statistics Knowledge Portal

A free online introduction to statistics

Design of experiments

What is design of experiments.

Design of experiments (DOE) is a systematic, efficient method that enables scientists and engineers to study the relationship between multiple input variables (aka factors) and key output variables (aka responses). It is a structured approach for collecting data and making discoveries.

When to use DOE?

• To determine whether a factor, or a collection of factors, has an effect on the response.
• To determine whether factors interact in their effect on the response.
• To model the behavior of the response as a function of the factors.
• To optimize the response.

Ronald Fisher first introduced four enduring principles of DOE in 1926: the factorial principle, randomization, replication and blocking. Generating and analyzing these designs relied primarily on hand calculation in the past; until recently practitioners started using computer-generated designs for a more effective and efficient DOE.

Why use DOE?

DOE is useful:

• In driving knowledge of cause and effect between factors.
• To experiment with all factors at the same time.
• To run trials that span the potential experimental region for our factors.
• In enabling us to understand the combined effect of the factors.

To illustrate the importance of DOE, let’s look at what will happen if DOE does NOT exist.

Experiments are likely to be carried out via trial and error or one-factor-at-a-time (OFAT) method.

Trial-and-error method

Test different settings of two factors and see what the resulting yield is.

Say we want to determine the optimal temperature and time settings that will maximize yield through experiments.

How the experiment looks like using trial-and-error method:

1. Conduct a trial at starting values for the two variables and record the yield:

2. Adjust one or both values based on our results:

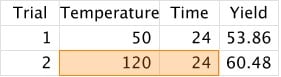
3. Repeat Step 2 until we think we've found the best set of values:

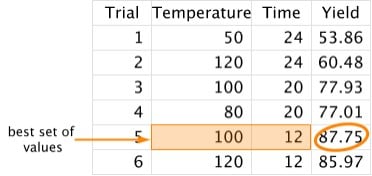
As you can tell, the  cons of trial-and-error  are:

• Inefficient, unstructured and ad hoc (worst if carried out without subject matter knowledge).
• Unlikely to find the optimum set of conditions across two or more factors.

One factor at a time (OFAT) method

Change the value of the one factor, then measure the response, repeat the process with another factor.

In the same experiment of searching optimal temperature and time to maximize yield, this is how the experiment looks using an OFAT method:

1. Start with temperature: Find the temperature resulting in the highest yield, between 50 and 120 degrees.

    1a. Run a total of eight trials. Each trial increases temperature by 10 degrees (i.e., 50, 60, 70 ... all the way to 120 degrees).

    1b. With time fixed at 20 hours as a controlled variable.

    1c. Measure yield for each batch.

2. Run the second experiment by varying time, to find the optimal value of time (between 4 and 24 hours).

    2a. Run a total of six trials. Each trial increases temperature by 4 hours (i.e., 4, 8, 12… up to 24 hours).

    2b. With temperature fixed at 90 degrees as a controlled variable.

    2c. Measure yield for each batch.

3. After a total of 14 trials, we’ve identified the max yield (86.7%) happens when:

• Temperature is at 90 degrees; Time is at 12 hours.

As you can already tell, OFAT is a more structured approach compared to trial and error.

But there’s one major problem with OFAT : What if the optimal temperature and time settings look more like this?

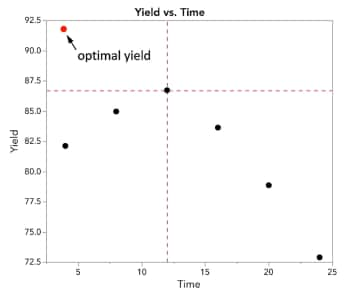
We would have missed out acquiring the optimal temperature and time settings based on our previous OFAT experiments.

Therefore,  OFAT’s con  is:

• We’re unlikely to find the optimum set of conditions across two or more factors.

How our trial and error and OFAT experiments look:

Notice that none of them has trials conducted at a low temperature and time AND near optimum conditions.

What went wrong in the experiments?

• We didn't simultaneously change the settings of both factors.
• We didn't conduct trials throughout the potential experimental region.

The result was a lack of understanding on the combined effect of the two variables on the response. The two factors did interact in their effect on the response!

A more effective and efficient approach to experimentation is to use statistically designed experiments (DOE).

Apply Full Factorial DOE on the same example

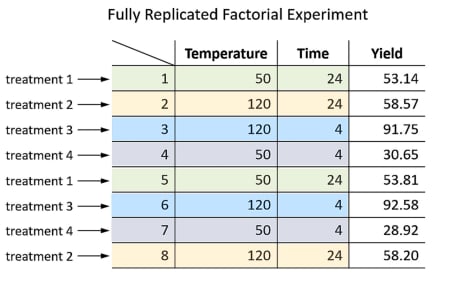
1. Experiment with two factors, each factor with two values. 

These four trials form the corners of the design space:

2. Run all possible combinations of factor levels, in random order to average out effects of lurking variables .

3. (Optional) Replicate entire design by running each treatment twice to find out experimental error :

4. Analyzing the results enable us to build a statistical model that estimates the individual effects (Temperature & Time), and also their interaction.

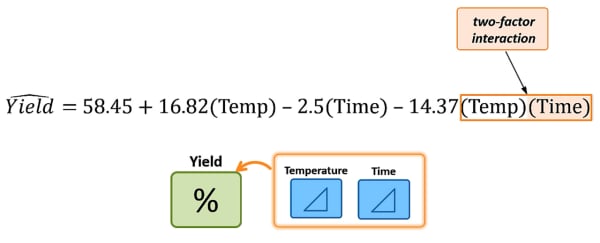
It enables us to visualize and explore the interaction between the factors. An illustration of what their interaction looks like at temperature = 120; time = 4:

You can visualize, explore your model and find the most desirable settings for your factors using the JMP Prediction Profiler .

Summary: DOE vs. OFAT/Trial-and-Error

• DOE requires fewer trials.
• DOE is more effective in finding the best settings to maximize yield.
• DOE enables us to derive a statistical model to predict results as a function of the two factors and their combined effect.

• Number System and Arithmetic
• Probability
• Mensuration
• Trigonometry
• Mathematics

Experimental Design

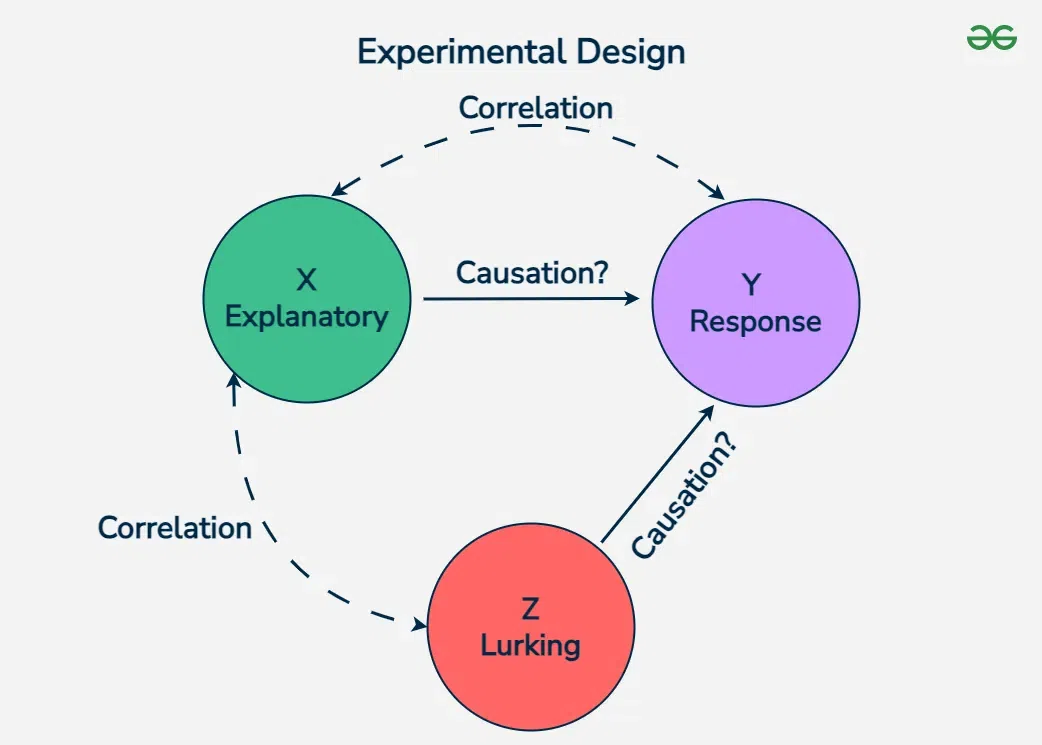
Experimental design is reviewed as an important part of the research methodology with an implication for the confirmation and reliability of the scientific studies. This is the scientific, logical and planned way of arranging tests and how they may be conducted so that hypotheses can be tested with the possibility of arriving at some conclusions. It refers to a procedure followed in order to control variables and conditions that may influence the outcome of a given study to reduce bias as well as improve the effectiveness of data collection and subsequently the quality of the results.

What is Experimental Design?

Experimental design simply refers to the strategy that is employed in conducting experiments to test hypotheses and arrive at valid conclusions. The process comprises firstly, the formulation of research questions, variable selection, specifications of the conditions for the experiment, and a protocol for data collection and analysis. The importance of experimental design can be seen through its potential to prevent bias, reduce variability, and increase the precision of results in an attempt to achieve high internal validity of studies. By using experimental design, the researchers can generate valid results which can be generalized in other settings which helps the advancement of knowledge in various fields.

Definition of Experimental Design

Experimental design is a systematic method of implementing experiments in which one can manipulate variables in a structured way in order to analyze hypotheses and draw outcomes based on empirical evidence.

Types of Experimental Design

Experimental design encompasses various approaches to conducting research studies, each tailored to address specific research questions and objectives. The primary types of experimental design include:

Pre-experimental Research Design

• True Experimental Research Design
• Quasi-Experimental Research Design

Statistical Experimental Design

A preliminary approach where groups are observed after implementing cause and effect factors to determine the need for further investigation. It is often employed when limited information is available or when researchers seek to gain initial insights into a topic. Pre-experimental designs lack random assignment and control groups, making it difficult to establish causal relationships.

Classifications:

• One-Shot Case Study
• One-Group Pretest-Posttest Design
• Static-Group Comparison

True-experimental Research Design

The true-experimental research design involves the random assignment of participants to experimental and control groups to establish cause-and-effect relationships between variables. It is used to determine the impact of an intervention or treatment on the outcome of interest. True-experimental designs satisfy the following factors: 

Factors to Satisfy:

• Random Assignment
• Control Group
• Experimental Group
• Pretest-Posttest Measures

Quasi-Experimental Design

A quasi-experimental design is an alternative to the true-experimental design when the random assignment of participants to the groups is not possible or desirable. It allows for comparisons between groups without random assignment, providing valuable insights into causal relationships in real-world settings. Quasi-experimental designs are used typically in conditions wherein the random assignment of the participants cannot be done or it may not be ethical, for example, an educational or community-based intervention.

Statistical experimental design, also known as design of experiments (DOE), is a branch of statistics that focuses on planning, conducting, analyzing, and interpreting controlled tests to evaluate the factors that may influence a particular outcome or process. The primary goal is to determine cause-and-effect relationships and to identify the optimal conditions for achieving desired results. The detailed is discussed below:

Design of Experiments: Goals & Settings

The goals and settings for design of experiments are as follows:

• Identifying Research Objectives: Clearly defining the goals and hypotheses of the experiment is crucial for designing an effective study.
• Selecting Appropriate Variables: Determining the independent, dependent, and control variables based on the research question.
• Considering Experimental Conditions: Identifying the settings and constraints under which the experiment will be conducted.
• Ensuring Validity and Reliability: Designing the experiment to minimize threats to internal and external validity.

Developing an Experimental Design

Developing an experimental design involves a systematic process of planning and structuring the study to achieve the research objectives. Here are the key steps:

• Define the research question and hypotheses
• Identify the independent and dependent variables
• Determine the experimental conditions and treatments
• Select the appropriate experimental design (e.g., completely randomized, randomized block, factorial)
• Determine the sample size and sampling method
• Establish protocols for data collection and analysis
• Conduct a pilot study to test the feasibility and refine the design
• Implement the experiment and collect data
• Analyze the data using appropriate statistical methods
• Interpret the results and draw conclusions

Preplanning, Defining, and Operationalizing for Design of Experiments

Preplanning, defining, and operationalizing are crucial steps in the design of experiments. Preplanning involves identifying the research objectives, selecting variables, and determining the experimental conditions. Defining refers to clearly stating the research question, hypotheses, and operational definitions of the variables. Operationalizing involves translating the conceptual definitions into measurable terms and establishing protocols for data collection.

For example, in a study investigating the effect of different fertilizers on plant growth, the researcher would preplan by selecting the independent variable (fertilizer type), dependent variable (plant height), and control variables (soil type, sunlight exposure). The research question would be defined as "Does the type of fertilizer affect the height of plants?" The operational definitions would include specific methods for measuring plant height and applying the fertilizers.

Randomized Block Design

Randomized block design is an experimental approach where subjects or units are grouped into blocks based on a known source of variability, such as location, time, or individual characteristics. The treatments are then randomly assigned to the units within each block. This design helps control for confounding factors, reduce experimental error, and increase the precision of estimates. By blocking, researchers can account for systematic differences between groups and focus on the effects of the treatments being studied

Consider a study investigating the effectiveness of two teaching methods (A and B) on student performance. The steps involved in a randomized block design would include:

• Identifying blocks based on student ability levels.
• Randomly assigning students within each block to either method A or B.
• Conducting the teaching interventions.
• Analyzing the results within each block to account for variability.

Completely Randomized Design

A completely randomized design is a straightforward experimental approach where treatments are randomly assigned to experimental units without any specific blocking. This design is suitable when there are no known sources of variability that need to be controlled for. In a completely randomized design, all units have an equal chance of receiving any treatment, and the treatments are distributed independently. This design is simple to implement and analyze but may be less efficient than a randomized block design when there are known sources of variability

Between-Subjects vs Within-Subjects Experimental Designs

Here is a detailed comparison among Between-Subject and Within-Subject is tabulated below:

Design of Experiments Examples

The examples of design experiments are as follows:

Between-Subjects Design Example:

In a study comparing the effectiveness of two teaching methods on student performance, one group of students (Group A) is taught using Method 1, while another group (Group B) is taught using Method 2. The performance of both groups is then compared to determine the impact of the teaching methods on student outcomes.

Within-Subjects Design Example:

In a study assessing the effects of different exercise routines on fitness levels, each participant undergoes all exercise routines over a period of time. Participants' fitness levels are measured before and after each routine to evaluate the impact of the exercises on their fitness levels.

Application of Experimental Design

The applications of Experimental design are as follows:

• Product Testing:  Experimental design is used to evaluate the effectiveness of new products or interventions.
• Medical Research:  It helps in testing the efficacy of treatments and interventions in controlled settings.
• Agricultural Studies:  Experimental design is crucial in testing new farming techniques or crop varieties.
• Psychological Experiments:  It is employed to study human behavior and cognitive processes.
• Quality Control:  Experimental design aids in optimizing processes and improving product quality.

In scientific research, experimental design is a crucial procedure that helps to outline an effective strategy for carrying out a meaningful experiment and making correct conclusions. This means that through proper control and coordination in conducting experiments, increased reliability and validity can be attained, and expansion of knowledge can take place generally across various fields. Using proper experimental design principles is crucial in ensuring that the experimental outcomes are impactful and valid.

Also, Check

• What is Hypothesis
• Null Hypothesis
• Real-life Applications of Hypothesis Testing

FAQs on Experimental Design

What is experimental design in math.

Experimental design refers to the aspect of planning experiments to gather data, decide the way in which to control the variable and draw sensible conclusions from the outcomes.

What are the advantages of the experimental method in math?

The advantages of the experimental method include control of variables, establishment of cause-and-effector relationship and use of statistical tools for proper data analysis.

What is the main purpose of experimental design?

The goal of experimental design is to describe the nature of variables and examine how changes in one or more variables impact the outcome of the experiment.

What are the limitations of experimental design?

Limitations include potential biases, the complexity of controlling all variables, ethical considerations, and the fact that some experiments can be costly or impractical.

What are the statistical tools used in experimental design?

Statistical tools utilized include ANOVA, regression analysis, t-tests, chi-square tests and factorial designs to conduct scientific research.

Similar Reads

• jQuery getJSON() Method In this article, we will learn about the getJSON() method in jQuery, along with understanding their implementation through the example. jQuery is an open-source JavaScript library that simplifies the interactions between an HTML/CSS document, It is widely famous for its philosophy of “Write less, do 2 min read
• How to open JSON file ? In this article, we will open the JSON file using JavaScript.  JSON stands for JavaScript Object Notation. It is basically a format for structuring data. The JSON format is a text-based format to represent the data in form of a JavaScript object. Approach: Create a JSON file, add data in that JSON f 2 min read
• How to open json file ? A JSON (JavaScript Object Notation) file is a standard format used to store and exchange data. Initially, JSON was primarily used for data transfer between web applications and servers, but its usage has expanded significantly. Today, JSON files are used for various purposes, including data backups 3 min read
• JSON Schema JSON Schema is a content specification language used for validating the structure of a JSON data.It helps you specify the objects and what values are valid inside the object's properties. JSON schema is useful in offering clear, human-readable, and machine-readable documentation. Structure of a JSON 2 min read
• What is JSON text ? The Javascript Object Notation(JSON) is used to transfer or exchange information on the internet. JSON is just the plain text written as a javascript object. There exist several key-value pairs which represent some useful information. The important thing to keep in mind is, although the JavaScript c 3 min read
• ES6 Merge Objects In this article, we are going to learn how to merge two objects in JavaScript. We can merge two JavaScript Objects in ES6 by using the two popular methods. The methods are listed below: Object.assign() methodObject spread syntax method Using Object.assign() method: Using this method, we can merge tw 3 min read
• How To Escape Strings in JSON? JSON (JavaScript Object Notation) is a popular data format that is widely used in APIs, configuration files, and data storage. While JSON is straightforward, handling special characters within strings requires some extra care. Certain characters must be escaped to be valid within a JSON string. Tabl 3 min read
• How to Handle Newlines in JSON? Handling newlines in JSON is essential for maintaining data integrity when dealing with multiline text. JSON, being a text-based format, requires special consideration for newlines to ensure that text appears as intended across different platforms. Proper handling of newlines ensures consistent and 2 min read
• Node.js querystring.encode() Function The querystring.encode() method is used to produce a URL query string from the given object that contains the key-value pairs. The method iterates through the object’s own properties to generate the query string. It can serialize a single or an array of strings, numbers, and boolean. Any other types 2 min read
• Rename Object Key in JavaScript In JavaScript, objects are used to store the collection of various data. It is a collection of properties. A property is a "key: value" pair where Keys are known as 'property name' and are used to identify values. Since JavaScript doesn't provide an inbuilt function to rename an object key. So we wi 4 min read
• String in JavaScript String is used to representing the sequence of characters. They are made up of a list of characters, which is essentially just an "array of characters". It can hold the data and manipulate the data which can be represented in the text form. We can perform different operations on strings like checkin 3 min read
• Add Nested JSON Object in Postman Postman is a helpful tool for testing APIs and working with JSON. It lets you add nested objects to existing JSON. JSON is a simple data format for both humans and machines. Postman also lets developers send requests and view responses, which is really useful for working with JSON data. These are th 2 min read
• Read, Write and Parse JSON using Python JSON is a lightweight data format for data interchange that can be easily read and written by humans, and easily parsed and generated by machines. It is a complete language-independent text format. To work with JSON data, Python has a built-in package called JSON. Example of JSON String s = '{"id":0 4 min read
• Deserializing a JSON into a JavaScript object Deserializing a JSON into a JavaScript object refers to the process of converting a JSON (JavaScript Object Notation) formatted string into a native JavaScript object. This allows developers to work with the data in JavaScript by accessing its properties and methods directly. JavaScript Object Notat 2 min read
• JavaScript JSON parse() Method The JSON.parse() method is used to convert a JSON string into a JavaScript object. It’s become important when dealing with data in JSON format, interacting with APIs, or storing data in the browser. It converts a JSON string into a JavaScript object.Throws a SyntaxError if the input string is not va 4 min read
• How to Receive JSON Data at Server Side ? JavaScript Object Notation (JSON) is a data transferring format used to send data to or from the server. It is commonly utilized in API integration due to its benefits and simplicity. In this example, we will utilize XML HttpRequest to deliver data to the server. Frontend: We will use a simple form 2 min read
• How to Convert String to Variable Name in JavaScript? In JavaScript, if we consider the variable names as string values, it is difficult to transform a variable’s name into a string. However, this problem has been handled in many ways for example, static properties of objects, eval(), and modern ways such as Map can be used to achieve the essential eff 3 min read
• How to Pass Object as Parameter in JavaScript ? We'll see how to Pass an object as a Parameter in JavaScript. We can pass objects as parameters to functions just like we do with any other data type. passing objects as parameters to functions allows us to manipulate their properties within the function. These are the following approaches: Table of 3 min read
• JavaScript JSON Parser JSON (JavaScript Object Notation) is a popular lightweight data exchange format for sending data between a server and a client, or across various systems. JSON data is parsed and interpreted using a software component or library called a JSON parser. Through the JSON parsing process, a JSON string i 3 min read
• School Learning
• Math-Statistics

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Design of Experiments - DoE

Design of Experiments, or DoE, is a systematic approach to planning, conducting, and analyzing experiments.

The goal of Design of Experiments is to explore how various input variables, called factors, affect an output variable, known as the response. In more complex systems, there may also be multiple responses to analyze.

Depending on the field of study, the system being investigated could be a process, a machine, or a product. But it can also be a human being, for example, when studying the effects of medication.

Each factor has multiple levels. For example, the factor 'lubrication' might have levels such as oil and grease, while the factor 'temperature' could have levels like low, medium, and high.

These are the input variables or parameters that are changed or manipulated in the experiment. Each factor can have different levels, which represent the different values it can take.

Examples: temperature, pressure, material type, machine speed.

These are the specific values that a factor can take in an experiment.

Examples: For the factor "temperature," the levels could be 100°C, 150°C, and 200°C.

Response (or Output)

This is the measured outcome or result that changes in response to the factors being manipulated.

Examples: yield, strength, time to failure, customer satisfaction.

When is a DoE used?

There are two primary applications of Design of Experiments (DOE): the first is to identify the key influencing factors, determining which factors have a significant impact on the outcome. The second is to optimize the input variables, aiming to either minimize or maximize the response, depending on the desired result.

Different experimental designs are selected based on the objective: screening designs are used to identify significant factors, while optimization designs are employed to determine the optimal input variables.

Screening Designs

Screening Designs are used early in an experiment to identify the most important factors from a larger set of potential variables. These designs, such as Fractional Factorial Designs or Plackett-Burman Designs, focus on determining which factors have a significant effect on the response, often with a reduced number of runs.

Optimization Designs

Optimization Designs, on the other hand, are used after the important factors have been identified. These designs are used to refine and optimize the levels of the significant factors to achieve an ideal response. Common examples include: full factorial designs , central composite designs (CCD), and Box-Behnken designs (BBD).

The DoE Process

Of course, both steps can be carried out sequentially. Let's take a look at the process of a DoE project: planning, screening, optimization, and verification.

The first step, planning, involves three key tasks:

• 1) Gaining a clear understanding of the problem or system.
• 2) Identifying one or more responses.
• 3) Determining the factors that could significantly influence the response.

Identifying potential factors that influence the response can be quite complex and time-consuming. For this, an Ishikawa diagram can be created by the team.

Screening Design

The second step is Screening. If there are many factors that could have an influence (typically more than 4-6 factors), screening experiments should be conducted to reduce the number of factors.

Why is this important? The number of factors to be studied has a major impact on the number of experiments required.

In a full factorial design, the number of experiments is determined by n = 2 raised to the power of k, where n is the number of experiments, and k is the number of factors. Here's a small overview: if we have three factors, at least 8 experiments are required; for 7 factors, at least 128 experiments are needed, and for 10 factors, at least 1024 experiments are required.

Note that this table applies to a design where each factor has only two levels; otherwise, more experiments will be needed.

Depending on how complex each experiment is, it may be worthwhile to choose screening designs when there are 4 or more factors. Screening designs include fractional factorial designs and the Plackett-Burman design.

Once significant factors have been identified using screening experiments, and the number of factors has hopefully been reduced, further experiments can be conducted.

The obtained data can then be used to create a regression model, which helps determine the input variables that optimize the response.

Verification

After optimization, the final step is verification. Here, it is tested once again whether the calculated optimal input variables actually have the desired effect on the response!

Detailed Steps in Conducting DOE

Problem Definition: Clearly define the objective of the experiment. Identify the response variable and the factors that may affect it.

Select Factors, Levels, and Ranges: Determine the factors that will be studied and the specific levels at which each factor will be set. Consider practical constraints and prior knowledge.

Choose an Experimental Design: Select an appropriate design based on the number of factors, the complexity of the interactions, and resource availability (time, cost).

Conduct the Experiment: Perform the experiment according to the design. It is essential to randomize the order of the experimental runs to avoid systematic errors.

Collect Data: Gather data on the response variable for each experimental run.

Analyze the Data: Use statistical methods such as analysis of variance (ANOVA), regression, or specialized DOE software to analyze the results. The goal is to understand the effects of factors and their interactions on the response.

Draw Conclusions and Make Decisions: Based on the analysis, draw conclusions about which factors are significant, how they interact, and how the process or product can be optimized.

Validate the Results: Confirm the findings by conducting additional experiments or applying the findings to real-world situations. Validation ensures that the conclusions are generalizable.

Examples of Experimental Designs

There are various experimental designs, and here are some of the most common ones, which can easily be calculated using the DoE software DATAtab .

Full Factorial Designs : These designs test all possible combinations of the factors and provide detailed information about main effects and interactions.

Fractional Factorial Designs : These designs use only a fraction of the possible combinations to increase efficiency while still obtaining essential information.

Plackett-Burman Designs: A screening design that aims to quickly identify which factors have the greatest effect.

Response Surface Designs: These include, for example, Central Composite Designs (CCD), which are used to find optimal settings, especially in cases where there are nonlinear relationships between factors and the response.

Key Aspects of Experimental Design

Efficiency: DoE helps gather as much information as possible with a minimal number of experiments. This is especially important when experiments are expensive or time-consuming. Instead of testing all possible combinations of factors (as in full factorial designs), statistical methods can significantly reduce the number of experiments without losing essential information.

Factor Effects and Interactions: In an experiment, multiple factors often influence the result simultaneously. Experimental design allows for the analysis of isolated effects of these factors and their interactions. Interactions occur when the simultaneous change of several factors has a greater effect on the outcome than the sum of their individual effects.

Creating a DoE with DATAtab

Of course you can create a test plan with DATAtab. To do this, simply click here: Create DoE online .

You can choose from a variety of designs and then specify the number of factors. The experimental plan created is then displayed.

Statistics made easy

• many illustrative examples
• ideal for exams and theses
• statistics made easy on 412 pages
• 5rd revised edition (April 2024)
• Only 8.99 €

"Super simple written"

"It could not be simpler"

"So many helpful examples"

Cite DATAtab: DATAtab Team (2024). DATAtab: Online Statistics Calculator. DATAtab e.U. Graz, Austria. URL https://datatab.net

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

Lesson 1: introduction to design of experiments, overview section  .

In this course we will pretty much cover the textbook - all of the concepts and designs included. I think we will have plenty of examples to look at and experience to draw from.

Please note: the main topics listed in the syllabus follow the chapters in the book.

A word of advice regarding the analyses. The prerequisite for this course is STAT 501 - Regression Methods and STAT 502 - Analysis of Variance . However, the focus of the course is on the design and not on the analysis. Thus, one can successfully complete this course without these prerequisites, with just STAT 500 - Applied Statistics for instance, but it will require much more work, and for the analysis less appreciation of the subtleties involved. You might say it is more conceptual than it is math oriented.

  Text Reference: Montgomery, D. C. (2019). Design and Analysis of Experiments , 10th Edition, John Wiley & Sons. ISBN 978-1-119-59340-9

What is the Scientific Method? Section  

Do you remember learning about this back in high school or junior high even? What were those steps again?

Decide what phenomenon you wish to investigate. Specify how you can manipulate the factor and hold all other conditions fixed, to insure that these extraneous conditions aren't influencing the response you plan to measure.

Then measure your chosen response variable at several (at least two) settings of the factor under study. If changing the factor causes the phenomenon to change, then you conclude that there is indeed a cause-and-effect relationship at work.

How many factors are involved when you do an experiment? Some say two - perhaps this is a comparative experiment? Perhaps there is a treatment group and a control group? If you have a treatment group and a control group then, in this case, you probably only have one factor with two levels.

How many of you have baked a cake? What are the factors involved to ensure a successful cake? Factors might include preheating the oven, baking time, ingredients, amount of moisture, baking temperature, etc.-- what else? You probably follow a recipe so there are many additional factors that control the ingredients - i.e., a mixture. In other words, someone did the experiment in advance! What parts of the recipe did they vary to make the recipe a success? Probably many factors, temperature and moisture, various ratios of ingredients, and presence or absence of many additives.  Now, should one keep all the factors involved in the experiment at a constant level and just vary one to see what would happen?  This is a strategy that works but is not very efficient.  This is one of the concepts that we will address in this course.

• understand the issues and principles of Design of Experiments (DOE),
• understand experimentation is a process,
• list the guidelines for designing experiments, and
• recognize the key historical figures in DOE.

LEARN STATISTICS EASILY

Learn Data Analysis Now!

What is: Design Of Experiments

What is design of experiments.

Design of Experiments (DOE) is a systematic method used to determine the relationship between factors affecting a process and the output of that process. It is a crucial aspect of statistical analysis, allowing researchers and analysts to plan, conduct, and analyze experiments efficiently. By employing DOE, one can optimize processes and improve product quality while minimizing costs and time.

Ad description. Lorem ipsum dolor sit amet, consectetur adipiscing elit.

Importance of Design Of Experiments

The significance of Design of Experiments lies in its ability to provide a structured approach to experimentation. It helps in identifying the critical factors that influence outcomes, enabling data scientists and statisticians to make informed decisions. DOE is widely used in various fields, including agriculture, manufacturing, and pharmaceuticals, to enhance product development and process optimization.

Key Components of Design Of Experiments

There are several key components in the Design of Experiments framework, including factors, levels, and responses. Factors are the independent variables that are manipulated during the experiment, while levels refer to the specific values or settings of these factors. Responses are the dependent variables that are measured to assess the impact of the factors. Understanding these components is essential for effective experimental design.

Types of Design Of Experiments

There are various types of Design of Experiments, including full factorial designs, fractional factorial designs, and response surface methodologies. Full factorial designs involve testing all possible combinations of factors and levels, providing comprehensive insights. Fractional factorial designs, on the other hand, test only a subset of combinations, making them more efficient for large experiments. Response surface methodologies focus on optimizing responses by exploring the relationships between factors.

Steps in Conducting Design Of Experiments

Conducting a Design of Experiments involves several critical steps. First, one must define the objective of the experiment and identify the factors and levels to be tested. Next, a suitable experimental design is selected, followed by the execution of the experiment. Data collection and analysis are then performed, leading to the interpretation of results and conclusions drawn from the findings.

Statistical Analysis in Design Of Experiments

Statistical analysis plays a vital role in the Design of Experiments. Techniques such as Analysis of Variance (ANOVA) are commonly used to determine the significance of factors and interactions. By analyzing the data collected from experiments, researchers can identify which factors have the most substantial impact on the response variable, allowing for better decision-making and process improvements.

Applications of Design Of Experiments

Design of Experiments is applied across various industries for numerous purposes. In manufacturing, it is used to optimize production processes and enhance product quality. In pharmaceuticals, DOE helps in drug formulation and testing. Additionally, in agriculture, it aids in determining the best conditions for crop yield. The versatility of DOE makes it an invaluable tool in research and development.

Challenges in Design Of Experiments

Despite its advantages, Design of Experiments can present challenges. These include the complexity of designing experiments, the need for statistical expertise, and potential resource constraints. Additionally, ensuring the reliability and validity of results can be difficult, especially in real-world applications where numerous variables may interact in unpredictable ways.

Future Trends in Design Of Experiments

The future of Design of Experiments is likely to be influenced by advancements in technology and data analytics. The integration of machine learning and artificial intelligence into DOE processes can enhance the efficiency and accuracy of experiments. Furthermore, the growing emphasis on big data will enable more comprehensive analyses, leading to better insights and innovations in various fields.

Statistical Design and Analysis of Biological Experiments

Chapter 1 principles of experimental design, 1.1 introduction.

The validity of conclusions drawn from a statistical analysis crucially hinges on the manner in which the data are acquired, and even the most sophisticated analysis will not rescue a flawed experiment. Planning an experiment and thinking about the details of data acquisition is so important for a successful analysis that R. A. Fisher—who single-handedly invented many of the experimental design techniques we are about to discuss—famously wrote

To call in the statistician after the experiment is done may be no more than asking him to perform a post-mortem examination: he may be able to say what the experiment died of. ( Fisher 1938 )

(Statistical) design of experiments provides the principles and methods for planning experiments and tailoring the data acquisition to an intended analysis. Design and analysis of an experiment are best considered as two aspects of the same enterprise: the goals of the analysis strongly inform an appropriate design, and the implemented design determines the possible analyses.

The primary aim of designing experiments is to ensure that valid statistical and scientific conclusions can be drawn that withstand the scrutiny of a determined skeptic. Good experimental design also considers that resources are used efficiently, and that estimates are sufficiently precise and hypothesis tests adequately powered. It protects our conclusions by excluding alternative interpretations or rendering them implausible. Three main pillars of experimental design are randomization , replication , and blocking , and we will flesh out their effects on the subsequent analysis as well as their implementation in an experimental design.

An experimental design is always tailored towards predefined (primary) analyses and an efficient analysis and unambiguous interpretation of the experimental data is often straightforward from a good design. This does not prevent us from doing additional analyses of interesting observations after the data are acquired, but these analyses can be subjected to more severe criticisms and conclusions are more tentative.

In this chapter, we provide the wider context for using experiments in a larger research enterprise and informally introduce the main statistical ideas of experimental design. We use a comparison of two samples as our main example to study how design choices affect an analysis, but postpone a formal quantitative analysis to the next chapters.

1.2 A Cautionary Tale

For illustrating some of the issues arising in the interplay of experimental design and analysis, we consider a simple example. We are interested in comparing the enzyme levels measured in processed blood samples from laboratory mice, when the sample processing is done either with a kit from a vendor A, or a kit from a competitor B. For this, we take 20 mice and randomly select 10 of them for sample preparation with kit A, while the blood samples of the remaining 10 mice are prepared with kit B. The experiment is illustrated in Figure 1.1 A and the resulting data are given in Table 1.1 .

One option for comparing the two kits is to look at the difference in average enzyme levels, and we find an average level of 10.32 for vendor A and 10.66 for vendor B. We would like to interpret their difference of -0.34 as the difference due to the two preparation kits and conclude whether the two kits give equal results or if measurements based on one kit are systematically different from those based on the other kit.

Such interpretation, however, is only valid if the two groups of mice and their measurements are identical in all aspects except the sample preparation kit. If we use one strain of mice for kit A and another strain for kit B, any difference might also be attributed to inherent differences between the strains. Similarly, if the measurements using kit B were conducted much later than those using kit A, any observed difference might be attributed to changes in, e.g., mice selected, batches of chemicals used, device calibration, or any number of other influences. None of these competing explanations for an observed difference can be excluded from the given data alone, but good experimental design allows us to render them (almost) arbitrarily implausible.

A second aspect for our analysis is the inherent uncertainty in our calculated difference: if we repeat the experiment, the observed difference will change each time, and this will be more pronounced for a smaller number of mice, among others. If we do not use a sufficient number of mice in our experiment, the uncertainty associated with the observed difference might be too large, such that random fluctuations become a plausible explanation for the observed difference. Systematic differences between the two kits, of practically relevant magnitude in either direction, might then be compatible with the data, and we can draw no reliable conclusions from our experiment.

In each case, the statistical analysis—no matter how clever—was doomed before the experiment was even started, while simple ideas from statistical design of experiments would have provided correct and robust results with interpretable conclusions.

1.3 The Language of Experimental Design

By an experiment we understand an investigation where the researcher has full control over selecting and altering the experimental conditions of interest, and we only consider investigations of this type. The selected experimental conditions are called treatments . An experiment is comparative if the responses to several treatments are to be compared or contrasted. The experimental units are the smallest subdivision of the experimental material to which a treatment can be assigned. All experimental units given the same treatment constitute a treatment group . Especially in biology, we often compare treatments to a control group to which some standard experimental conditions are applied; a typical example is using a placebo for the control group, and different drugs for the other treatment groups.

The values observed are called responses and are measured on the response units ; these are often identical to the experimental units but need not be. Multiple experimental units are sometimes combined into groupings or blocks , such as mice grouped by litter, or samples grouped by batches of chemicals used for their preparation. More generally, we call any grouping of the experimental material (even with group size one) a unit .

In our example, we selected the mice, used a single sample per mouse, deliberately chose the two specific vendors, and had full control over which kit to assign to which mouse. In other words, the two kits are the treatments and the mice are the experimental units. We took the measured enzyme level of a single sample from a mouse as our response, and samples are therefore the response units. The resulting experiment is comparative, because we contrast the enzyme levels between the two treatment groups.

Figure 1.1: Three designs to determine the difference between two preparation kits A and B based on four mice. A: One sample per mouse. Comparison between averages of samples with same kit. B: Two samples per mouse treated with the same kit. Comparison between averages of mice with same kit requires averaging responses for each mouse first. C: Two samples per mouse each treated with different kit. Comparison between two samples of each mouse, with differences averaged.

In this example, we can coalesce experimental and response units, because we have a single response per mouse and cannot distinguish a sample from a mouse in the analysis, as illustrated in Figure 1.1 A for four mice. Responses from mice with the same kit are averaged, and the kit difference is the difference between these two averages.

By contrast, if we take two samples per mouse and use the same kit for both samples, then the mice are still the experimental units, but each mouse now groups the two response units associated with it. Now, responses from the same mouse are first averaged, and these averages are used to calculate the difference between kits; even though eight measurements are available, this difference is still based on only four mice (Figure 1.1 B).

If we take two samples per mouse, but apply each kit to one of the two samples, then the samples are both the experimental and response units, while the mice are blocks that group the samples. Now, we calculate the difference between kits for each mouse, and then average these differences (Figure 1.1 C).

If we only use one kit and determine the average enzyme level, then this investigation is still an experiment, but is not comparative.

To summarize, the design of an experiment determines the logical structure of the experiment ; it consists of (i) a set of treatments (the two kits); (ii) a specification of the experimental units (animals, cell lines, samples) (the mice in Figure 1.1 A,B and the samples in Figure 1.1 C); (iii) a procedure for assigning treatments to units; and (iv) a specification of the response units and the quantity to be measured as a response (the samples and associated enzyme levels).

1.4 Experiment Validity

Before we embark on the more technical aspects of experimental design, we discuss three components for evaluating an experiment’s validity: construct validity , internal validity , and external validity . These criteria are well-established in areas such as educational and psychological research, and have more recently been discussed for animal research ( Würbel 2017 ) where experiments are increasingly scrutinized for their scientific rationale and their design and intended analyses.

1.4.1 Construct Validity

Construct validity concerns the choice of the experimental system for answering our research question. Is the system even capable of providing a relevant answer to the question?

Studying the mechanisms of a particular disease, for example, might require careful choice of an appropriate animal model that shows a disease phenotype and is accessible to experimental interventions. If the animal model is a proxy for drug development for humans, biological mechanisms must be sufficiently similar between animal and human physiologies.

Another important aspect of the construct is the quantity that we intend to measure (the measurand ), and its relation to the quantity or property we are interested in. For example, we might measure the concentration of the same chemical compound once in a blood sample and once in a highly purified sample, and these constitute two different measurands, whose values might not be comparable. Often, the quantity of interest (e.g., liver function) is not directly measurable (or even quantifiable) and we measure a biomarker instead. For example, pre-clinical and clinical investigations may use concentrations of proteins or counts of specific cell types from blood samples, such as the CD4+ cell count used as a biomarker for immune system function.

1.4.2 Internal Validity

The internal validity of an experiment concerns the soundness of the scientific rationale, statistical properties such as precision of estimates, and the measures taken against risk of bias. It refers to the validity of claims within the context of the experiment. Statistical design of experiments plays a prominent role in ensuring internal validity, and we briefly discuss the main ideas before providing the technical details and an application to our example in the subsequent sections.

Scientific Rationale and Research Question

The scientific rationale of a study is (usually) not immediately a statistical question. Translating a scientific question into a quantitative comparison amenable to statistical analysis is no small task and often requires careful consideration. It is a substantial, if non-statistical, benefit of using experimental design that we are forced to formulate a precise-enough research question and decide on the main analyses required for answering it before we conduct the experiment. For example, the question: is there a difference between placebo and drug? is insufficiently precise for planning a statistical analysis and determine an adequate experimental design. What exactly is the drug treatment? What should the drug’s concentration be and how is it administered? How do we make sure that the placebo group is comparable to the drug group in all other aspects? What do we measure and what do we mean by “difference?” A shift in average response, a fold-change, change in response before and after treatment?

The scientific rationale also enters the choice of a potential control group to which we compare responses. The quote

The deep, fundamental question in statistical analysis is ‘Compared to what?’ ( Tufte 1997 )

highlights the importance of this choice.

There are almost never enough resources to answer all relevant scientific questions. We therefore define a few questions of highest interest, and the main purpose of the experiment is answering these questions in the primary analysis . This intended analysis drives the experimental design to ensure relevant estimates can be calculated and have sufficient precision, and tests are adequately powered. This does not preclude us from conducting additional secondary analyses and exploratory analyses , but we are not willing to enlarge the experiment to ensure that strong conclusions can also be drawn from these analyses.

Risk of Bias

Experimental bias is a systematic difference in response between experimental units in addition to the difference caused by the treatments. The experimental units in the different groups are then not equal in all aspects other than the treatment applied to them. We saw several examples in Section 1.2 .

Minimizing the risk of bias is crucial for internal validity and we look at some common measures to eliminate or reduce different types of bias in Section 1.5 .

Precision and Effect Size

Another aspect of internal validity is the precision of estimates and the expected effect sizes. Is the experimental setup, in principle, able to detect a difference of relevant magnitude? Experimental design offers several methods for answering this question based on the expected heterogeneity of samples, the measurement error, and other sources of variation: power analysis is a technique for determining the number of samples required to reliably detect a relevant effect size and provide estimates of sufficient precision. More samples yield more precision and more power, but we have to be careful that replication is done at the right level: simply measuring a biological sample multiple times as in Figure 1.1 B yields more measured values, but is pseudo-replication for analyses. Replication should also ensure that the statistical uncertainties of estimates can be gauged from the data of the experiment itself, without additional untestable assumptions. Finally, the technique of blocking , shown in Figure 1.1 C, can remove a substantial proportion of the variation and thereby increase power and precision if we find a way to apply it.

1.4.3 External Validity

The external validity of an experiment concerns its replicability and the generalizability of inferences. An experiment is replicable if its results can be confirmed by an independent new experiment, preferably by a different lab and researcher. Experimental conditions in the replicate experiment usually differ from the original experiment, which provides evidence that the observed effects are robust to such changes. A much weaker condition on an experiment is reproducibility , the property that an independent researcher draws equivalent conclusions based on the data from this particular experiment, using the same analysis techniques. Reproducibility requires publishing the raw data, details on the experimental protocol, and a description of the statistical analyses, preferably with accompanying source code. Many scientific journals subscribe to reporting guidelines to ensure reproducibility and these are also helpful for planning an experiment.

A main threat to replicability and generalizability are too tightly controlled experimental conditions, when inferences only hold for a specific lab under the very specific conditions of the original experiment. Introducing systematic heterogeneity and using multi-center studies effectively broadens the experimental conditions and therefore the inferences for which internal validity is available.

For systematic heterogeneity , experimental conditions are systematically altered in addition to the treatments, and treatment differences estimated for each condition. For example, we might split the experimental material into several batches and use a different day of analysis, sample preparation, batch of buffer, measurement device, and lab technician for each batch. A more general inference is then possible if effect size, effect direction, and precision are comparable between the batches, indicating that the treatment differences are stable over the different conditions.

In multi-center experiments , the same experiment is conducted in several different labs and the results compared and merged. Multi-center approaches are very common in clinical trials and often necessary to reach the required number of patient enrollments.

Generalizability of randomized controlled trials in medicine and animal studies can suffer from overly restrictive eligibility criteria. In clinical trials, patients are often included or excluded based on co-medications and co-morbidities, and the resulting sample of eligible patients might no longer be representative of the patient population. For example, Travers et al. ( 2007 ) used the eligibility criteria of 17 random controlled trials of asthma treatments and found that out of 749 patients, only a median of 6% (45 patients) would be eligible for an asthma-related randomized controlled trial. This puts a question mark on the relevance of the trials’ findings for asthma patients in general.

1.5 Reducing the Risk of Bias

1.5.1 randomization of treatment allocation.

If systematic differences other than the treatment exist between our treatment groups, then the effect of the treatment is confounded with these other differences and our estimates of treatment effects might be biased.

We remove such unwanted systematic differences from our treatment comparisons by randomizing the allocation of treatments to experimental units. In a completely randomized design , each experimental unit has the same chance of being subjected to any of the treatments, and any differences between the experimental units other than the treatments are distributed over the treatment groups. Importantly, randomization is the only method that also protects our experiment against unknown sources of bias: we do not need to know all or even any of the potential differences and yet their impact is eliminated from the treatment comparisons by random treatment allocation.

Randomization has two effects: (i) differences unrelated to treatment become part of the ‘statistical noise’ rendering the treatment groups more similar; and (ii) the systematic differences are thereby eliminated as sources of bias from the treatment comparison.

Randomization transforms systematic variation into random variation.

In our example, a proper randomization would select 10 out of our 20 mice fully at random, such that the probability of any one mouse being picked is 1/20. These ten mice are then assigned to kit A, and the remaining mice to kit B. This allocation is entirely independent of the treatments and of any properties of the mice.

To ensure random treatment allocation, some kind of random process needs to be employed. This can be as simple as shuffling a pack of 10 red and 10 black cards or using a software-based random number generator. Randomization is slightly more difficult if the number of experimental units is not known at the start of the experiment, such as when patients are recruited for an ongoing clinical trial (sometimes called rolling recruitment ), and we want to have reasonable balance between the treatment groups at each stage of the trial.

Seemingly random assignments “by hand” are usually no less complicated than fully random assignments, but are always inferior. If surprising results ensue from the experiment, such assignments are subject to unanswerable criticism and suspicion of unwanted bias. Even worse are systematic allocations; they can only remove bias from known causes, and immediately raise red flags under the slightest scrutiny.

The Problem of Undesired Assignments

Even with a fully random treatment allocation procedure, we might end up with an undesirable allocation. For our example, the treatment group of kit A might—just by chance—contain mice that are all bigger or more active than those in the other treatment group. Statistical orthodoxy recommends using the design nevertheless, because only full randomization guarantees valid estimates of residual variance and unbiased estimates of effects. This argument, however, concerns the long-run properties of the procedure and seems of little help in this specific situation. Why should we care if the randomization yields correct estimates under replication of the experiment, if the particular experiment is jeopardized?

Another solution is to create a list of all possible allocations that we would accept and randomly choose one of these allocations for our experiment. The analysis should then reflect this restriction in the possible randomizations, which often renders this approach difficult to implement.

The most pragmatic method is to reject highly undesirable designs and compute a new randomization ( Cox 1958 ) . Undesirable allocations are unlikely to arise for large sample sizes, and we might accept a small bias in estimation for small sample sizes, when uncertainty in the estimated treatment effect is already high. In this approach, whenever we reject a particular outcome, we must also be willing to reject the outcome if we permute the treatment level labels. If we reject eight big and two small mice for kit A, then we must also reject two big and eight small mice. We must also be transparent and report a rejected allocation, so that critics may come to their own conclusions about potential biases and their remedies.

1.5.2 Blinding

Bias in treatment comparisons is also introduced if treatment allocation is random, but responses cannot be measured entirely objectively, or if knowledge of the assigned treatment affects the response. In clinical trials, for example, patients might react differently when they know to be on a placebo treatment, an effect known as cognitive bias . In animal experiments, caretakers might report more abnormal behavior for animals on a more severe treatment. Cognitive bias can be eliminated by concealing the treatment allocation from technicians or participants of a clinical trial, a technique called single-blinding .

If response measures are partially based on professional judgement (such as a clinical scale), patient or physician might unconsciously report lower scores for a placebo treatment, a phenomenon known as observer bias . Its removal requires double blinding , where treatment allocations are additionally concealed from the experimentalist.

Blinding requires randomized treatment allocation to begin with and substantial effort might be needed to implement it. Drug companies, for example, have to go to great lengths to ensure that a placebo looks, tastes, and feels similar enough to the actual drug. Additionally, blinding is often done by coding the treatment conditions and samples, and effect sizes and statistical significance are calculated before the code is revealed.

In clinical trials, double-blinding creates a conflict of interest. The attending physicians do not know which patient received which treatment, and thus accumulation of side-effects cannot be linked to any treatment. For this reason, clinical trials have a data monitoring committee not involved in the final analysis, that performs intermediate analyses of efficacy and safety at predefined intervals. If severe problems are detected, the committee might recommend altering or aborting the trial. The same might happen if one treatment already shows overwhelming evidence of superiority, such that it becomes unethical to withhold this treatment from the other patients.

1.5.3 Analysis Plan and Registration

An often overlooked source of bias has been termed the researcher degrees of freedom or garden of forking paths in the data analysis. For any set of data, there are many different options for its analysis: some results might be considered outliers and discarded, assumptions are made on error distributions and appropriate test statistics, different covariates might be included into a regression model. Often, multiple hypotheses are investigated and tested, and analyses are done separately on various (overlapping) subgroups. Hypotheses formed after looking at the data require additional care in their interpretation; almost never will \(p\) -values for these ad hoc or post hoc hypotheses be statistically justifiable. Many different measured response variables invite fishing expeditions , where patterns in the data are sought without an underlying hypothesis. Only reporting those sub-analyses that gave ‘interesting’ findings invariably leads to biased conclusions and is called cherry-picking or \(p\) -hacking (or much less flattering names).

The statistical analysis is always part of a larger scientific argument and we should consider the necessary computations in relation to building our scientific argument about the interpretation of the data. In addition to the statistical calculations, this interpretation requires substantial subject-matter knowledge and includes (many) non-statistical arguments. Two quotes highlight that experiment and analysis are a means to an end and not the end in itself.

There is a boundary in data interpretation beyond which formulas and quantitative decision procedures do not go, where judgment and style enter. ( Abelson 1995 )

Often, perfectly reasonable people come to perfectly reasonable decisions or conclusions based on nonstatistical evidence. Statistical analysis is a tool with which we support reasoning. It is not a goal in itself. ( Bailar III 1981 )

There is often a grey area between exploiting researcher degrees of freedom to arrive at a desired conclusion, and creative yet informed analyses of data. One way to navigate this area is to distinguish between exploratory studies and confirmatory studies . The former have no clearly stated scientific question, but are used to generate interesting hypotheses by identifying potential associations or effects that are then further investigated. Conclusions from these studies are very tentative and must be reported honestly as such. In contrast, standards are much higher for confirmatory studies, which investigate a specific predefined scientific question. Analysis plans and pre-registration of an experiment are accepted means for demonstrating lack of bias due to researcher degrees of freedom, and separating primary from secondary analyses allows emphasizing the main goals of the study.

Analysis Plan

The analysis plan is written before conducting the experiment and details the measurands and estimands, the hypotheses to be tested together with a power and sample size calculation, a discussion of relevant effect sizes, detection and handling of outliers and missing data, as well as steps for data normalization such as transformations and baseline corrections. If a regression model is required, its factors and covariates are outlined. Particularly in biology, handling measurements below the limit of quantification and saturation effects require careful consideration.

In the context of clinical trials, the problem of estimands has become a recent focus of attention. An estimand is the target of a statistical estimation procedure, for example the true average difference in enzyme levels between the two preparation kits. A main problem in many studies are post-randomization events that can change the estimand, even if the estimation procedure remains the same. For example, if kit B fails to produce usable samples for measurement in five out of ten cases because the enzyme level was too low, while kit A could handle these enzyme levels perfectly fine, then this might severely exaggerate the observed difference between the two kits. Similar problems arise in drug trials, when some patients stop taking one of the drugs due to side-effects or other complications.

Registration

Registration of experiments is an even more severe measure used in conjunction with an analysis plan and is becoming standard in clinical trials. Here, information about the trial, including the analysis plan, procedure to recruit patients, and stopping criteria, are registered in a public database. Publications based on the trial then refer to this registration, such that reviewers and readers can compare what the researchers intended to do and what they actually did. Similar portals for pre-clinical and translational research are also available.

1.6 Notes and Summary

The problem of measurements and measurands is further discussed for statistics in Hand ( 1996 ) and specifically for biological experiments in Coxon, Longstaff, and Burns ( 2019 ) . A general review of methods for handling missing data is Dong and Peng ( 2013 ) . The different roles of randomization are emphasized in Cox ( 2009 ) .

Two well-known reporting guidelines are the ARRIVE guidelines for animal research ( Kilkenny et al. 2010 ) and the CONSORT guidelines for clinical trials ( Moher et al. 2010 ) . Guidelines describing the minimal information required for reproducing experimental results have been developed for many types of experimental techniques, including microarrays (MIAME), RNA sequencing (MINSEQE), metabolomics (MSI) and proteomics (MIAPE) experiments; the FAIRSHARE initiative provides a more comprehensive collection ( Sansone et al. 2019 ) .

The problems of experimental design in animal experiments and particularly translation research are discussed in Couzin-Frankel ( 2013 ) . Multi-center studies are now considered for these investigations, and using a second laboratory already increases reproducibility substantially ( Richter et al. 2010 ; Richter 2017 ; Voelkl et al. 2018 ; Karp 2018 ) and allows standardizing the treatment effects ( Kafkafi et al. 2017 ) . First attempts are reported of using designs similar to clinical trials ( Llovera and Liesz 2016 ) . Exploratory-confirmatory research and external validity for animal studies is discussed in Kimmelman, Mogil, and Dirnagl ( 2014 ) and Pound and Ritskes-Hoitinga ( 2018 ) . Further information on pilot studies is found in Moore et al. ( 2011 ) , Sim ( 2019 ) , and Thabane et al. ( 2010 ) .

The deliberate use of statistical analyses and their interpretation for supporting a larger argument was called statistics as principled argument ( Abelson 1995 ) . Employing useless statistical analysis without reference to the actual scientific question is surrogate science ( Gigerenzer and Marewski 2014 ) and adaptive thinking is integral to meaningful statistical analysis ( Gigerenzer 2002 ) .

In an experiment, the investigator has full control over the experimental conditions applied to the experiment material. The experimental design gives the logical structure of an experiment: the units describing the organization of the experimental material, the treatments and their allocation to units, and the response. Statistical design of experiments includes techniques to ensure internal validity of an experiment, and methods to make inference from experimental data efficient.