linear modeling common core algebra ii homework answers

• Find your textbook
• Math Solver

• Big Ideas Math Algebra 2, Virginia Edition, 2019

• Big Ideas Math Algebra 2, 2014

• Big Ideas Math Algebra 2 Texas

• Big Ideas Math Algebra 2 A Bridge to Success

• Core Connections Algebra 2, 2013

• Houghton Mifflin Harcourt Algebra 2, 2015

• McGraw Hill Glencoe Algebra 2, 2012

• McGraw Hill Glencoe Algebra 2 Texas, 2016

• McGraw Hill Glencoe Algebra 2, 2017

• Pearson Algebra 2 Common Core, 2011

• Pearson Algebra 2 Common Core, 2013

Big Ideas Math Algebra 2 Answers Chapter 1 Linear Functions

For better preparation and good quality of education, we have shared the Big Ideas Math Algebra 2 Answers Chapter 1 Linear Functions for high school students. Provided BIM Math Book Algebra 2 Solution Key are aligned topic-wise as per the latest common core 2019 curriculum Big Ideas Math Textbook. So, students can easily understand the concepts of chapter 1 linear functions.

Linear functions topics are very hard to solve for high school students but it can be easy by practicing the questions covered in the Solution Key of Big Ideas Math Book Algebra 2 Chapter 1 Linear Functions . Also, you can download all topics BIM Algebra 2 Ch 1 Linear Functions Answer Key simply by clicking the available links below.

Big Ideas Math Book Algebra 2 Answer Key Chapter 1 Linear Functions

Step by Step Solutions explained for all the questions in the BIM Algebra 2 Ch 1 Solution key are easy to learn & understand as they are prepared by the professional subject experts. After referring to the topic wise Big Ideas Math Algebra 2 Answers Chapter 1 Linear Functions, every high school student can become a pro in the concepts and gain better subject knowledge. So, click on the respective links and start preparing each topic of the Big Ideas math book Algebra 2 Chapter 1 Linear Functions efficiently.

• Linear Functions Maintaining Mathematical Proficiency – Page 1
• Linear Functions Maintaining Mathematical Practices – Page 2
• Lesson 1.1 Parent Functions and Transformations – Page (4-10)
• Parent Functions and Transformations 1.1 Exercises – Page (8-10)
• Lesson 1.2 Transformations of Linear and Absolute Value Functions – Page (12-18)
• Transformations of Linear and Absolute Value Functions 1.2 Exercises – Page (16-18)
• Linear Functions Study Skills Taking Control of Your Class Time – Page 19
• Linear Functions 1.1-1.2 Quiz – Page 20
• Lesson 1.3 Modeling with Linear Functions – Page (22-28)
• Modeling with Linear Functions 1.3 Exercises – Page (26-28)
• Lesson 1.4 Solving Linear Systems – Page (30-36)
• Solving Linear Systems 1.4 Exercises – Page (34-36)
• Linear Functions Performance Task: Secret of the Hanging Baskets – Page 37
• Linear Functions Chapter Review – Page (38-40)
• Linear Functions Chapter Test – Page 41
• Linear Functions Cumulative Assessment – Page (42-43)

Linear Functions Maintaining Mathematical Proficiency

Question 1. 5 • 2 3 + 7 Answer: 5 • 2 3 + 7 5.8+7 40+7 47

Question 2. 4 – 2(3 + 2) 2

4 – 2(3 + 2) 2 4 – 2 (25) 4  – 2 (25) 4 – 50 = – 46

Question 3. 48 ÷ 4 2 + \(\frac{3}{5}\) Answer: 48 ÷ 4 2 + \(\frac{3}{5}\) 48 ÷ 16 + \(\frac{3}{5}\) 3 + \(\frac{3}{5}\) = 3.6

Question 4. 50 ÷ 5 2 • 2 Answer: 50 ÷ 5 2 • 2 50 ÷ 25 . 2 2 .2 4

Question 5. \(\frac{1}{2}\)(2 2 + 22) Answer: \(\frac{1}{2}\)(2 2 + 22) \(\frac{1}{2}\)(4+ 22) \(\frac{1}{2}\)(26) = 13

Question 6. \(\frac{1}{6}\)(6 + 18) – 2 2

Answer: \(\frac{1}{6}\)(6 + 18) – 2 2 \(\frac{1}{6}\)(24) – 4 4 – 4 = 0

Graph the transformation of the figure.

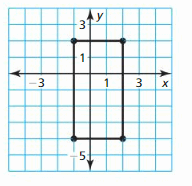
Question 10. ABSTRACT REASONING Give an example to show why the order of operations is important when evaluating a numerical expression. Is the order of transformations of figures important? Justify your answer. Answer: The  order of operations  tells us the  order  to solve steps in  expressions  with more than one  operation . First, we solve any  operations inside of parentheses or brackets.

Linear Functions Maintaining Mathematical Practices

Monitoring Progress

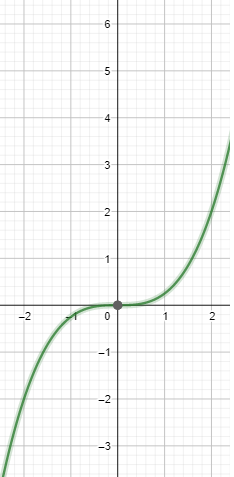
Use a graphing calculator to graph the equation using the standard viewing window and a square viewing window. Describe any differences in the graphs.

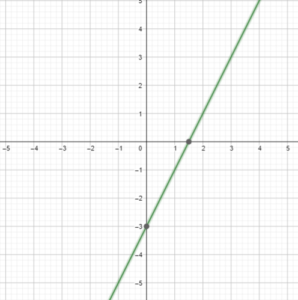
Question 6. y = 0.25x 3

Determine whether the viewing window is square. Explain.

Question 7. -8 ≤ x ≤ 8, -2 ≤ y ≤ 8 Answer: -8 ≤ x ≤ 8, -2 ≤ y ≤ 8 The total range of X-axis is 16 units and the total range of Y-axis is 10 units The ratio of the height to width of the viewing screen is 10/16 = 5/8 So, the ratio is 5:8. Thus the viewing window is square.

Question 8. -7 ≤ x ≤ 8, -2 ≤ y ≤ 8 Answer: -7 ≤ x ≤ 8, -2 ≤ y ≤ 8 The total range of X-axis is 15 units and the total range of Y-axis is 10 units The ratio of the height to width of the viewing screen is 10/15 = 2/3 So, the ratio is 2:3. Thus the viewing window is square.

Question 9. -6 ≤ x ≤ 9, -2 ≤ y ≤ 8 Answer: -6 ≤ x ≤ 9, -2 ≤ y ≤ 8 The total range of X-axis is 15 units and the total range of Y-axis is 10 units The ratio of the height to width of the viewing screen is 10/15 = 2/3 So, the ratio is 2:3. Thus the viewing window is square.

Question 10. -2 ≤ x≤ 2, -3 ≤ y ≤ 3 Answer: -2 ≤ x≤ 2, -3 ≤ y ≤ 3 The total range of X-axis is 4 units and the total range of Y-axis is 6 units The ratio of the height to width of the viewing screen is 6/4 = 3/2 So, the ratio is 3:2. Thus the viewing window is not a square.

Question 11. -4 ≤ x ≤ 5, -3 ≤ y ≤ 3 Answer: -4 ≤ x ≤ 5, -3 ≤ y ≤ 3 The total range of X-axis is 9 units and the total range of Y-axis is 6 units The ratio of the height to width of the viewing screen is 6/9 = 2/3 So, the ratio is 2:3. Thus the viewing window is a square.

Question 12. -4 ≤ x ≤ 4, -3 ≤ y ≤ 3 Answer: -4 ≤ x ≤ 4, -3 ≤ y ≤ 3 The total range of X-axis is 8 units and the total range of Y-axis is 6 units The ratio of the height to width of the viewing screen is 6/8 = 2/3 So, the ratio is 2:3. Thus the viewing window is a square.

Lesson 1.1 Parent Functions and Transformations

Essential Question

What are the characteristics of some of the basic parent functions?

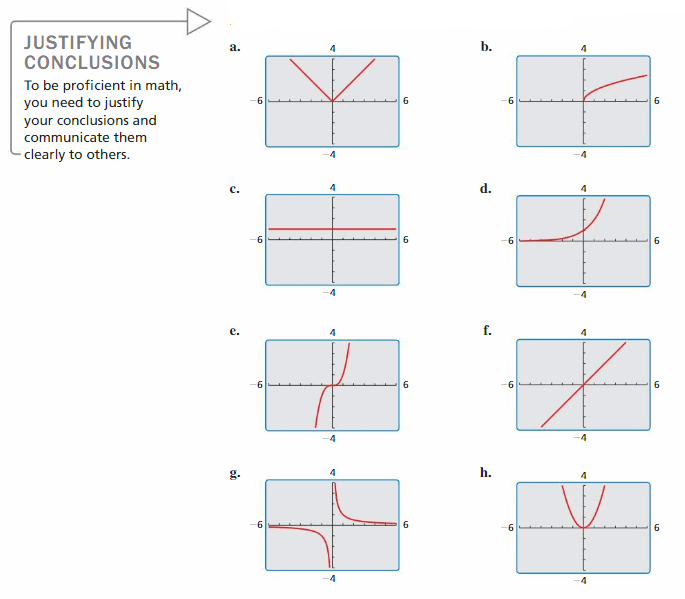
Communicate Your Answer

Question 2. What are the characteristics of some of the basic parent functions? Answer: Key common points of linear parent functions include the fact that the: Equation is y = x. Domain and  range  are real numbers. Slope, or rate of change, is constant.

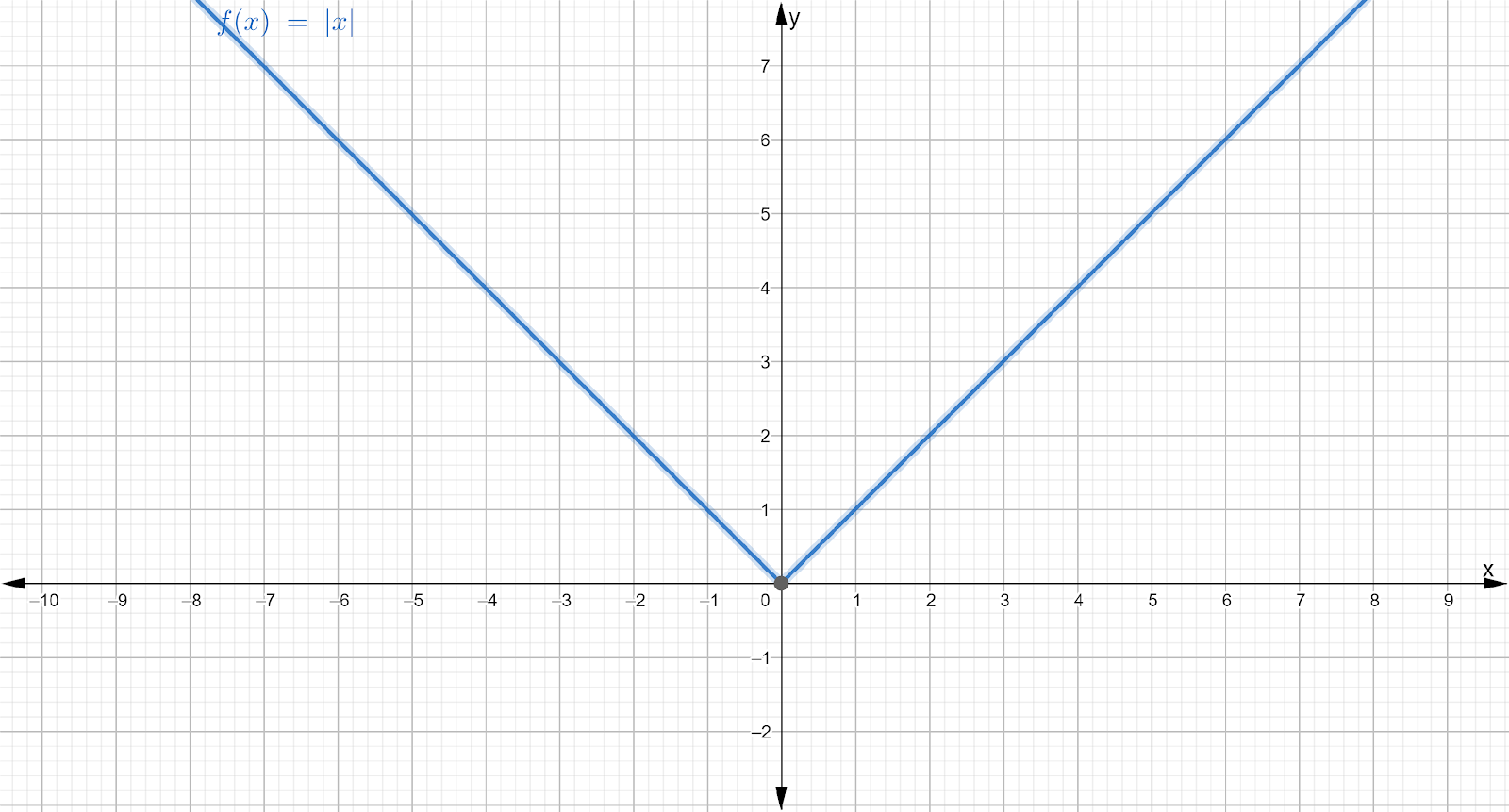
Graph the function and its parent function. Then describe the transformation.

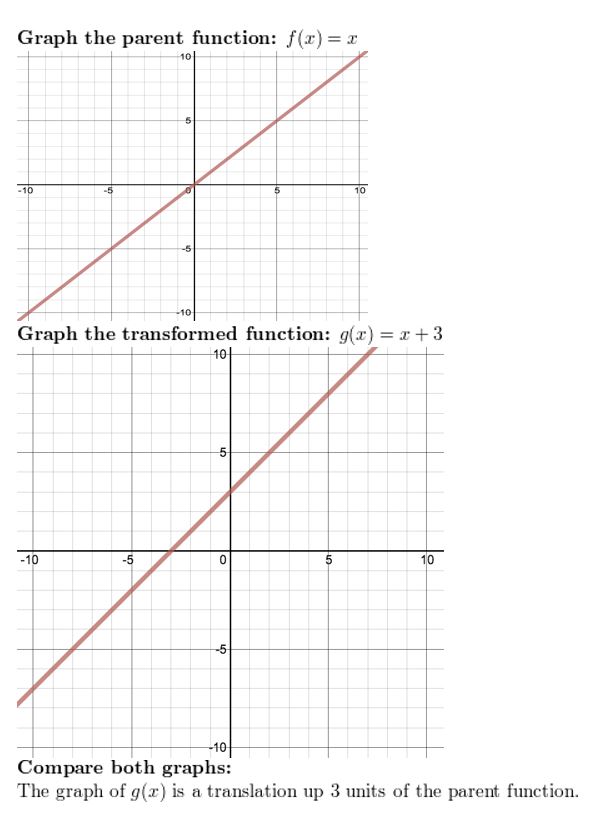
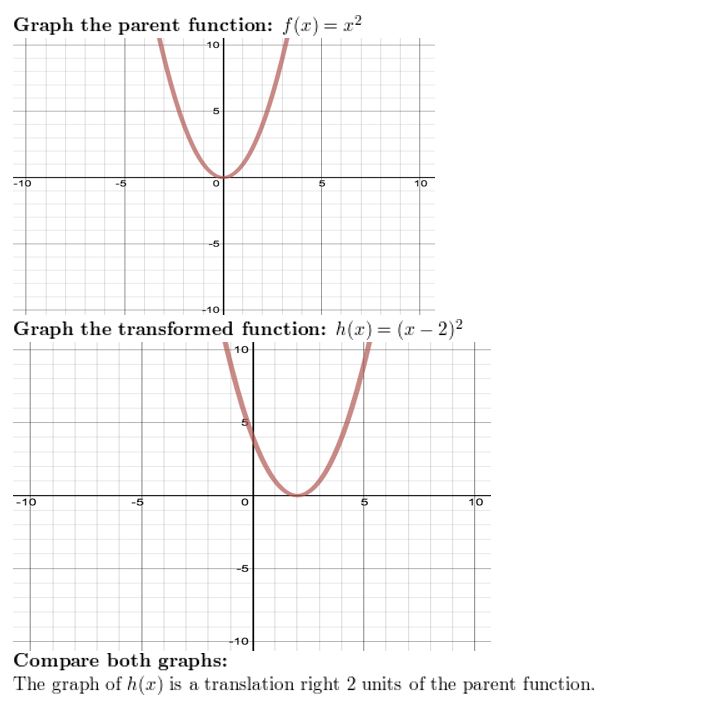
Question 3. h(x) = (x – 2) 2

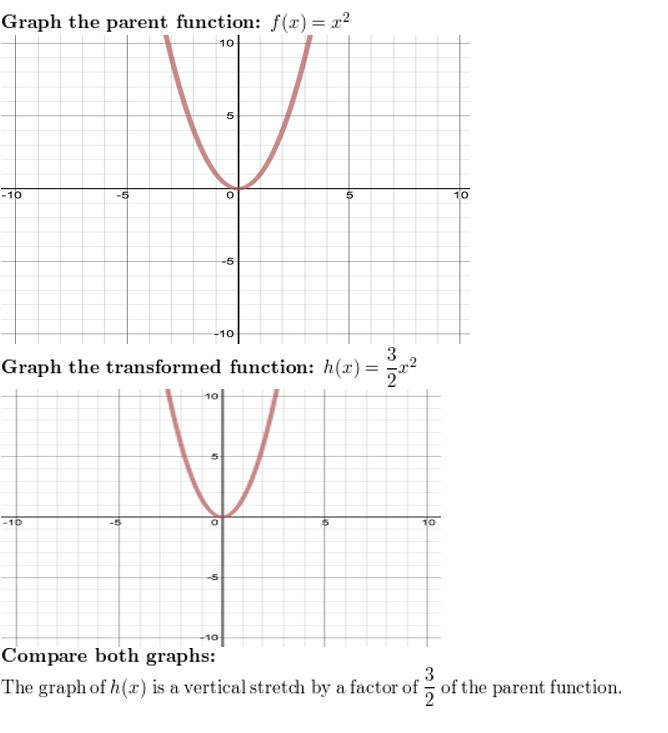
Question 6. h(x) = \(\frac{3}{2}\)x 2

Use a graphing calculator to graph the function and its parent function. Then describe the transformations

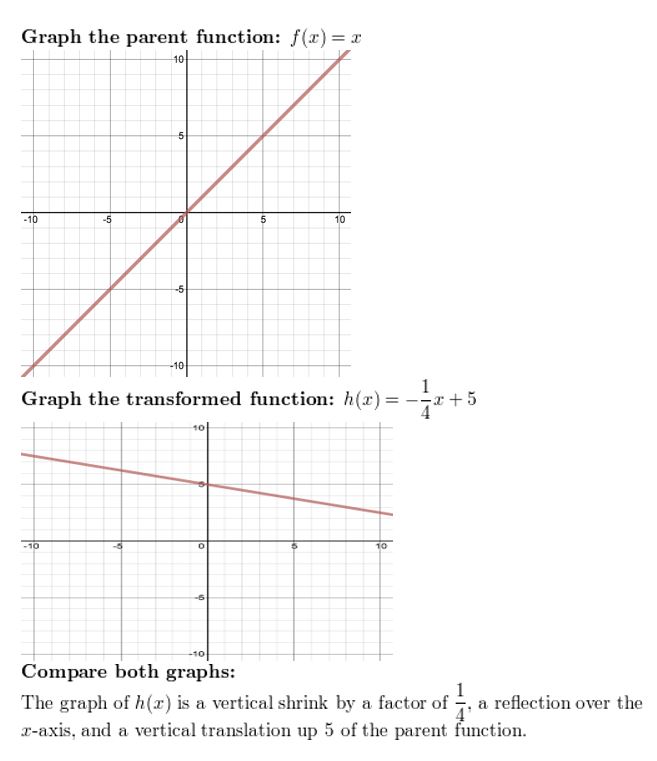
Parent Functions and Transformations 1.1 Exercises

Vocabulary and Core Concept Check

Monitoring Progress and Modeling with Mathematics

In Exercises 3–6, identify the function family to which f belongs. Compare the graph of f to the graph of its parent function.

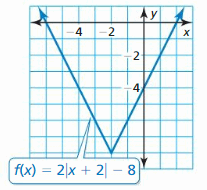
In Exercises 9–18, graph the function and its parent function. Then describe the transformation.

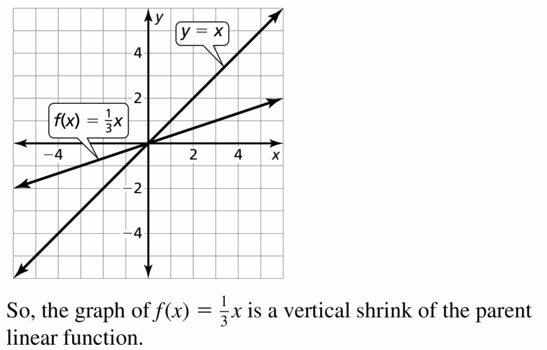
In Exercises 19–26, graph the function and its parent function. Then describe the transformation.

In Exercises 27–34, use a graphing calculator to graph the function and its parent function. Then describe the transformations.

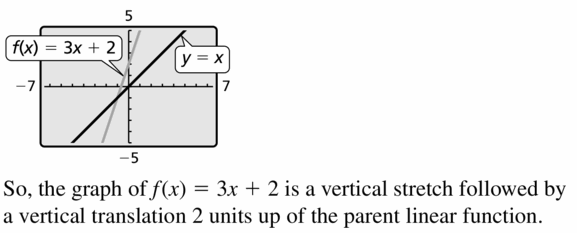
ERROR ANALYSIS In Exercises 35 and 36, identify and correct the error in describing the transformation of the parent function.

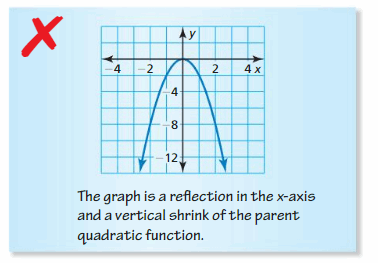
MATHEMATICAL CONNECTIONS In Exercises 37 and 38, find the coordinates of the figure after the transformation.

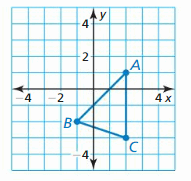
USING TOOLS In Exercises 39–44, identify the function family and describe the domain and range. Use a graphing calculator to verify your answer.

Maintaining Mathematical Proficiency

Determine whether the ordered pair is a solution of the equation. (Skills Review Handbook)

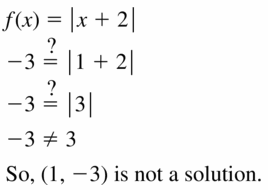
Find the x-intercept and the y-intercept of the graph of the equation. (Skills Review Handbook)

Question 60. y = x + 2 Answer: To find the x-intercept let y = 0, the solve for x. y = x + 2 0 = x + 2 x = -2 To find the y-intercept let x = 0, then solve for y. y = x+ 2 y = 0 + 2 y = 2 So, the intercept is (0, 0) and the y-intercept is (-2, 2)

Lesson 1.2 Transformations of Linear and Absolute Value Functions

How do the graphs of y = f(x) + k, y = f(x – h), and y = -f(x) compare to the graph of the parent function f?

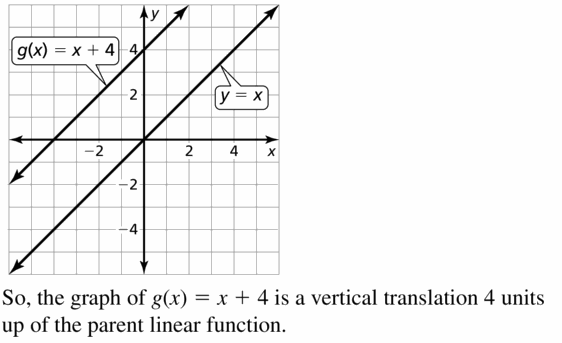
Question 4. Transformation How do the graphs of y = f (x) + k, y = f(x – h), and y = -f(x) compare to the graph of the parent function f? Answer: The graphs of y = f (x) + k, y = f(x – h), and y = -f(x) are compared to the graph of the parent function by vertical shifts, horizontal shifts and reflections.

• Vertical shifts: Let f(x) be the parent function and k be a positive number. To graph the function y = f (x) + k, we shift the graph of y = f(x) up k units by adding k to the y-coordinates of the points on the graph of f.
• Horizontal shifts: Let f(x) be the parent function and h be a positive number. To graph the function y = f(x – h), we shift the graph of y = f(x) to the right h units by adding h to the x-coordinates of the points on the graph of f.
• Reflections: Let f(x) be the parent function. To graph the function y = -f(x), we reflect the graph of y = f(x) about the x-axis by multiplying the y-coordinates of the points on the graph of f by -1.

Question 5. Compare the graph of each function to the graph of its parent function f. Use a graphing calculator to verify your answers are correct. a. y = \([\sqrt{x}/latex] – 4 b. y = [latex][\sqrt{x + 4}/latex] c. y = –[latex][\sqrt{x}/latex] d. y = x 2 + 1 e. y = (x – 1) 2 f. y = -x 2

Write a function g whose graph represents the indicated transformation of the graph of f. Use a graphing calculator to check your answer.

Transformations of Linear and Absolute Value Functions 1.2 Exercises

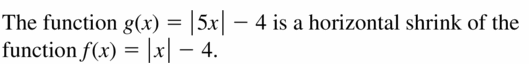
In Exercises 3–8, write a function g whose graph represents the indicated transformation of the graph of f. Use a graphing calculator to check your answer.

In Exercises 11–16, write a function g whose graph represents the indicated transformation of the graph of f. Use a graphing calculator to check your answer.

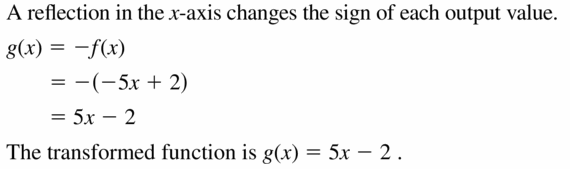
In Exercises 17–22, write a function g whose graph represents the indicated transformation of the graph of f. Use a graphing calculator to check your answer.

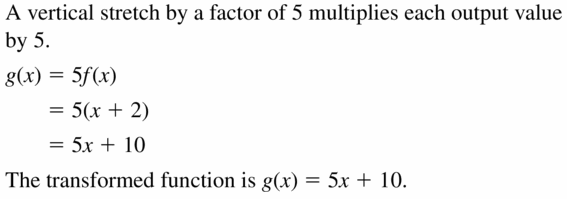
In Exercises 27–32, write a function g whose graph represents the indicated transformations of the graph of f.

ERROR ANALYSIS In Exercises 33 and 34, identify and correct the error in writing the function g whose graph represents the indicated transformations of the graph of f.

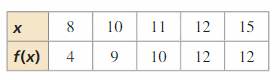
MATHEMATICAL CONNECTIONS For Exercises 37–40, describe the transformation of the graph of f to the graph of g. Then find the area of the shaded triangle.

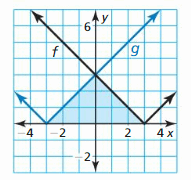
Evaluate the function for the given value of x. (Skills Review Handbook)

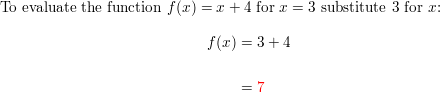
Create a scatter plot of the data. (Skills Review Handbook)

Linear Functions Study Skills Taking Control of Your Class Time

1.1 – 1.2 What Did You Learn?

Core Concepts

Mathematical Practices

Question 1. How can you analyze the values given in the table in Exercise 45 on page 9 to help you determine what type of function models the data?

Question 2. Explain how you would round your answer in Exercise 10 on page 16 if the extra expense is $13,500.

Study Skills

Taking Control of Your Class Time

Question 1. Sit where you can easily see and hear the teacher, and the teacher can see you.

Question 2. Pay attention to what the teacher says about math, not just what is written on the board.

Question 3. Ask a question if the teacher is moving through the material too fast.

Question 4. Try to memorize new information while learning it.

Question 5. Ask for clarification if you do not understand something.

Question 6. Think as intensely as if you were going to take a quiz on the material at the end of class.

Question 7. Volunteer when the teacher asks for someone to go up to the board.

Question 8. At the end of class, identify concepts or problems for which you still need clarification.

Question 9. Use the tutorials at BigIdeasMath.com for additional help.

Linear Functions 1.1-1.2 Quiz

Identify the function family to which g belongs. Compare the graph of the function to the graph of its parent function. (Section 1.1)

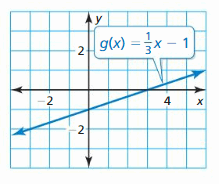
Graph the function and its parent function. Then describe the transformation. (Section 1.1)

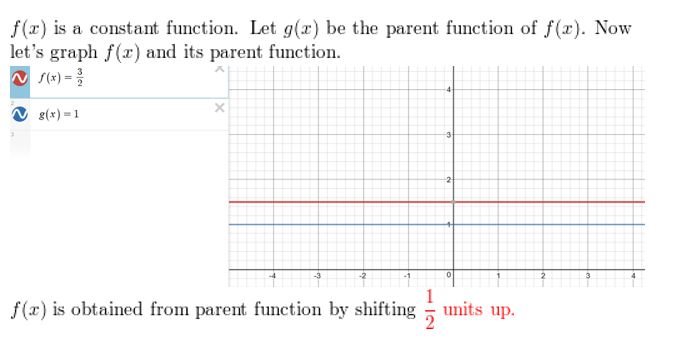
Question 6. f(x) = 2(x – 1) 2

Write a function g whose graph represents the indicated transformation of the graph of f. (Section 1.2)

Question 10. f(x) = 2x + 1; translation 3 units up Answer: The vertex is (0, 1) of the original graph to move the vertex up by 3 units just add 3 to the y-intercept. g(x) = 2x + 4

Question 11. f(x) = -3 | x – 4 | ; vertical shrink by a factor of \(\frac{1}{2}\) Answer: f(x) = -3 | x – 4 | to vertically shrink a function by a factor by c, multiply the whole function by c f(x) vertically shrunk by a factor of c would be cf(x) so f(x) = -3 | x – 4 | vertically shrunk by a factor of 1/2 would be f(x) = (-3/2) |x – 4|

Question 12. f(x) = 3 | x + 5 |; reflection in the x-axis Answer: f(x) = 3 | x + 5 | The points reflected in the x-axis have opposite y-coordinates f(x) = -y -y = -3 |x + 5| f(x) = -3 |x + 5|

Question 13. f(x) = \(\frac{1}{3}\)x – \(\frac{2}{3}\) ; translation 4 units left Answer: f(x) = \(\frac{1}{3}\)x – \(\frac{2}{3}\) f(x) = \(\frac{1}{3}\) (x – 2) f(x) = \(\frac{1}{3}\) (x – 2 + 4) f(x) = \(\frac{1}{3}\) (x + 2) f(x) = \(\frac{1}{3}\)x + \(\frac{2}{3}\)

Write a function g whose graph represents the indicated transformations of the graph of f. (Section 1.2)

Question 14. Let g be a translation 2 units down and a horizontal shrink by a factor of \(\frac{2}{3}\) of the graph of f(x) =x. Answer: f(x) =x horizontal shrink by a factor of \(\frac{2}{3}\) f(x) = \(\frac{3}{2}\)x f(x) = \(\frac{3}{2}\)x – 2 g(x) =\(\frac{3}{2}\)x – 2

Question 15. Let g be a translation 9 units down followed by a reflection in the y-axis of the graph of f(x) = x. Answer: f(x) =x g(x) = f(x) – 9 It is also reflected about the y-axis. g(x) = f(-x) – 9

Question 16. Let g be a reflection in the x-axis and a vertical stretch by a factor of 4 followed by a translation 7 units down and 1 unit right of the graph of f(x) = | x |. Answer: f(x) = |x| g(x) = bf(x) Reflecting function over the x-axis g(x) = -f(x) Original function is f(x) = -|x| Stretching by a factor of 4 means we have to multiply by 4. g(x) = -4|x| g(x) = -4x translation 7 units down and 1 unit right of the graph of f(x) = | x | g(x) = -4x – 7 -1 g(x) = -4x – 8 g(x) = -4(x + 2)

Question 17. Let g be a translation 1 unit down and 2 units left followed by a vertical shrink by a factor of \(\frac{1}{2}\) of the graph of f(x) = | x |. Answer: f(x) = |x| Multiply output with 1/2 to vertically shrink function g(x) = 1/2 |x| Subtract 1 to output of function to translate 1 unit down and 2 units left. g(x) = 1/2 |x| – 1 -2 g(x) = 1/2 |x| – 3

Question 19. The total cost of an annual pass plus camping for x days in a National Park can be modeled by the function f(x) = 20x+ 80. Senior citizens pay half of this price and receive an additional $30 discount. Describe how to transform the graph of f to model the total cost for a senior citizen. What is the total cost for a senior citizen to go camping for three days? (Section 1.2) Answer: Total cost of annual pass plus camping for x days f(x) = 2x + 80 For senior citizen cost = 1/2 (20x + 80) – 30 = 10x + 40 – 30 = 10x + 10 = 10(x + 1) x = 3 = 10(3 + 1) = 10(4) = $40

Lesson 1.3 Modeling with Linear Functions

Essential Question How can you use a linear function to model and analyze a real-life situation?

Question 3. How can you use a linear function to model and analyze a real-life situation? Answer: One of the real life situation is finding Variable costs. Imagine that you are taking a taxi while on vacation. You know that the taxi service charges 9 rupees to pick your family up from your hotel and another 0.15 rupees per mile for the trip. Without knowing how many miles it will be to each destination, you can set up a linear equation that can be used to find the cost of any taxi trip you take on your trip. By using′ ′x′′ to represent the number of miles to your destination and ”y′′ to represent the cost of that taxi ride, the linear equation would be: y = 0.15x+9 For Example: If one company offers to pay you 450 rupees per week and the other offers 10 rupees per hour, and both ask you to work 40 hours per week, which company is offering the better rate of pay? A linear equation can help you figure it out. The first company’s offer is expressed as 450 = 40x. The second company’s offer is expressed as y = 10. After comparing the two offers, the equations tell you the first company is offering a better rate of pay at 11.25 rupees per hour.

Question 4. Use the Internet or some other reference to find a real-life example of straight line depreciation. a. Use a spreadsheet to show the depreciation. b. Write a function that models the depreciation. c. Sketch a graph of the function.

Answer: The real life example of straight line depreciation is the decrease of speed of car by ten meter per second which was moving with an initial speed of a hundred meter per second till speed reaches thirty meter per second.

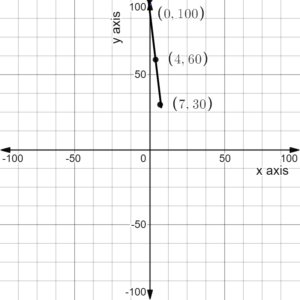
Modeling with Linear Functions 1.3 Exercises

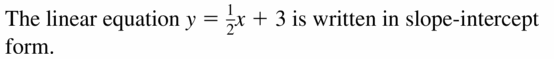
In Exercises 3–8, use the graph to write an equation of the line and interpret the slope.

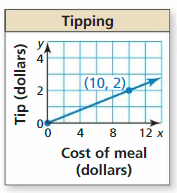
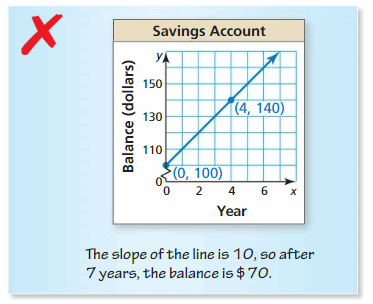
ERROR ANALYSIS In Exercises 11 and 12, describe and correct the error in interpreting the slope in the context of the situation.

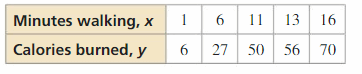
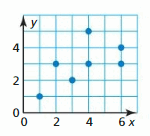
In Exercises 13–16, determine whether the data show a linear relationship. If so, write an equation of a line of fit. Estimate y when x = 15 and explain its meaning in the context of the situation.

USING TOOLS In Exercises 19–24, use the linear regression feature on a graphing calculator to find an equation of the line of best fit for the data. Find and interpret the correlation coefficient.

b. What is the domain and range of the function? What does each represent? Answer: Because x and y are linear function, and k = -5/4, (0, 30) is on the function. y = -5/4 x + 30 And the domain is [0, 24] and the range is [0, 30] and the range represents the total money still to be paid.

c. How much do you still owe after making payments for 12 months? Answer: Because y = -5/4 x + 30 when x = 12, y = 15 So, you still owe 15 hundreds of dollars.

Solve the system of linear equations in two variables by elimination or substitution. (Skills Review Handbook)

Lesson 1.4 Solving Linear Systems

Essential Question How can you determine the number of solutions of a linear system? A linear system is consistent when it has at least one solution. A linear system is inconsistent when it has no solution.

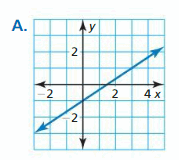
Answer: 2x – 3y = 3 —- × 2 ⇒ 4x – 6y = 6 -4x + 6y = 6

4x – 6y = 6 -4x + 6y = 6 0 So, the linear system is inconsistent.

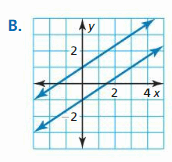
Answer: 2x – 3y = 3 x + 2y = 5 —– × 2 2x + 4y = 10

2x – 3y = 3 (-)2x + 4y = 10 -7y = -7 y = 1 x + 2 = 5 x = 3 So, x = 3 and y = 1 So, the system is consistent

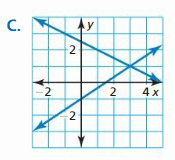
Answer: 2x – 3y = 3 —- × 2 -4x + 6y = 6

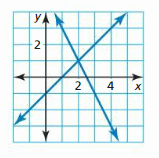
Answer: x + y = 0  — × 2 = 2x + 2y = 0 3x + 2y = 1

2x + 2y = 0 (-)3x + 2y = 1 -x = -1 x = 1 The linear system has one solution

Question 3. How can you determine the number of solutions of a linear system? Answer: A linear equation in two variables is an equation of the form ax + by + c = 0 where a, b, c ∈ R, a, and b ≠ 0. When we consider a system of linear equations, we can find the number of solutions by comparing the coefficients of the variables of the equations.

• Solve one equation for one of its variables.
• Substitute the expression from point 1 in the other two equations to obtain a linear system in two variables.
• Solve the new linear system for both of its variables.
• Substitute the values found in point 3 into one of the original equations and solve for the remaining variable.

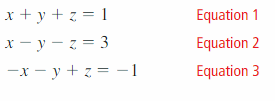
Solving Linear Systems 1.4 Exercises

In Exercises 3–8, solve the system using the elimination method.

Question 4. x + 4y – 6z = -1 2x – y + 2z = -7 -x + 2y – 4z = 5 Answer: x + 4y – 6z = -1— (1) 2x – y + 2z = -7 —- (2) -x + 2y – 4z = 5 —-(3) Solving 1 & 3 x + 4y – 6z = -1 -x + 2y – 4z = 5 6y – 10z = 4 3y – 5z = 2 — (4) Solving (1) & (2) x + 4y – 6z = -1 — × 2 ⇒ 2x + 6y – 12z = -2 2x – y + 2z = -7

2x + 6y – 12z = -2 2x – y + 2z = -7 –    +    –        + 7y – 14z = 5 —- (5) Solving (2) & (3) 2x – y + 2z = -7 —- (2) -x + 2y – 4z = 5 —-(3)—–×2 ⇒ -2x + 4y – 8z = 10

2x – y + 2z = -7 -2x + 4y – 8z = 10 3y – 5z = 3 — (6) Solving 5 & 6 7y – 14z = 5 — × 3 ⇒ 21y – 42z = 15 — (7) 3y – 5z = 3 — × 7 ⇒ 21y – 35z = 21 — (8)

21y – 42z = 15 21y – 35z = 21 -7z = -6 z = 6/7 or 0.85 7y – 14z = 5 7y – 14(6/7) = 5 7y – 14(6) = 5 7y – 84 = 5 7y = 5 + 84 7y = 89 y = 89/7 y = 12.7

-x + 2y – 4z = 5 -x + 2(12.7) – 4(0.85) = 5 -x + 25.4 – 3.4 = 5 -x + 22 = 5 -x = 5 – 22 -x = -17 x = 17 The solution is (17, 12.7, 0.85)

Question 6. 3x + 2y – z = 8 -3x + 4y + 5z = -14 x – 3y + 4z = -14

ERROR ANALYSIS In Exercises 9 and 10, describe and correct the error in the first step of solving the system of linear equations.

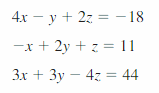
In Exercises 11–16, solve the system using the elimination method.

In Exercises 19–28, solve the system of linear equations using the substitution method.

MATHEMATICAL CONNECTIONS In Exercises 33 and 34, write and use a linear system to answer the question.

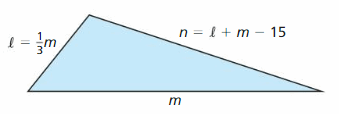
Simplify. (Skills Review Handbook)

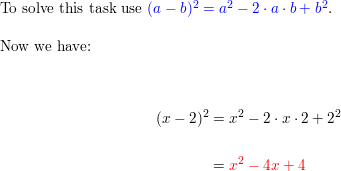
Write a function g described by the given transformation of f(x) =∣x∣− 5 .(Section 1.2)

Linear Functions Performance Task: Secret of the Hanging Baskets

1.3–1.4 What Did You Learn?

Core Concepts Section 1.3 Writing an Equation of a Line, p. 22 Finding a Line of Fit, p. 24 Section 1.4 Solving a Three-Variable System, p. 31 Solving Real-Life Problems, p. 33

Question 1. Describe how you can write the equation of the line in Exercise 7 on page 26 using only one of the labeled points.

Question 2. How did you use the information in the newspaper article in Exercise 30 on page 35 to write a system of three linear equations?

Question 3. Explain the strategy you used to choose the values for a, b, and c in Exercise 35 part (a) on page 35.

Performance Task

Linear Functions Chapter Review

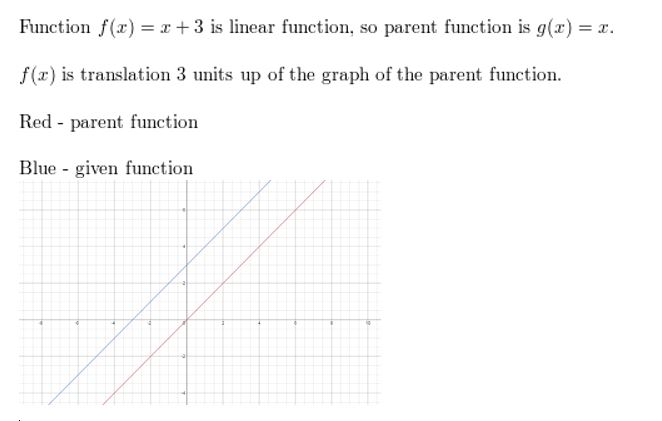
Question 3. h(x) = \(\frac{1}{2}\)x 2

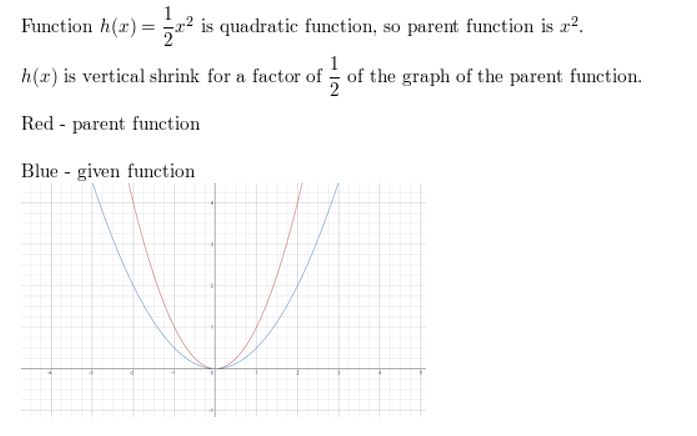
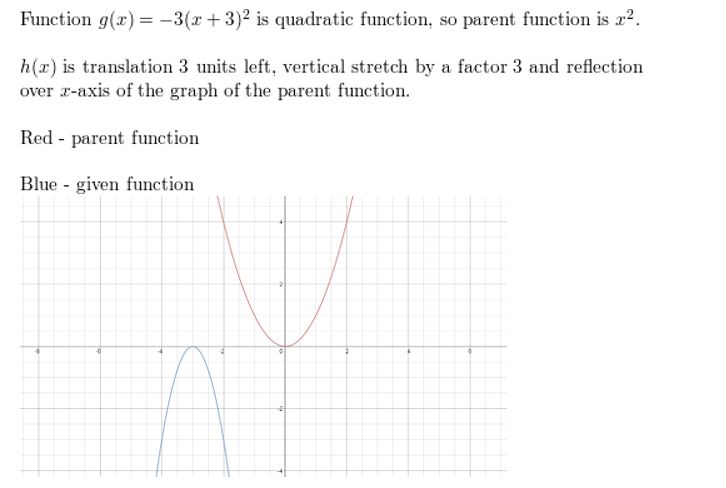
Question 6. g(x) = -3(x + 3) 2

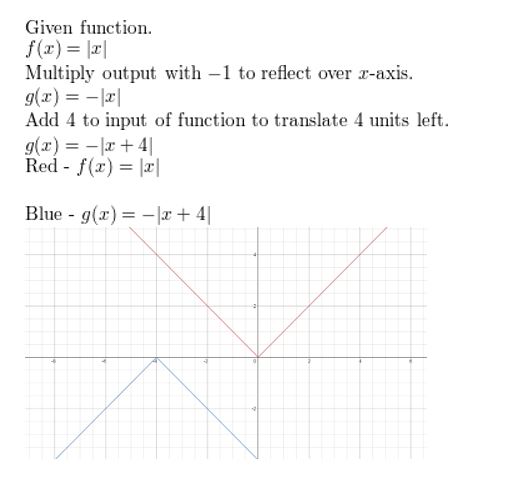
Write a function g whose graph represents the indicated transformations of the graph of f. Use a graphing calculator to check your answer.

Question 11. You ride your bike and measure how far you travel. After 10 minutes, you travel 3.5 miles. After 30 minutes, you travel 10.5 miles. Write an equation to model your distance. How far can you ride your bike in 45 minutes? Answer: Given, You ride your bike and measure how far you travel. After 10 minutes, you travel 3.5 miles. After 30 minutes, you travel 10.5 miles. m = (10.5 – 3.5)/30 – 10 m = 7/20 y – 3.5 = 7/20(x – 10) y – 3.5 = 7/20 x – 3.5 y = 7/20x x = 45 y = 7/20 (45) y = 15.75 miles

Linear Functions Chapter Test

Write an equation of the line and interpret the slope and y-intercept.

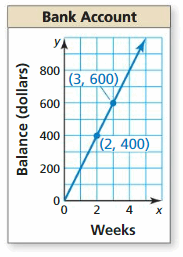
Solve the system. Check your solution, if possible.

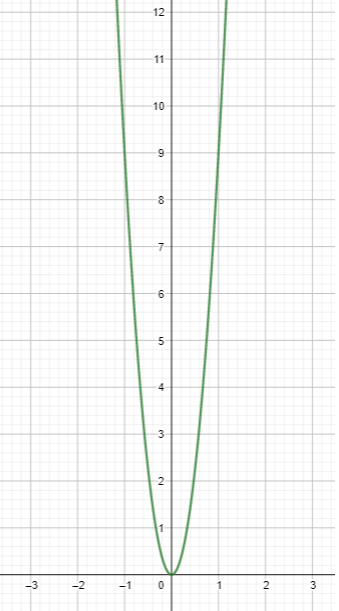
Question 7. f(x) = (3x) 2

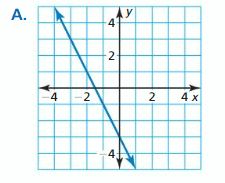
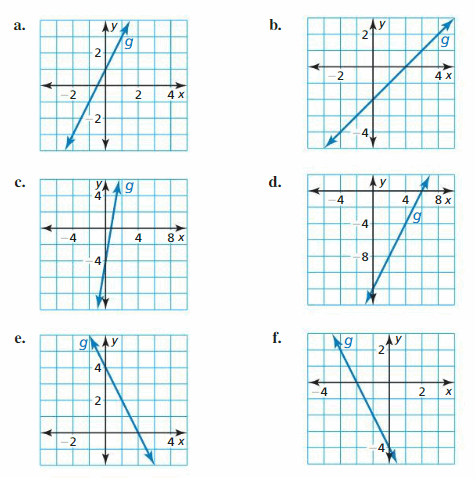
Match the transformation of f(x) = x with its graph. Then write a rule for g.

Linear Functions Cumulative Assessment

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.