two tailed hypothesis test calculator

t-test Calculator

Table of contents

Welcome to our t-test calculator! Here you can not only easily perform one-sample t-tests , but also two-sample t-tests , as well as paired t-tests .

Do you prefer to find the p-value from t-test, or would you rather find the t-test critical values? Well, this t-test calculator can do both! 😊

What does a t-test tell you? Take a look at the text below, where we explain what actually gets tested when various types of t-tests are performed. Also, we explain when to use t-tests (in particular, whether to use the z-test vs. t-test) and what assumptions your data should satisfy for the results of a t-test to be valid. If you've ever wanted to know how to do a t-test by hand, we provide the necessary t-test formula, as well as tell you how to determine the number of degrees of freedom in a t-test.

When to use a t-test?

A t-test is one of the most popular statistical tests for location , i.e., it deals with the population(s) mean value(s).

There are different types of t-tests that you can perform:

• A one-sample t-test;
• A two-sample t-test; and
• A paired t-test.

In the next section , we explain when to use which. Remember that a t-test can only be used for one or two groups . If you need to compare three (or more) means, use the analysis of variance ( ANOVA ) method.

The t-test is a parametric test, meaning that your data has to fulfill some assumptions :

• The data points are independent; AND
• The data, at least approximately, follow a normal distribution .

If your sample doesn't fit these assumptions, you can resort to nonparametric alternatives. Visit our Mann–Whitney U test calculator or the Wilcoxon rank-sum test calculator to learn more. Other possibilities include the Wilcoxon signed-rank test or the sign test.

Which t-test?

Your choice of t-test depends on whether you are studying one group or two groups:

One sample t-test

Choose the one-sample t-test to check if the mean of a population is equal to some pre-set hypothesized value .

The average volume of a drink sold in 0.33 l cans — is it really equal to 330 ml?

The average weight of people from a specific city — is it different from the national average?

Two-sample t-test

Choose the two-sample t-test to check if the difference between the means of two populations is equal to some pre-determined value when the two samples have been chosen independently of each other.

In particular, you can use this test to check whether the two groups are different from one another .

The average difference in weight gain in two groups of people: one group was on a high-carb diet and the other on a high-fat diet.

The average difference in the results of a math test from students at two different universities.

This test is sometimes referred to as an independent samples t-test , or an unpaired samples t-test .

Paired t-test

A paired t-test is used to investigate the change in the mean of a population before and after some experimental intervention , based on a paired sample, i.e., when each subject has been measured twice: before and after treatment.

In particular, you can use this test to check whether, on average, the treatment has had any effect on the population .

The change in student test performance before and after taking a course.

The change in blood pressure in patients before and after administering some drug.

How to do a t-test?

So, you've decided which t-test to perform. These next steps will tell you how to calculate the p-value from t-test or its critical values, and then which decision to make about the null hypothesis.

Decide on the alternative hypothesis :

Use a two-tailed t-test if you only care whether the population's mean (or, in the case of two populations, the difference between the populations' means) agrees or disagrees with the pre-set value.

Use a one-tailed t-test if you want to test whether this mean (or difference in means) is greater/less than the pre-set value.

Compute your T-score value :

Formulas for the test statistic in t-tests include the sample size , as well as its mean and standard deviation . The exact formula depends on the t-test type — check the sections dedicated to each particular test for more details.

Determine the degrees of freedom for the t-test:

The degrees of freedom are the number of observations in a sample that are free to vary as we estimate statistical parameters. In the simplest case, the number of degrees of freedom equals your sample size minus the number of parameters you need to estimate . Again, the exact formula depends on the t-test you want to perform — check the sections below for details.

The degrees of freedom are essential, as they determine the distribution followed by your T-score (under the null hypothesis). If there are d degrees of freedom, then the distribution of the test statistics is the t-Student distribution with d degrees of freedom . This distribution has a shape similar to N(0,1) (bell-shaped and symmetric) but has heavier tails . If the number of degrees of freedom is large (>30), which generically happens for large samples, the t-Student distribution is practically indistinguishable from N(0,1).

💡 The t-Student distribution owes its name to William Sealy Gosset, who, in 1908, published his paper on the t-test under the pseudonym "Student". Gosset worked at the famous Guinness Brewery in Dublin, Ireland, and devised the t-test as an economical way to monitor the quality of beer. Cheers! 🍺🍺🍺

p-value from t-test

Recall that the p-value is the probability (calculated under the assumption that the null hypothesis is true) that the test statistic will produce values at least as extreme as the T-score produced for your sample . As probabilities correspond to areas under the density function, p-value from t-test can be nicely illustrated with the help of the following pictures:

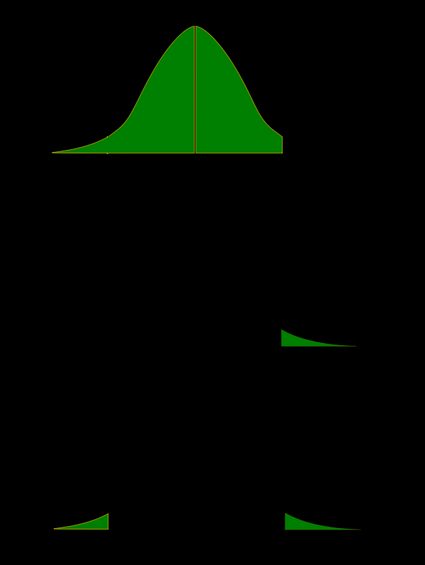
The following formulae say how to calculate p-value from t-test. By cdf t,d we denote the cumulative distribution function of the t-Student distribution with d degrees of freedom:

p-value from left-tailed t-test:

p-value = cdf t,d (t score )

p-value from right-tailed t-test:

p-value = 1 − cdf t,d (t score )

p-value from two-tailed t-test:

p-value = 2 × cdf t,d (−|t score |)

or, equivalently: p-value = 2 − 2 × cdf t,d (|t score |)

However, the cdf of the t-distribution is given by a somewhat complicated formula. To find the p-value by hand, you would need to resort to statistical tables, where approximate cdf values are collected, or to specialized statistical software. Fortunately, our t-test calculator determines the p-value from t-test for you in the blink of an eye!

t-test critical values

Recall, that in the critical values approach to hypothesis testing, you need to set a significance level, α, before computing the critical values , which in turn give rise to critical regions (a.k.a. rejection regions).

Formulas for critical values employ the quantile function of t-distribution, i.e., the inverse of the cdf :

Critical value for left-tailed t-test: cdf t,d -1 (α)

critical region:

(-∞, cdf t,d -1 (α)]

Critical value for right-tailed t-test: cdf t,d -1 (1-α)

[cdf t,d -1 (1-α), ∞)

Critical values for two-tailed t-test: ±cdf t,d -1 (1-α/2)

(-∞, -cdf t,d -1 (1-α/2)] ∪ [cdf t,d -1 (1-α/2), ∞)

To decide the fate of the null hypothesis, just check if your T-score lies within the critical region:

If your T-score belongs to the critical region , reject the null hypothesis and accept the alternative hypothesis.

If your T-score is outside the critical region , then you don't have enough evidence to reject the null hypothesis.

How to use our t-test calculator

Choose the type of t-test you wish to perform:

A one-sample t-test (to test the mean of a single group against a hypothesized mean);

A two-sample t-test (to compare the means for two groups); or

A paired t-test (to check how the mean from the same group changes after some intervention).

Two-tailed;

Left-tailed; or

Right-tailed.

This t-test calculator allows you to use either the p-value approach or the critical regions approach to hypothesis testing!

Enter your T-score and the number of degrees of freedom . If you don't know them, provide some data about your sample(s): sample size, mean, and standard deviation, and our t-test calculator will compute the T-score and degrees of freedom for you .

Once all the parameters are present, the p-value, or critical region, will immediately appear underneath the t-test calculator, along with an interpretation!

One-sample t-test

The null hypothesis is that the population mean is equal to some value μ 0 \mu_0 μ 0 ​ .

The alternative hypothesis is that the population mean is:

• different from μ 0 \mu_0 μ 0 ​ ;
• smaller than μ 0 \mu_0 μ 0 ​ ; or
• greater than μ 0 \mu_0 μ 0 ​ .

One-sample t-test formula :

• μ 0 \mu_0 μ 0 ​ — Mean postulated in the null hypothesis;
• n n n — Sample size;
• x ˉ \bar{x} x ˉ — Sample mean; and
• s s s — Sample standard deviation.

Number of degrees of freedom in t-test (one-sample) = n − 1 n-1 n − 1 .

The null hypothesis is that the actual difference between these groups' means, μ 1 \mu_1 μ 1 ​ , and μ 2 \mu_2 μ 2 ​ , is equal to some pre-set value, Δ \Delta Δ .

The alternative hypothesis is that the difference μ 1 − μ 2 \mu_1 - \mu_2 μ 1 ​ − μ 2 ​ is:

• Different from Δ \Delta Δ ;
• Smaller than Δ \Delta Δ ; or
• Greater than Δ \Delta Δ .

In particular, if this pre-determined difference is zero ( Δ = 0 \Delta = 0 Δ = 0 ):

The null hypothesis is that the population means are equal.

The alternate hypothesis is that the population means are:

• μ 1 \mu_1 μ 1 ​ and μ 2 \mu_2 μ 2 ​ are different from one another;
• μ 1 \mu_1 μ 1 ​ is smaller than μ 2 \mu_2 μ 2 ​ ; and
• μ 1 \mu_1 μ 1 ​ is greater than μ 2 \mu_2 μ 2 ​ .

Formally, to perform a t-test, we should additionally assume that the variances of the two populations are equal (this assumption is called the homogeneity of variance ).

There is a version of a t-test that can be applied without the assumption of homogeneity of variance: it is called a Welch's t-test . For your convenience, we describe both versions.

Two-sample t-test if variances are equal

Use this test if you know that the two populations' variances are the same (or very similar).

Two-sample t-test formula (with equal variances) :

where s p s_p s p ​ is the so-called pooled standard deviation , which we compute as:

• Δ \Delta Δ — Mean difference postulated in the null hypothesis;
• n 1 n_1 n 1 ​ — First sample size;
• x ˉ 1 \bar{x}_1 x ˉ 1 ​ — Mean for the first sample;
• s 1 s_1 s 1 ​ — Standard deviation in the first sample;
• n 2 n_2 n 2 ​ — Second sample size;
• x ˉ 2 \bar{x}_2 x ˉ 2 ​ — Mean for the second sample; and
• s 2 s_2 s 2 ​ — Standard deviation in the second sample.

Number of degrees of freedom in t-test (two samples, equal variances) = n 1 + n 2 − 2 n_1 + n_2 - 2 n 1 ​ + n 2 ​ − 2 .

Two-sample t-test if variances are unequal (Welch's t-test)

Use this test if the variances of your populations are different.

Two-sample Welch's t-test formula if variances are unequal:

• s 1 s_1 s 1 ​ — Standard deviation in the first sample;
• s 2 s_2 s 2 ​ — Standard deviation in the second sample.

The number of degrees of freedom in a Welch's t-test (two-sample t-test with unequal variances) is very difficult to count. We can approximate it with the help of the following Satterthwaite formula :

Alternatively, you can take the smaller of n 1 − 1 n_1 - 1 n 1 ​ − 1 and n 2 − 1 n_2 - 1 n 2 ​ − 1 as a conservative estimate for the number of degrees of freedom.

🔎 The Satterthwaite formula for the degrees of freedom can be rewritten as a scaled weighted harmonic mean of the degrees of freedom of the respective samples: n 1 − 1 n_1 - 1 n 1 ​ − 1 and n 2 − 1 n_2 - 1 n 2 ​ − 1 , and the weights are proportional to the standard deviations of the corresponding samples.

As we commonly perform a paired t-test when we have data about the same subjects measured twice (before and after some treatment), let us adopt the convention of referring to the samples as the pre-group and post-group.

The null hypothesis is that the true difference between the means of pre- and post-populations is equal to some pre-set value, Δ \Delta Δ .

The alternative hypothesis is that the actual difference between these means is:

Typically, this pre-determined difference is zero. We can then reformulate the hypotheses as follows:

The null hypothesis is that the pre- and post-means are the same, i.e., the treatment has no impact on the population .

The alternative hypothesis:

• The pre- and post-means are different from one another (treatment has some effect);
• The pre-mean is smaller than the post-mean (treatment increases the result); or
• The pre-mean is greater than the post-mean (treatment decreases the result).

Paired t-test formula

In fact, a paired t-test is technically the same as a one-sample t-test! Let us see why it is so. Let x 1 , . . . , x n x_1, ... , x_n x 1 ​ , ... , x n ​ be the pre observations and y 1 , . . . , y n y_1, ... , y_n y 1 ​ , ... , y n ​ the respective post observations. That is, x i , y i x_i, y_i x i ​ , y i ​ are the before and after measurements of the i -th subject.

For each subject, compute the difference, d i : = x i − y i d_i := x_i - y_i d i ​ := x i ​ − y i ​ . All that happens next is just a one-sample t-test performed on the sample of differences d 1 , . . . , d n d_1, ... , d_n d 1 ​ , ... , d n ​ . Take a look at the formula for the T-score :

Δ \Delta Δ — Mean difference postulated in the null hypothesis;

n n n — Size of the sample of differences, i.e., the number of pairs;

x ˉ \bar{x} x ˉ — Mean of the sample of differences; and

s s s  — Standard deviation of the sample of differences.

Number of degrees of freedom in t-test (paired): n − 1 n - 1 n − 1

t-test vs Z-test

We use a Z-test when we want to test the population mean of a normally distributed dataset, which has a known population variance . If the number of degrees of freedom is large, then the t-Student distribution is very close to N(0,1).

Hence, if there are many data points (at least 30), you may swap a t-test for a Z-test, and the results will be almost identical. However, for small samples with unknown variance, remember to use the t-test because, in such cases, the t-Student distribution differs significantly from the N(0,1)!

🙋 Have you concluded you need to perform the z-test? Head straight to our z-test calculator !

What is a t-test?

A t-test is a widely used statistical test that analyzes the means of one or two groups of data. For instance, a t-test is performed on medical data to determine whether a new drug really helps.

What are different types of t-tests?

Different types of t-tests are:

• One-sample t-test;
• Two-sample t-test; and
• Paired t-test.

How to find the t value in a one sample t-test?

To find the t-value:

• Subtract the null hypothesis mean from the sample mean value.
• Divide the difference by the standard deviation of the sample.
• Multiply the resultant with the square root of the sample size.

.css-m482sy.css-m482sy{color:#2B3148;background-color:transparent;font-family:var(--calculator-ui-font-family),Verdana,sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-m482sy.css-m482sy:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-m482sy .js-external-link-button.link-like,.css-m482sy .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-m482sy .js-external-link-button.link-like:hover,.css-m482sy .js-external-link-anchor:hover,.css-m482sy .js-external-link-button.link-like:active,.css-m482sy .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-m482sy .js-external-link-button.link-like:focus-visible,.css-m482sy .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-m482sy p,.css-m482sy div{margin:0;display:block;}.css-m482sy pre{margin:0;display:block;}.css-m482sy pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-m482sy pre:not(:first-child){padding-top:8px;}.css-m482sy ul,.css-m482sy ol{display:block margin:0;padding-left:20px;}.css-m482sy ul li,.css-m482sy ol li{padding-top:8px;}.css-m482sy ul ul,.css-m482sy ol ul,.css-m482sy ul ol,.css-m482sy ol ol{padding-top:0;}.css-m482sy ul:not(:first-child),.css-m482sy ol:not(:first-child){padding-top:4px;} .css-1h42f0z{margin:auto;overflow:auto;overflow-wrap:break-word;word-break:break-word;}@font-face{font-family:'KaTeX_AMS';src:url(/katex-fonts/KaTeX_AMS-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_AMS-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_AMS-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Script';src:url(/katex-fonts/KaTeX_Script-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Script-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Script-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size1';src:url(/katex-fonts/KaTeX_Size1-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size1-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size1-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size2';src:url(/katex-fonts/KaTeX_Size2-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size2-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size2-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size3';src:url(/katex-fonts/KaTeX_Size3-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size3-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size3-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size4';src:url(/katex-fonts/KaTeX_Size4-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size4-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size4-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Typewriter';src:url(/katex-fonts/KaTeX_Typewriter-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Typewriter-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Typewriter-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}.css-1h42f0z .katex{font:normal 1.21em KaTeX_Main,Times New Roman,serif;line-height:1.2;text-indent:0;text-rendering:auto;}.css-1h42f0z .katex *{-ms-high-contrast-adjust:none!important;border-color:currentColor;}.css-1h42f0z .katex .katex-version::after{content:'0.13.13';}.css-1h42f0z .katex .katex-mathml{position:absolute;clip:rect(1px,1px,1px,1px);padding:0;border:0;height:1px;width:1px;overflow:hidden;}.css-1h42f0z .katex .katex-html>.newline{display:block;}.css-1h42f0z .katex .base{position:relative;display:inline-block;white-space:nowrap;width:-webkit-min-content;width:-moz-min-content;width:-webkit-min-content;width:-moz-min-content;width:min-content;}.css-1h42f0z .katex .strut{display:inline-block;}.css-1h42f0z .katex .textbf{font-weight:bold;}.css-1h42f0z .katex .textit{font-style:italic;}.css-1h42f0z .katex .textrm{font-family:KaTeX_Main;}.css-1h42f0z .katex .textsf{font-family:KaTeX_SansSerif;}.css-1h42f0z .katex .texttt{font-family:KaTeX_Typewriter;}.css-1h42f0z .katex .mathnormal{font-family:KaTeX_Math;font-style:italic;}.css-1h42f0z .katex .mathit{font-family:KaTeX_Main;font-style:italic;}.css-1h42f0z .katex .mathrm{font-style:normal;}.css-1h42f0z .katex .mathbf{font-family:KaTeX_Main;font-weight:bold;}.css-1h42f0z .katex .boldsymbol{font-family:KaTeX_Math;font-weight:bold;font-style:italic;}.css-1h42f0z .katex .amsrm{font-family:KaTeX_AMS;}.css-1h42f0z .katex .mathbb,.css-1h42f0z .katex .textbb{font-family:KaTeX_AMS;}.css-1h42f0z .katex .mathcal{font-family:KaTeX_Caligraphic;}.css-1h42f0z .katex .mathfrak,.css-1h42f0z .katex .textfrak{font-family:KaTeX_Fraktur;}.css-1h42f0z .katex .mathtt{font-family:KaTeX_Typewriter;}.css-1h42f0z .katex .mathscr,.css-1h42f0z .katex .textscr{font-family:KaTeX_Script;}.css-1h42f0z .katex .mathsf,.css-1h42f0z .katex .textsf{font-family:KaTeX_SansSerif;}.css-1h42f0z .katex .mathboldsf,.css-1h42f0z .katex .textboldsf{font-family:KaTeX_SansSerif;font-weight:bold;}.css-1h42f0z .katex .mathitsf,.css-1h42f0z .katex .textitsf{font-family:KaTeX_SansSerif;font-style:italic;}.css-1h42f0z .katex .mainrm{font-family:KaTeX_Main;font-style:normal;}.css-1h42f0z .katex .vlist-t{display:inline-table;table-layout:fixed;border-collapse:collapse;}.css-1h42f0z .katex .vlist-r{display:table-row;}.css-1h42f0z .katex .vlist{display:table-cell;vertical-align:bottom;position:relative;}.css-1h42f0z .katex .vlist>span{display:block;height:0;position:relative;}.css-1h42f0z .katex .vlist>span>span{display:inline-block;}.css-1h42f0z .katex .vlist>span>.pstrut{overflow:hidden;width:0;}.css-1h42f0z .katex .vlist-t2{margin-right:-2px;}.css-1h42f0z .katex .vlist-s{display:table-cell;vertical-align:bottom;font-size:1px;width:2px;min-width:2px;}.css-1h42f0z .katex .vbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:column;-ms-flex-direction:column;flex-direction:column;-webkit-align-items:baseline;-webkit-box-align:baseline;-ms-flex-align:baseline;align-items:baseline;}.css-1h42f0z .katex .hbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:100%;}.css-1h42f0z .katex .thinbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:0;max-width:0;}.css-1h42f0z .katex .msupsub{text-align:left;}.css-1h42f0z .katex .mfrac>span>span{text-align:center;}.css-1h42f0z .katex .mfrac .frac-line{display:inline-block;width:100%;border-bottom-style:solid;}.css-1h42f0z .katex .mfrac .frac-line,.css-1h42f0z .katex .overline .overline-line,.css-1h42f0z .katex .underline .underline-line,.css-1h42f0z .katex .hline,.css-1h42f0z .katex .hdashline,.css-1h42f0z .katex .rule{min-height:1px;}.css-1h42f0z .katex .mspace{display:inline-block;}.css-1h42f0z .katex .llap,.css-1h42f0z .katex .rlap,.css-1h42f0z .katex .clap{width:0;position:relative;}.css-1h42f0z .katex .llap>.inner,.css-1h42f0z .katex .rlap>.inner,.css-1h42f0z .katex .clap>.inner{position:absolute;}.css-1h42f0z .katex .llap>.fix,.css-1h42f0z .katex .rlap>.fix,.css-1h42f0z .katex .clap>.fix{display:inline-block;}.css-1h42f0z .katex .llap>.inner{right:0;}.css-1h42f0z .katex .rlap>.inner,.css-1h42f0z .katex .clap>.inner{left:0;}.css-1h42f0z .katex .clap>.inner>span{margin-left:-50%;margin-right:50%;}.css-1h42f0z .katex .rule{display:inline-block;border:solid 0;position:relative;}.css-1h42f0z .katex .overline .overline-line,.css-1h42f0z .katex .underline .underline-line,.css-1h42f0z .katex .hline{display:inline-block;width:100%;border-bottom-style:solid;}.css-1h42f0z .katex .hdashline{display:inline-block;width:100%;border-bottom-style:dashed;}.css-1h42f0z .katex .sqrt>.root{margin-left:0.27777778em;margin-right:-0.55555556em;}.css-1h42f0z .katex .sizing.reset-size1.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size1{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size1.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size2{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size1.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size3{font-size:1.4em;}.css-1h42f0z .katex .sizing.reset-size1.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size4{font-size:1.6em;}.css-1h42f0z .katex .sizing.reset-size1.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size5{font-size:1.8em;}.css-1h42f0z .katex .sizing.reset-size1.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size6{font-size:2em;}.css-1h42f0z .katex .sizing.reset-size1.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size7{font-size:2.4em;}.css-1h42f0z .katex .sizing.reset-size1.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size8{font-size:2.88em;}.css-1h42f0z .katex .sizing.reset-size1.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size9{font-size:3.456em;}.css-1h42f0z .katex .sizing.reset-size1.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size10{font-size:4.148em;}.css-1h42f0z .katex .sizing.reset-size1.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size11{font-size:4.976em;}.css-1h42f0z .katex .sizing.reset-size2.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size1{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size2.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size2{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size2.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size3{font-size:1.16666667em;}.css-1h42f0z .katex .sizing.reset-size2.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size4{font-size:1.33333333em;}.css-1h42f0z .katex .sizing.reset-size2.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size5{font-size:1.5em;}.css-1h42f0z .katex .sizing.reset-size2.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size6{font-size:1.66666667em;}.css-1h42f0z .katex .sizing.reset-size2.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size7{font-size:2em;}.css-1h42f0z .katex .sizing.reset-size2.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size8{font-size:2.4em;}.css-1h42f0z .katex .sizing.reset-size2.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size9{font-size:2.88em;}.css-1h42f0z .katex .sizing.reset-size2.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size10{font-size:3.45666667em;}.css-1h42f0z .katex .sizing.reset-size2.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size11{font-size:4.14666667em;}.css-1h42f0z .katex .sizing.reset-size3.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size1{font-size:0.71428571em;}.css-1h42f0z .katex .sizing.reset-size3.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size2{font-size:0.85714286em;}.css-1h42f0z .katex .sizing.reset-size3.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size3{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size3.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size4{font-size:1.14285714em;}.css-1h42f0z .katex .sizing.reset-size3.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size5{font-size:1.28571429em;}.css-1h42f0z .katex .sizing.reset-size3.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size6{font-size:1.42857143em;}.css-1h42f0z .katex .sizing.reset-size3.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size7{font-size:1.71428571em;}.css-1h42f0z .katex .sizing.reset-size3.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size8{font-size:2.05714286em;}.css-1h42f0z .katex .sizing.reset-size3.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size9{font-size:2.46857143em;}.css-1h42f0z .katex .sizing.reset-size3.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size10{font-size:2.96285714em;}.css-1h42f0z .katex .sizing.reset-size3.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size11{font-size:3.55428571em;}.css-1h42f0z .katex .sizing.reset-size4.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size1{font-size:0.625em;}.css-1h42f0z .katex .sizing.reset-size4.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size2{font-size:0.75em;}.css-1h42f0z .katex .sizing.reset-size4.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size3{font-size:0.875em;}.css-1h42f0z .katex .sizing.reset-size4.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size4{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size4.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size5{font-size:1.125em;}.css-1h42f0z .katex .sizing.reset-size4.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size6{font-size:1.25em;}.css-1h42f0z .katex .sizing.reset-size4.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size7{font-size:1.5em;}.css-1h42f0z .katex .sizing.reset-size4.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size8{font-size:1.8em;}.css-1h42f0z .katex .sizing.reset-size4.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size9{font-size:2.16em;}.css-1h42f0z .katex .sizing.reset-size4.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size10{font-size:2.5925em;}.css-1h42f0z .katex .sizing.reset-size4.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size11{font-size:3.11em;}.css-1h42f0z .katex .sizing.reset-size5.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size1{font-size:0.55555556em;}.css-1h42f0z .katex .sizing.reset-size5.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size2{font-size:0.66666667em;}.css-1h42f0z .katex .sizing.reset-size5.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size3{font-size:0.77777778em;}.css-1h42f0z .katex .sizing.reset-size5.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size4{font-size:0.88888889em;}.css-1h42f0z .katex .sizing.reset-size5.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size5{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size5.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size6{font-size:1.11111111em;}.css-1h42f0z .katex .sizing.reset-size5.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size7{font-size:1.33333333em;}.css-1h42f0z .katex .sizing.reset-size5.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size8{font-size:1.6em;}.css-1h42f0z .katex .sizing.reset-size5.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size9{font-size:1.92em;}.css-1h42f0z .katex .sizing.reset-size5.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size10{font-size:2.30444444em;}.css-1h42f0z .katex .sizing.reset-size5.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size11{font-size:2.76444444em;}.css-1h42f0z .katex .sizing.reset-size6.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size1{font-size:0.5em;}.css-1h42f0z .katex .sizing.reset-size6.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size2{font-size:0.6em;}.css-1h42f0z .katex .sizing.reset-size6.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size3{font-size:0.7em;}.css-1h42f0z .katex .sizing.reset-size6.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size4{font-size:0.8em;}.css-1h42f0z .katex .sizing.reset-size6.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size5{font-size:0.9em;}.css-1h42f0z .katex .sizing.reset-size6.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size6{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size6.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size7{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size6.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size8{font-size:1.44em;}.css-1h42f0z .katex .sizing.reset-size6.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size9{font-size:1.728em;}.css-1h42f0z .katex .sizing.reset-size6.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size10{font-size:2.074em;}.css-1h42f0z .katex .sizing.reset-size6.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size11{font-size:2.488em;}.css-1h42f0z .katex .sizing.reset-size7.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size1{font-size:0.41666667em;}.css-1h42f0z .katex .sizing.reset-size7.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size2{font-size:0.5em;}.css-1h42f0z .katex .sizing.reset-size7.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size3{font-size:0.58333333em;}.css-1h42f0z .katex .sizing.reset-size7.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size4{font-size:0.66666667em;}.css-1h42f0z .katex .sizing.reset-size7.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size5{font-size:0.75em;}.css-1h42f0z .katex .sizing.reset-size7.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size6{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size7.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size7{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size7.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size8{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size7.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size9{font-size:1.44em;}.css-1h42f0z .katex .sizing.reset-size7.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size10{font-size:1.72833333em;}.css-1h42f0z .katex .sizing.reset-size7.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size11{font-size:2.07333333em;}.css-1h42f0z .katex .sizing.reset-size8.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size1{font-size:0.34722222em;}.css-1h42f0z .katex .sizing.reset-size8.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size2{font-size:0.41666667em;}.css-1h42f0z .katex .sizing.reset-size8.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size3{font-size:0.48611111em;}.css-1h42f0z .katex .sizing.reset-size8.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size4{font-size:0.55555556em;}.css-1h42f0z .katex .sizing.reset-size8.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size5{font-size:0.625em;}.css-1h42f0z .katex .sizing.reset-size8.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size6{font-size:0.69444444em;}.css-1h42f0z .katex .sizing.reset-size8.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size7{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size8.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size8{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size8.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size9{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size8.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size10{font-size:1.44027778em;}.css-1h42f0z .katex .sizing.reset-size8.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size11{font-size:1.72777778em;}.css-1h42f0z .katex .sizing.reset-size9.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size1{font-size:0.28935185em;}.css-1h42f0z .katex .sizing.reset-size9.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size2{font-size:0.34722222em;}.css-1h42f0z .katex .sizing.reset-size9.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size3{font-size:0.40509259em;}.css-1h42f0z .katex .sizing.reset-size9.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size4{font-size:0.46296296em;}.css-1h42f0z .katex .sizing.reset-size9.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size5{font-size:0.52083333em;}.css-1h42f0z .katex .sizing.reset-size9.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size6{font-size:0.5787037em;}.css-1h42f0z .katex .sizing.reset-size9.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size7{font-size:0.69444444em;}.css-1h42f0z .katex .sizing.reset-size9.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size8{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size9.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size9{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size9.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size10{font-size:1.20023148em;}.css-1h42f0z .katex .sizing.reset-size9.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size11{font-size:1.43981481em;}.css-1h42f0z .katex .sizing.reset-size10.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size1{font-size:0.24108004em;}.css-1h42f0z .katex .sizing.reset-size10.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size2{font-size:0.28929605em;}.css-1h42f0z .katex .sizing.reset-size10.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size3{font-size:0.33751205em;}.css-1h42f0z .katex .sizing.reset-size10.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size4{font-size:0.38572806em;}.css-1h42f0z .katex .sizing.reset-size10.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size5{font-size:0.43394407em;}.css-1h42f0z .katex .sizing.reset-size10.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size6{font-size:0.48216008em;}.css-1h42f0z .katex .sizing.reset-size10.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size7{font-size:0.57859209em;}.css-1h42f0z .katex .sizing.reset-size10.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size8{font-size:0.69431051em;}.css-1h42f0z .katex .sizing.reset-size10.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size9{font-size:0.83317261em;}.css-1h42f0z .katex .sizing.reset-size10.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size10{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size10.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size11{font-size:1.19961427em;}.css-1h42f0z .katex .sizing.reset-size11.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size1{font-size:0.20096463em;}.css-1h42f0z .katex .sizing.reset-size11.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size2{font-size:0.24115756em;}.css-1h42f0z .katex .sizing.reset-size11.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size3{font-size:0.28135048em;}.css-1h42f0z .katex .sizing.reset-size11.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size4{font-size:0.32154341em;}.css-1h42f0z .katex .sizing.reset-size11.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size5{font-size:0.36173633em;}.css-1h42f0z .katex .sizing.reset-size11.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size6{font-size:0.40192926em;}.css-1h42f0z .katex .sizing.reset-size11.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size7{font-size:0.48231511em;}.css-1h42f0z .katex .sizing.reset-size11.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size8{font-size:0.57877814em;}.css-1h42f0z .katex .sizing.reset-size11.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size9{font-size:0.69453376em;}.css-1h42f0z .katex .sizing.reset-size11.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size10{font-size:0.83360129em;}.css-1h42f0z .katex .sizing.reset-size11.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size11{font-size:1em;}.css-1h42f0z .katex .delimsizing.size1{font-family:KaTeX_Size1;}.css-1h42f0z .katex .delimsizing.size2{font-family:KaTeX_Size2;}.css-1h42f0z .katex .delimsizing.size3{font-family:KaTeX_Size3;}.css-1h42f0z .katex .delimsizing.size4{font-family:KaTeX_Size4;}.css-1h42f0z .katex .delimsizing.mult .delim-size1>span{font-family:KaTeX_Size1;}.css-1h42f0z .katex .delimsizing.mult .delim-size4>span{font-family:KaTeX_Size4;}.css-1h42f0z .katex .nulldelimiter{display:inline-block;width:0.12em;}.css-1h42f0z .katex .delimcenter{position:relative;}.css-1h42f0z .katex .op-symbol{position:relative;}.css-1h42f0z .katex .op-symbol.small-op{font-family:KaTeX_Size1;}.css-1h42f0z .katex .op-symbol.large-op{font-family:KaTeX_Size2;}.css-1h42f0z .katex .op-limits>.vlist-t{text-align:center;}.css-1h42f0z .katex .accent>.vlist-t{text-align:center;}.css-1h42f0z .katex .accent .accent-body{position:relative;}.css-1h42f0z .katex .accent .accent-body:not(.accent-full){width:0;}.css-1h42f0z .katex .overlay{display:block;}.css-1h42f0z .katex .mtable .vertical-separator{display:inline-block;min-width:1px;}.css-1h42f0z .katex .mtable .arraycolsep{display:inline-block;}.css-1h42f0z .katex .mtable .col-align-c>.vlist-t{text-align:center;}.css-1h42f0z .katex .mtable .col-align-l>.vlist-t{text-align:left;}.css-1h42f0z .katex .mtable .col-align-r>.vlist-t{text-align:right;}.css-1h42f0z .katex .svg-align{text-align:left;}.css-1h42f0z .katex svg{display:block;position:absolute;width:100%;height:inherit;fill:currentColor;stroke:currentColor;fill-rule:nonzero;fill-opacity:1;stroke-width:1;stroke-linecap:butt;stroke-linejoin:miter;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1;}.css-1h42f0z .katex svg path{stroke:none;}.css-1h42f0z .katex img{border-style:none;min-width:0;min-height:0;max-width:none;max-height:none;}.css-1h42f0z .katex .stretchy{width:100%;display:block;position:relative;overflow:hidden;}.css-1h42f0z .katex .stretchy::before,.css-1h42f0z .katex .stretchy::after{content:'';}.css-1h42f0z .katex .hide-tail{width:100%;position:relative;overflow:hidden;}.css-1h42f0z .katex .halfarrow-left{position:absolute;left:0;width:50.2%;overflow:hidden;}.css-1h42f0z .katex .halfarrow-right{position:absolute;right:0;width:50.2%;overflow:hidden;}.css-1h42f0z .katex .brace-left{position:absolute;left:0;width:25.1%;overflow:hidden;}.css-1h42f0z .katex .brace-center{position:absolute;left:25%;width:50%;overflow:hidden;}.css-1h42f0z .katex .brace-right{position:absolute;right:0;width:25.1%;overflow:hidden;}.css-1h42f0z .katex .x-arrow-pad{padding:0 0.5em;}.css-1h42f0z .katex .cd-arrow-pad{padding:0 0.55556em 0 0.27778em;}.css-1h42f0z .katex .x-arrow,.css-1h42f0z .katex .mover,.css-1h42f0z .katex .munder{text-align:center;}.css-1h42f0z .katex .boxpad{padding:0 0.3em 0 0.3em;}.css-1h42f0z .katex .fbox,.css-1h42f0z .katex .fcolorbox{box-sizing:border-box;border:0.04em solid;}.css-1h42f0z .katex .cancel-pad{padding:0 0.2em 0 0.2em;}.css-1h42f0z .katex .cancel-lap{margin-left:-0.2em;margin-right:-0.2em;}.css-1h42f0z .katex .sout{border-bottom-style:solid;border-bottom-width:0.08em;}.css-1h42f0z .katex .angl{box-sizing:border-box;border-top:0.049em solid;border-right:0.049em solid;margin-right:0.03889em;}.css-1h42f0z .katex .anglpad{padding:0 0.03889em 0 0.03889em;}.css-1h42f0z .katex .eqn-num::before{counter-increment:katexEqnNo;content:'(' counter(katexEqnNo) ')';}.css-1h42f0z .katex .mml-eqn-num::before{counter-increment:mmlEqnNo;content:'(' counter(mmlEqnNo) ')';}.css-1h42f0z .katex .mtr-glue{width:50%;}.css-1h42f0z .katex .cd-vert-arrow{display:inline-block;position:relative;}.css-1h42f0z .katex .cd-label-left{display:inline-block;position:absolute;right:calc(50% + 0.3em);text-align:left;}.css-1h42f0z .katex .cd-label-right{display:inline-block;position:absolute;left:calc(50% + 0.3em);text-align:right;}.css-1h42f0z .katex-display{display:block;margin:1em 0;text-align:center;}.css-1h42f0z .katex-display>.katex{display:block;white-space:nowrap;}.css-1h42f0z .katex-display>.katex>.katex-html{display:block;position:relative;}.css-1h42f0z .katex-display>.katex>.katex-html>.tag{position:absolute;right:0;}.css-1h42f0z .katex-display.leqno>.katex>.katex-html>.tag{left:0;right:auto;}.css-1h42f0z .katex-display.fleqn>.katex{text-align:left;padding-left:2em;}.css-1h42f0z body{counter-reset:katexEqnNo mmlEqnNo;}.css-1h42f0z .link-like{color:#007bff;-webkit-text-decoration:underline;text-decoration:underline;}.css-1h42f0z .text-overline{-webkit-text-decoration:overline;text-decoration:overline;}.css-1h42f0z code,.css-1h42f0z kbd,.css-1h42f0z pre,.css-1h42f0z samp{font-family:monospace;}.css-1h42f0z code{padding:2px 4px;color:#444;background:#ddd;border-radius:4px;}.css-1h42f0z figcaption,.css-1h42f0z caption{text-align:center;}.css-1h42f0z figcaption{font-size:12px;font-style:italic;overflow:hidden;}.css-1h42f0z h3{font-size:1.75rem;}.css-1h42f0z h4{font-size:1.5rem;}.css-1h42f0z .mathBlock{font-size:24px;-webkit-padding-start:4px;padding-inline-start:4px;}.css-1h42f0z .mathBlock .katex{font-size:24px;text-align:left;}.css-1h42f0z .math-inline{background-color:#f0f0f0;display:inline-block;font-size:inherit;padding:0 3px;}.css-1h42f0z .videoBlock,.css-1h42f0z .imageBlock{margin-bottom:16px;}.css-1h42f0z .imageBlock__image-align--left,.css-1h42f0z .videoBlock__video-align--left{float:left;}.css-1h42f0z .imageBlock__image-align--right,.css-1h42f0z .videoBlock__video-align--right{float:right;}.css-1h42f0z .imageBlock__image-align--center,.css-1h42f0z .videoBlock__video-align--center{display:block;margin-left:auto;margin-right:auto;clear:both;}.css-1h42f0z .imageBlock__image-align--none,.css-1h42f0z .videoBlock__video-align--none{clear:both;margin-left:0;margin-right:0;}.css-1h42f0z .videoBlock__video--wrapper{position:relative;padding-bottom:56.25%;height:0;}.css-1h42f0z .videoBlock__video--wrapper iframe{position:absolute;top:0;left:0;width:100%;height:100%;}.css-1h42f0z .videoBlock__caption{text-align:left;}.css-1h42f0z table{width:-webkit-max-content;width:-moz-max-content;width:max-content;}.css-1h42f0z .tableBlock{max-width:100%;margin-bottom:1rem;overflow-y:scroll;}.css-1h42f0z .tableBlock thead,.css-1h42f0z .tableBlock thead th{border-bottom:1px solid #333!important;}.css-1h42f0z .tableBlock th,.css-1h42f0z .tableBlock td{padding:10px;text-align:left;}.css-1h42f0z .tableBlock th{font-weight:bold!important;}.css-1h42f0z .tableBlock caption{caption-side:bottom;color:#555;font-size:12px;font-style:italic;text-align:center;}.css-1h42f0z .tableBlock caption>p{margin:0;}.css-1h42f0z .tableBlock th>p,.css-1h42f0z .tableBlock td>p{margin:0;}.css-1h42f0z .tableBlock [data-background-color='aliceblue']{background-color:#f0f8ff;color:#000;}.css-1h42f0z .tableBlock [data-background-color='black']{background-color:#000;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='chocolate']{background-color:#d2691e;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='cornflowerblue']{background-color:#6495ed;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='crimson']{background-color:#dc143c;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='darkblue']{background-color:#00008b;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='darkseagreen']{background-color:#8fbc8f;color:#000;}.css-1h42f0z .tableBlock [data-background-color='deepskyblue']{background-color:#00bfff;color:#000;}.css-1h42f0z .tableBlock [data-background-color='gainsboro']{background-color:#dcdcdc;color:#000;}.css-1h42f0z .tableBlock [data-background-color='grey']{background-color:#808080;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='lemonchiffon']{background-color:#fffacd;color:#000;}.css-1h42f0z .tableBlock [data-background-color='lightpink']{background-color:#ffb6c1;color:#000;}.css-1h42f0z .tableBlock [data-background-color='lightsalmon']{background-color:#ffa07a;color:#000;}.css-1h42f0z .tableBlock [data-background-color='lightskyblue']{background-color:#87cefa;color:#000;}.css-1h42f0z .tableBlock [data-background-color='mediumblue']{background-color:#0000cd;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='omnigrey']{background-color:#f0f0f0;color:#000;}.css-1h42f0z .tableBlock [data-background-color='white']{background-color:#fff;color:#000;}.css-1h42f0z .tableBlock [data-text-align='center']{text-align:center;}.css-1h42f0z .tableBlock [data-text-align='left']{text-align:left;}.css-1h42f0z .tableBlock [data-text-align='right']{text-align:right;}.css-1h42f0z .tableBlock [data-vertical-align='bottom']{vertical-align:bottom;}.css-1h42f0z .tableBlock [data-vertical-align='middle']{vertical-align:middle;}.css-1h42f0z .tableBlock [data-vertical-align='top']{vertical-align:top;}.css-1h42f0z .tableBlock__font-size--xxsmall{font-size:10px;}.css-1h42f0z .tableBlock__font-size--xsmall{font-size:12px;}.css-1h42f0z .tableBlock__font-size--small{font-size:14px;}.css-1h42f0z .tableBlock__font-size--large{font-size:18px;}.css-1h42f0z .tableBlock__border--some tbody tr:not(:last-child){border-bottom:1px solid #e2e5e7;}.css-1h42f0z .tableBlock__border--bordered td,.css-1h42f0z .tableBlock__border--bordered th{border:1px solid #e2e5e7;}.css-1h42f0z .tableBlock__border--borderless tbody+tbody,.css-1h42f0z .tableBlock__border--borderless td,.css-1h42f0z .tableBlock__border--borderless th,.css-1h42f0z .tableBlock__border--borderless tr,.css-1h42f0z .tableBlock__border--borderless thead,.css-1h42f0z .tableBlock__border--borderless thead th{border:0!important;}.css-1h42f0z .tableBlock:not(.tableBlock__table-striped) tbody tr{background-color:unset!important;}.css-1h42f0z .tableBlock__table-striped tbody tr:nth-of-type(odd){background-color:#f9fafc!important;}.css-1h42f0z .tableBlock__table-compactl th,.css-1h42f0z .tableBlock__table-compact td{padding:3px!important;}.css-1h42f0z .tableBlock__full-size{width:100%;}.css-1h42f0z .textBlock{margin-bottom:16px;}.css-1h42f0z .textBlock__text-formatting--finePrint{font-size:12px;}.css-1h42f0z .textBlock__text-infoBox{padding:0.75rem 1.25rem;margin-bottom:1rem;border:1px solid transparent;border-radius:0.25rem;}.css-1h42f0z .textBlock__text-infoBox p{margin:0;}.css-1h42f0z .textBlock__text-infoBox--primary{background-color:#cce5ff;border-color:#b8daff;color:#004085;}.css-1h42f0z .textBlock__text-infoBox--secondary{background-color:#e2e3e5;border-color:#d6d8db;color:#383d41;}.css-1h42f0z .textBlock__text-infoBox--success{background-color:#d4edda;border-color:#c3e6cb;color:#155724;}.css-1h42f0z .textBlock__text-infoBox--danger{background-color:#f8d7da;border-color:#f5c6cb;color:#721c24;}.css-1h42f0z .textBlock__text-infoBox--warning{background-color:#fff3cd;border-color:#ffeeba;color:#856404;}.css-1h42f0z .textBlock__text-infoBox--info{background-color:#d1ecf1;border-color:#bee5eb;color:#0c5460;}.css-1h42f0z .textBlock__text-infoBox--dark{background-color:#d6d8d9;border-color:#c6c8ca;color:#1b1e21;}.css-1h42f0z.css-1h42f0z{color:#2B3148;background-color:transparent;font-family:var(--calculator-ui-font-family),Verdana,sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-1h42f0z.css-1h42f0z:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-1h42f0z .js-external-link-button.link-like,.css-1h42f0z .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-1h42f0z .js-external-link-button.link-like:hover,.css-1h42f0z .js-external-link-anchor:hover,.css-1h42f0z .js-external-link-button.link-like:active,.css-1h42f0z .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-1h42f0z .js-external-link-button.link-like:focus-visible,.css-1h42f0z .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-1h42f0z p,.css-1h42f0z div{margin:0;display:block;}.css-1h42f0z pre{margin:0;display:block;}.css-1h42f0z pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-1h42f0z pre:not(:first-child){padding-top:8px;}.css-1h42f0z ul,.css-1h42f0z ol{display:block margin:0;padding-left:20px;}.css-1h42f0z ul li,.css-1h42f0z ol li{padding-top:8px;}.css-1h42f0z ul ul,.css-1h42f0z ol ul,.css-1h42f0z ul ol,.css-1h42f0z ol ol{padding-top:0;}.css-1h42f0z ul:not(:first-child),.css-1h42f0z ol:not(:first-child){padding-top:4px;} Test setup

Choose test type

t-test for the population mean, μ, based on one independent sample . Null hypothesis H 0 : μ = μ 0  

Alternative hypothesis H 1

Test details

Significance level α

The probability that we reject a true H 0 (type I error).

Degrees of freedom

Calculated as sample size minus one.

Test results

Hypothesis Testing Calculator

Type ii error.

The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is known as a t test and we use the t distribution. Use of the t distribution relies on the degrees of freedom, which is equal to the sample size minus one. Furthermore, if the population standard deviation σ is unknown, the sample standard deviation s is used instead. To switch from σ known to σ unknown, click on $\boxed{\sigma}$ and select $\boxed{s}$ in the Hypothesis Testing Calculator.

Next, the test statistic is used to conduct the test using either the p-value approach or critical value approach. The particular steps taken in each approach largely depend on the form of the hypothesis test: lower tail, upper tail or two-tailed. The form can easily be identified by looking at the alternative hypothesis (H a ). If there is a less than sign in the alternative hypothesis then it is a lower tail test, greater than sign is an upper tail test and inequality is a two-tailed test. To switch from a lower tail test to an upper tail or two-tailed test, click on $\boxed{\geq}$ and select $\boxed{\leq}$ or $\boxed{=}$, respectively.

In the p-value approach, the test statistic is used to calculate a p-value. If the test is a lower tail test, the p-value is the probability of getting a value for the test statistic at least as small as the value from the sample. If the test is an upper tail test, the p-value is the probability of getting a value for the test statistic at least as large as the value from the sample. In a two-tailed test, the p-value is the probability of getting a value for the test statistic at least as unlikely as the value from the sample.

To test the hypothesis in the p-value approach, compare the p-value to the level of significance. If the p-value is less than or equal to the level of signifance, reject the null hypothesis. If the p-value is greater than the level of significance, do not reject the null hypothesis. This method remains unchanged regardless of whether it's a lower tail, upper tail or two-tailed test. To change the level of significance, click on $\boxed{.05}$. Note that if the test statistic is given, you can calculate the p-value from the test statistic by clicking on the switch symbol twice.

In the critical value approach, the level of significance ($\alpha$) is used to calculate the critical value. In a lower tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the lower tail of the sampling distribution of the test statistic. In an upper tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the upper tail of the sampling distribution of the test statistic. In a two-tailed test, the critical values are the values of the test statistic providing areas of $\alpha / 2$ in the lower and upper tail of the sampling distribution of the test statistic.

To test the hypothesis in the critical value approach, compare the critical value to the test statistic. Unlike the p-value approach, the method we use to decide whether to reject the null hypothesis depends on the form of the hypothesis test. In a lower tail test, if the test statistic is less than or equal to the critical value, reject the null hypothesis. In an upper tail test, if the test statistic is greater than or equal to the critical value, reject the null hypothesis. In a two-tailed test, if the test statistic is less than or equal the lower critical value or greater than or equal to the upper critical value, reject the null hypothesis.

When conducting a hypothesis test, there is always a chance that you come to the wrong conclusion. There are two types of errors you can make: Type I Error and Type II Error. A Type I Error is committed if you reject the null hypothesis when the null hypothesis is true. Ideally, we'd like to accept the null hypothesis when the null hypothesis is true. A Type II Error is committed if you accept the null hypothesis when the alternative hypothesis is true. Ideally, we'd like to reject the null hypothesis when the alternative hypothesis is true.

Hypothesis testing is closely related to the statistical area of confidence intervals. If the hypothesized value of the population mean is outside of the confidence interval, we can reject the null hypothesis. Confidence intervals can be found using the Confidence Interval Calculator . The calculator on this page does hypothesis tests for one population mean. Sometimes we're interest in hypothesis tests about two population means. These can be solved using the Two Population Calculator . The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page.

Two Sample T-Test Calculator (Pooled-Variance)

Enter sample data, information, assumptions, required sample data.

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)
• Statistics and probability
• T-test calculator

T-Test calculator

The Student's t-test is used to determine if means of two data sets differ significantly. This calculator will generate a step by step explanation on how to apply t – test.

Get Widget Code

• Long Division
• Evaluate Expressions
• Fraction Calculator
• Greatest Common Divisor GCD
• Least Common Multiple LCM
• Prime Factorization
• Scientific Notation
• Percentage Calculator
• Dec / Bin / Hex
• Factoring Polynomials
• Polynomial Roots
• Synthetic Division
• Polynomial Operations
• Graphing Polynomials
• Simplify Polynomials
• Generate From Roots
• Simplify Expression
• Multiplication / Division
• Addition / Subtraction
• Rationalize Denominator
• Simplifying
• Quadratic Equations Solver
• Polynomial Equations
• Solving Equations - With Steps
• Solving (with steps)
• Quadratic Plotter
• Factoring Trinomials
• Equilateral Triangle
• Right Triangle
• Oblique Triangle
• Square Calculator
• Rectangle Calculator
• Circle Calculator
• Hexagon Calculator
• Rhombus Calculator
• Trapezoid Calculator
• Triangular Prism
• Distance calculator
• Midpoint Calculator
• Triangle Calculator
• Graphing Lines
• Lines Intersection
• Two Point Form
• Line-Point Distance
• Parallel/Perpendicular
• Circle Equation
• Circle From 3 Points
• Circle-line Intersection
• Modulus, inverse, polar form
• Vectors (2D & 3D)
• Add, Subtract, Multiply
• Determinant Calculator
• Matrix Inverse
• Characteristic Polynomial
• Eigenvalues
• Eigenvectors
• Matrix Decomposition
• Limit Calculator
• Derivative Calculator
• Integral Calculator
• Arithmetic Sequences
• Geometric Sequences
• Find n th Term
• Degrees to Radians
• Trig. Equations
• Probability Calculator
• Probability Distributions
• Descriptive Statistics
• Standard Deviation
• Z - score Calculator
• Normal Distribution
• T-Test Calculator
• Correlation & Regression
• Simple Interest
• Compound Interest
• Amortization Calculator
• Annuity Calculator
• Work Problems

Hire MATHPORTAL experts to do math homework for you.

Prices start at $3 per problem.

Twelve younger adults and twelve older adults conducted a life satisfaction test. The data are presented in the table below. Compute the appropriate t-test.

Are the means between two data sets are significantly different at level $\alpha < 0.05$.

Standard deviation calculator – Widget Code

Feel free to copy the widget code below and paste it into your website or blog. The widget will look like the example below.

Widget preview: Standard deviation calculator

Copy code to clipboard

Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .

If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]

Email (optional)

Two sample t test calculator

Welcome to our Two Sample T Test Calculator, the ideal tool for comparing mean values from two independent samples. This calculator calculates test statistics, p-values, critical values, judgments, and conclusions using both equal and unequal variance approaches. This tool is intended to help students, researchers, and data analysts simplify their statistical analyses.

Enter below values for sample 1 :

Enter below values for sample 2:

Related Calculators :

• List of all calculator
• P-value calculator
• Critical value Calculator

What is a Two Sample T Test?

A Two Sample T Test is used to see if there is a significant difference in the means of two independent groups. This test is frequently used in experiments and research to compare two groups and draw conclusions about the population mean.

Features of Our Two Sample T-Test Calculator

• Direct Data Entry: Enter each sample's raw data values directly into the calculator.
• Summary Statistics: If you have summary statistics rather than raw data, please provide the sample size, mean, and standard deviation.
• Hypothesis Testing: Determine whether your null and alternative hypotheses are two-tailed, right-tailed, or left-tailed.
• Significance Level: Enter the significance level (alpha) for the test.
• Variance Type: For more accurate results, select either equal or unequal variance.
• Detailed Results: Receive complete results, including test statistics, p-values, critical values, and decision-making conclusions.

How To Use The Calculator

Select Data Type: Determine whether you have raw data values or summary statistics.

Enter Data: Fill in the data values or summary statistics for both samples.

Hypothesis Selection: Determine the relevant null and alternative hypotheses for your test.

Set the Significance Level: The alpha level is used to set the threshold for statistical significance.

Variance Type: Determine whether the variances of the two samples are equal or unequal.

Calculate: To view the results, simply click the "Calculate" button.

Example Use Cases

Our Two Sample T-Test Calculator can be applied in various fields, including:

• Medical Research: Determine the efficacy of two different drugs.
• Education: Compare test scores from two distinct teaching approaches.
• Marketing: Evaluate the effectiveness of two marketing efforts.

Why Use Our Calculator?

• Accuracy: Our calculator can perform precise estimates for both equal and unequal variance cases.
• Ease of Use: A user-friendly interface with clear directions and inputs.
• Comprehensive Results: Detailed output, including statistical computations and decision-making advice.

Frequently Asked Questions

Q: What is the difference between equal and unequal variances? A: Equal variance assumes that the two populations have equal variance, whereas unequal variance does not make this assumption. Selecting the proper option guarantees accurate results.

Q: How do I determine whether to conduct a two-tailed, right-tailed, or left-tailed test? A: It depends on your research hypothesis. If you want to find a significant difference, conduct a two-tailed test. If you predict the first sample's mean to be greater than the second, perform a right-tailed test. If you predict the first sample's mean to be less than the second, perform a left-tailed test.

Easy Hypothesis Test Calculator for Z and T Tests

Hypothesis testing calculator, what is hypothesis testing.

Hypothesis testing is a statistical method used to make inferences about population parameters based on sample data. It involves formulating two competing hypotheses about a population parameter: the null hypothesis (H₀) and the alternative hypothesis (H₁ or Hₐ). The null hypothesis typically represents no effect or no difference, while the alternative hypothesis represents the presence of an effect or a difference.

The process of hypothesis testing involves collecting sample data, calculating test statistics, and determining the probability (p-value) of obtaining such results if the null hypothesis were true. Based on this probability and a predetermined significance level (α), researchers can decide whether to reject the null hypothesis in favor of the alternative hypothesis or fail to reject the null hypothesis.

How to Use the Hypothesis Testing Calculator?

1. Select the Test Type Choose between a Z-test (for known population standard deviation) or a T-test (for unknown population standard deviation).

2. Choose the Hypothesis Type Select from two-tailed (≠), left-tailed (<), or right-tailed (>) tests, depending on your research question.

3. Enter Sample Mean (x ̄) Input the mean of your sample data.

4. Enter Population Mean (μ ₀) Input the hypothesized population mean (null hypothesis value).

5. Enter Sample Size (n) Input the number of observations in your sample.

6. Enter Standard Deviation For Z-tests, enter the known population standard deviation. For T-tests, enter the sample standard deviation.

7. Set Significance Level (α) Enter your desired significance level (default is 0.05).

8. Click "Calculate" The tool will compute and display the results.

9. Interpret the Results

• Test Statistic: The calculated Z or T value.
• P-Value: The probability of obtaining test results at least as extreme as the observed results, assuming the null hypothesis is true.
• Critical Value: The threshold value for rejecting the null hypothesis.
• Decision: Whether to reject or fail to reject the null hypothesis.
• Interpretation: A brief explanation of the statistical findings.

This calculator simplifies the process of hypothesis testing by automating complex calculations. It's particularly useful for students, researchers, and professionals who need to perform quick statistical analyses. The tool supports both one-sample Z-tests and T-tests, accommodating scenarios where the population standard deviation is known or unknown.

By providing a user-friendly interface and clear results, this calculator helps users make informed decisions based on their data. It's important to note that while this tool provides valuable statistical information, the interpretation and application of results should always consider the broader context of the research question and the limitations of the data.

Remember that hypothesis testing is just one part of the scientific process. It should be used in conjunction with other statistical methods, careful experimental design, and thoughtful interpretation of results to draw meaningful conclusions from data.

Related Tools

One rep max calculator: estimate your 1rm easily, hcf calculator: find greatest common factor instantly, bike saddle height calculator: find your perfect fit, easy differential equation calculator | quick results, slugging percentage calculator | baseball stats tool, uk tree removal cost calculator | instant estimate.

Two Sample t test calculator

Instructions: Use this calculator to work on a two-samples t-test, showing all the steps. In order to run the test, you need two provide two independent samples in the spreadsheet below. You can either type the data or simply paste them from Excel.

Two-sample t-test calculator

This calculator will allow you to get all the details and steps related to the calculation of a two-sample t-test. The process for conducting a t-test is relatively simple, but it requires lots of calculations often times, which will be shown to you in detail by this calculator.

The first step in using this calculator is to use the spreadsheet in which you need to either type or paste the data. You can have your data originally in Excel and then paste it in, no problem. After you type or paste the data, all you need to do is to click on "Calculate" to get all the steps shown.

There are lots of subtleties involved in the process of conducting a t-test. There are certain distribution assumptions that need to be met, it needs to be assessed whether or not the population standard deviation can be assumed to be equal . Once the assumption requirements are cleared, we can proceed with the test statistic calculation.

Independent t-test Calculator with Samples

Usually there are two different forms that can lead to calculating an independent t-test. You can either have two samples, or you can have the data already summarized. For the latter, use this independent t-test calculator with summarized data .

For the case of two samples, you will first need to conduct descriptive statistics calculations in order to get a summary of the provided independent samples.

Steps for running a independent t-test

• Step 1: Identify the samples provided. Those samples need to be at least approximately normal
• Step 2: Usually it is out of the scope of what is required to conduct formal statistical tests, in which case you would like to create a histogram of the samples, to see if they look at least approximately bell-shaped
• Step 3: If you do need to formally test for the normality of the samples, you can use this normality test calculator
• Step 4: Once you have cleared the assumptions (if needed), you can proceed with running the actual t-test
• Step 5: One previous step that is needed too is that about assessing whether the population standard deviations can be assumed to be equal or not

Why do we need to test for the equality of population variances? This is because there is the need to find the standard error for the test, and it turns out that the optimal choice for the standard error depends on whether the population standard deviations are equal or not.

That is a rather technical topic, but in layman terms, if the population variances are equal, then the best choice is to basically pool the available sample variances to get a good standard error estimate.

But if they are not equal, things get a bit more complicated, and some technical corrections are needed, which is what you see reflected in the fact that the formula used is different, and the degrees of freedom are different too.

What is the t-value in a 2 sample test?

The formula used for the independent samples t-test will depend upon whether or not the population variances are assumed to be equal. If they are assumed to be unequal, the formula used is

But, if the population variances are assumed to be equal, you then need to use the following formula:

Equality of Population Variances

When to assume equality of population variances? There is a formal test, which is the F-test for equality of variances, which is conducted by this calculator if you select the option.

Sometimes, different rules of thumb are used, like taking the highest of sample variance, divide by the lowest sample variance and assume that the population variances are equal if this ratio is less than 3, or another rule like that. That is not a completely bad idea, but if you really need to know, it is best to run a formal test.

What are the steps for computing the t-test formula

• Step 1: Assess whether or not the population variances are equal. Run a F-test for equality of variances if needed
• Step 2: Depending on whether equality of population variances is assumed or not, you will choose the right formula for the t-test
• Step 3: For unequal population variances, you use \(t = \frac{\bar X_1 - \bar X_2}{\sqrt{ \frac{s_1^2}{n_1} + \frac{s_2^2}{n_2} }}\)
• Step 4: For equal population variances, you use \(t = \frac{\bar X_1 - \bar X_2}{\sqrt{ \frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2-2}(\frac{1}{n_1}+\frac{1}{n_2}) } }\)
• Step 5: Based on the number of degrees of freedom and type of tail, you compute the corresponding p-value, and if the p-value is less than the significance level, the null hypothesis is rejected

The number of degrees of freedom when equal population variances are assumed is \(df = n_1 + n_2\), where \(n_1\) and \(n_2\) are the corresponding sample sizes . Now for unequal variances, the calculation of degrees of freedoms is a lot more complicated.

Is this a t-test calculator with steps?

Yes! This calculator will show you all the steps of the way, from the calculation of descriptive statistics, to the testing for equality of variances (if required) to the use of the proper t-test formula to the discussion and conclusions.

Why is this test statistic calculator useful? Time! You will save lots of time because an independent samples t-test requires a whole lot of calculations.

What is an example of a 2 sample t-test?

Suppose that a teacher believes that the average height of eighth graders for two different schools. There is a sample of n = 10 kids for each school, for which their sample heights (in inches) are available:

School 1: 60, 62, 59, 63, 65, 64, 68, 67, 61, 60

School 1: 60, 61, 61, 61, 60, 59, 59, 60, 60, 59

Is there enough evidence to claim that the population mean heights for two schools are different, at the 0.05 significance level?

Solution: The following information sample information has been provided:

In order to conduct a two-independent samples t-test, we need to compute descriptive statistics of the samples:

Summarizing, the following descriptive statistics will be used in the calculation of the t-statistic:

The following information has been provided:

(1) Null and Alternative Hypotheses

The following null and alternative hypotheses need to be tested:

This corresponds to a two-tailed test, for which a t-test for two population means, with two independent samples, with unknown population standard deviations will be used.

Testing for Equality of Variances

A F-test is used to test for the equality of variances. The following F-ratio is obtained:

The critical values are \(F_L = 0.248\) and \(F_U = 4.026\), and since \(F = 14.15\), then the null hypothesis of equal variances is rejected.

(2) Rejection Region

Based on the information provided, the significance level is \(\alpha = 0.05\), and the degrees of freedom are \(df = 10.266\). In fact, the degrees of freedom are computed as follows, assuming that the population variances are unequal:

Hence, it is found that the critical value for this two-tailed test is \(t_c = 2.22\), for \(\alpha = 0.05\) and \(df = 10.266\).

The rejection region for this two-tailed test is \(R = \{t: |t| > 2.22\}\).

(3) Test Statistics

Since it is assumed that the population variances are unequal, the t-statistic is computed as follows:

(4) Decision about the null hypothesis

Since it is observed that \(|t| = 2.886 > t_c = 2.22\), it is then concluded that the null hypothesis is rejected.

Using the P-value approach: The p-value is \(p = 0.0158\), and since \(p = 0.0158 < 0.05\), it is concluded that the null hypothesis is rejected.

(5) Conclusion

It is concluded that the null hypothesis Ho is rejected. Therefore, there is enough evidence to claim that the population mean \(\mu_1\) is different than \(\mu_2\), at the \(\alpha = 0.05\) significance level.

Confidence Interval

The 95% confidence interval is \(0.669 < \mu < 5.131\).

Graphically

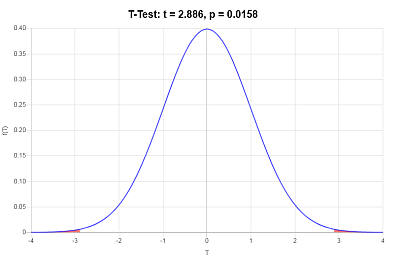
Other statistical tests of interest

There is an abundance of related statistical tests that you can use. You can try for example this paired t-test calculator . Also you can you this t-test for two samples when you have summarized sample data instead. In that case, the sample data provided is usually the sample means , sample standard deviations and sample sizes.

Other type of t-test calculators include the t-test for one sample . For different types of statistics, you can try this ANOVA calculator , which is similar to the t-test only that with ANOVA you can compare more than 2 groups.

Related Calculators

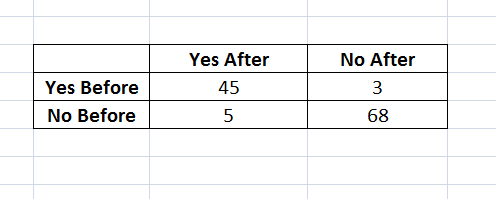
log in to your account

Reset password.

• Calculators
• Descriptive Statistics
• Merchandise
• Which Statistics Test?

P Value from Z Score Calculator

This is very easy: just stick your Z score in the box marked Z score, select your significance level and whether you're testing a one or two-tailed hypothesis (if you're not sure, go with the defaults), then press the button!

If you need to derive a Z score from raw data, you can find a Z test calculator here .

Enter your z score value, and then press the button.

Additional Z Statistic Calculators

If you're interested in using the z statistic for hypothesis testing and the like, then we have a number of other calculators that might help you.

Z-Test Calculator for a Single Sample Z-Test Calculator for 2 Population Proportions Z Score Calculator for a Single Raw Value (Includes z from p )