ratio problem solving activity

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Ratio problem solving

Here you will learn about ratio problem solving, including how to set up and solve problems. You will also look at real life ratio word problems.

Students will first learn about ratio problem solving as part of ratio and proportion in 6 th grade and 7 th grade.

What is ratio problem solving?

Ratio problem solving is a collection of ratio and proportion word problems that link together aspects of ratio and proportion into more real life questions. This requires you to be able to take key information from a question and use your knowledge of ratios (and other areas of the curriculum) to solve the problem.

A ratio is a relationship between two or more quantities. They are usually written in the form a : b where a and b are two quantities. When problem solving with a ratio, the key facts that you need to know are:

• What is the ratio involved?
• What order are the quantities in the ratio?
• What is the total amount / what is the part of the total amount known?
• What are you trying to calculate ?

As with all problem solving, there is not one unique method to solve a problem. However, this does not mean that there aren’t similarities between different problems that you can use to help you find an answer.

The key to any problem solving is being able to draw from prior knowledge and use the correct piece of information to allow you to get to the next step and then the solution.

Let’s look at a couple of methods you can use when given certain pieces of information.

[FREE] Ratio Problem Solving Worksheet (Grade 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of ratio problem solving. 15 questions with answers to identify areas of strength and support!

When solving ratio word problems, it is very important that you are able to use ratios. This includes being able to use ratio notation.

For example, Charlie and David share some sweets in the ratio of 3 : 5. This means that for every 3 sweets Charlie gets, David receives 5 sweets.

Charlie and David share 40 sweets, how many sweets do they each get?

You use the ratio to divide 40 sweets into 8 equal parts.

40 \div 8=5

Then you multiply each part of the ratio by 5.

3\times 5:5\times 5=15 : 25

This means that Charlie will get 15 sweets and David will get 25 sweets.

There can be ratio word problems involving different operations and types of numbers.

Here are some examples of different types of ratio word problems:

Common Core State Standards

How does this relate to 6 th and 7 th grade math?

• Grade 6 – Ratios and Proportional Relationships (6.RP.A.3) Use ratio and rate reasoning to solve real-world and mathematical problems, for example, by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.
• Grade 7 – Ratio and Proportional Relationships (7.RP.A.2) Recognize and represent proportional relationships between quantities.

How to do ratio problem solving

In order to solve problems including ratios:

Identify key information within the question.

Know what you are trying to calculate.

Use prior knowledge to structure a solution.

Ratio problem solving examples

Example 1: part:part ratio.

Within a school, the total number of students who have school lunches to packed lunches is 5 : 7. If 465 students have a school lunch, how many students have a packed lunch?

Within a school, the number of students who have school lunches to packed lunches is \textbf{5 : 7} . If \textbf{465} students have a school lunch, how many students have a packed lunch?

Here you can see that the ratio is 5 : 7, where the first part of the ratio represents school lunches (S) and the second part of the ratio represents packed lunches (P).

You could write this as:

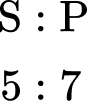
Where the letter above each part of the ratio links to the question.

You know that 465 students have school lunch.

2 Know what you are trying to calculate.

From the question, you need to calculate the number of students that have a packed lunch, so you can now write a ratio below the ratio 5 : 7 that shows that you have 465 students who have school lunches, and p students who have a packed lunch.

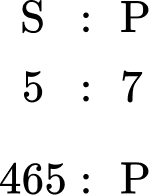
You need to find the value of p.

3 Use prior knowledge to structure a solution.

You are looking for an equivalent ratio to 5 : 7. So you need to calculate the multiplier.

You do this by dividing the known values on the same side of the ratio by each other.

465\div 5 = 93

This means to create an equivalent ratio, you can multiply both sides by 93.

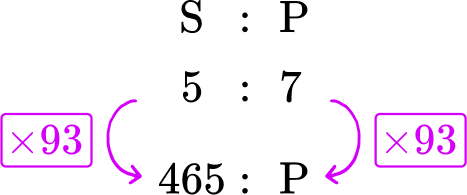
So the value of p is equal to 7 \times 93=651.

There are 651 students that have a packed lunch.

Example 2: unit conversions

The table below shows the currency conversions on one day.

Use the table above to convert £520 \; (GBP) to Euros € \; (EUR).

Use the table above to convert \bf{￡520} \textbf{ (GBP)} to Euros \textbf{€ } \textbf{(EUR)}.

The two values in the table that are important are \text{GBP} and EUR. Writing this as a ratio, you can state,

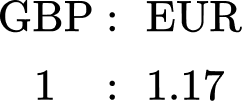
You know that you have £520.

You need to convert GBP to EUR and so you are looking for an equivalent ratio with GBP=£520 and EUR=E.

To get from 1 to 520, you multiply by 520 and so to calculate the number of Euros for £520, you need to multiply 1.17 by 520.

1.17 \times 520=608.4

So £520=€608.40.

Example 3: writing a ratio 1 : n

Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the 500 \, ml of concentrated plant food must be diluted into 2 \, l of water. Express the ratio of plant food to water, respectively, in the ratio 1 : n.

Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the \bf{500 \, ml} of concentrated plant food must be diluted into \bf{2 \, l} of water. Express the ratio of plant food to water respectively as a ratio in the form 1 : n.

Using the information in the question, you can now state the ratio of plant food to water as 500 \, ml : 2 \, l. As you can convert liters into milliliters, you could convert 2 \, l into milliliters by multiplying it by 1000.

2 \, l=2000 \, ml

So you can also express the ratio as 500 : 2000 which will help you in later steps.

You want to simplify the ratio 500 : 2000 into the form 1:n.

You need to find an equivalent ratio where the first part of the ratio is equal to 1. You can only do this by dividing both parts of the ratio by 500 (as 500 \div 500=1 ).

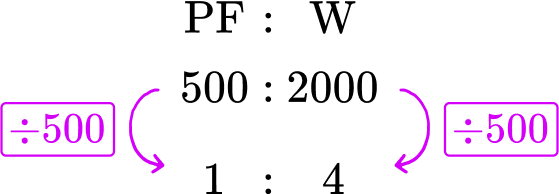
So the ratio of plant food to water in the form 1 : n is 1 : 4.

Example 4: forming and solving an equation

Three siblings, Josh, Kieran and Luke, receive an allowance each week proportional to their age. Kieran is 3 years older than Josh. Luke is twice Josh’s age. If Josh receives \$ 8 allowance, how much money do the three siblings receive in total?

Three siblings, Josh, Kieran and Luke, receive an allowance each week proportional to their ages. Kieran is \bf{3} years older than Josh. Luke is twice Josh’s age. If Luke receives \bf{\$ 8} allowance, how much money do the three siblings receive in total?

You can represent the ages of the three siblings as a ratio. Taking Josh as x years old, Kieran would therefore be x+3 years old, and Luke would be 2x years old. As a ratio, you have:

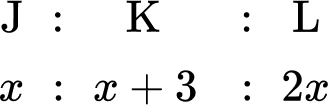
You also know that Luke receives \$ 8.

You want to calculate the total amount of allowance for the three siblings.

You need to find the value of x first. As Luke receives \$ 8, you can state the equation 2x=8 and so x=4.

Now you know the value of x, you can substitute this value into the other parts of the ratio to obtain how much money the siblings each receive.

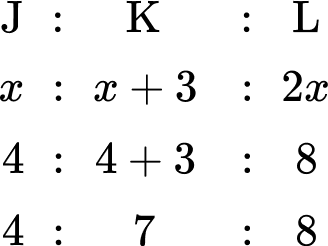
The total amount of allowance is therefore 4+7+8=\$ 19.

Example 5: simplifying ratios

Below is a bar chart showing the results for the colors of counters in a bag.

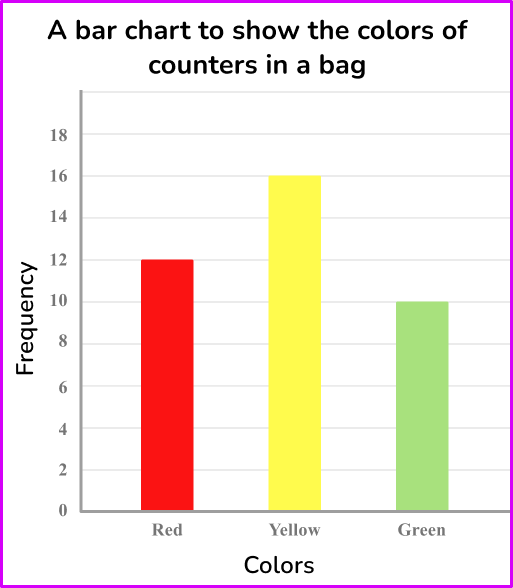
Express this data as a ratio in its simplest form.

From the bar chart, you can read the frequencies to create the ratio.

You need to simplify this ratio.

To simplify a ratio, you need to find the highest common factor of all the parts of the ratio. By listing the factors of each number, you can quickly see that the highest common factor is 2.

\begin{aligned} & 12 = 1, {\color{red}2}, 3, 4, 6, 12 \\\\ & 16 = 1, {\color{red}2}, 4, 8, 16 \\\\ & 10 = 1, {\color{red}2}, 5, 10 \end{aligned}

HCF(12,16,10) = 2

Dividing all the parts of the ratio by 2, you get

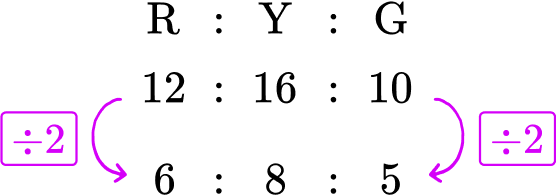
Our solution is 6 : 8 : 5.

Example 6: combining two ratios

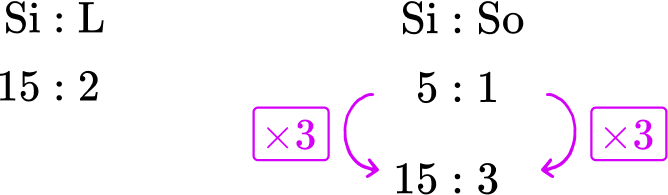
Glass is made from silica, lime and soda. The ratio of silica to lime is 15 : 2. The ratio of silica to soda is 5 : 1. State the ratio of silica:lime:soda.

Glass is made from silica, lime and soda. The ratio of silica to lime is \bf{15 : 2}. The ratio of silica to soda is \bf{5 : 1}. State the ratio of silica:lime:soda.

You know the two ratios

You are trying to find the ratio of all 3 components: silica, lime and soda.

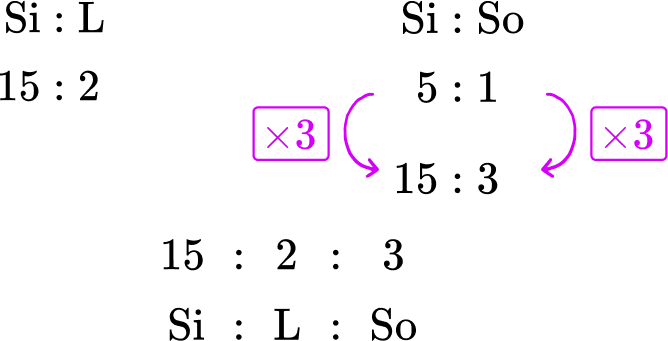
Using equivalent ratios you can say that the ratio of Silica:Soda is equivalent to 15 : 3 by multiplying the ratio by 3.

You now have the same amount of silica in both ratios and so you can now combine them to get the ratio 15 : 2 : 3.

Example 7: using bar modeling

India and Beau share some popcorn in the ratio of 5 : 2. If India has 75 \, g more popcorn than Beau, what was the original quantity?

India and Beau share some popcorn in the ratio of \bf{5 : 2} . If India has \bf{75 \, g} more popcorn than Beau, what was the original quantity?

You know that the initial ratio is 5 : 2 and that India has three more parts than Beau.

You want to find the original quantity.

Drawing a bar model of this problem, you have:

Where India has 5 equal shares, and Beau has 2 equal shares.

Each share is the same value and so if you can find out this value, you can then find the total quantity.

From the question, India’s share is 75 \, g more than Beau’s share so you can write this on the bar model.

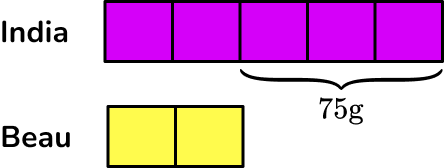
You can find the value of one share by working out 75 \div 3=25 \, g.

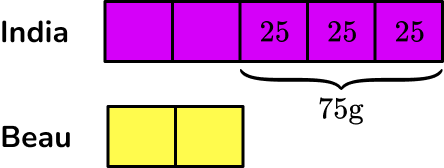
You can fill in each share to be 25 \, g.

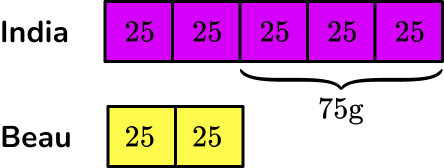
Adding up each share, you get

India=5 \times 25=125 \, g

Beau=2 \times 25=50 \, g

The total amount of popcorn was 125+50=175 \, g.

Teaching tips for ratio problem solving

• Continue to remind students that when solving ratio word problems, it’s important to identify the quantities being compared and express the ratio in its simplest form.
• Create practice problems for students using the information in your classroom. For example, ask students to find the ratio of boys to the ratio of girls using the total number of students in your classroom, then the school.
• To find more practice questions, utilize educational websites and apps instead of worksheets. Some of these may also provide tutorials for struggling students. These can also be helpful for test prep as they are more engaging for students.
• Use a variety of numbers in your ratio word problems – whole numbers, fractions, decimals, and mixed numbers – to give students a variety of practice.
• Provide students with a step-by-step process for problem solving, like the one shown above, that can be applied to every ratio word problem.

Easy mistakes to make

• Mixing units Make sure that all the units in the ratio are the same. For example, in example 6, all the units in the ratio were in milliliters. You did not mix ml and l in the ratio.
• Writing ratios in the wrong order For example, the number of dogs to cats is given as the ratio 12 : 13 but the solution is written as 13 : 12.

• Counting the number of parts in the ratio, not the total number of shares For example, the ratio 5 : 4 has 9 shares, and 2 parts. This is because the ratio contains 2 numbers but the sum of these parts (the number of shares) is 5+4=9. You need to find the value per share, so you need to use the 9 shares in your next line of working.
• Ratios of the form \bf{1 : \textbf{n}} The assumption can be incorrectly made that n must be greater than 1, but n can be any number, including a decimal.

Related ratio lessons

• Unit rate math
• Simplifying ratios
• Ratio to fraction
• How to calculate exchange rates
• Ratio to percent
• How to write a ratio
• Dividing ratios
• How to find the unit rate
• Ratio scale
• Constant of proportionality

Practice ratio problem solving questions

1. An online shop sells board games and computer games. The ratio of board games to the total number of games sold in one month is 3 : 8. What is the ratio of board games to computer games?

8-3=5 computer games sold for every 3 board games.

2. The ratio of prime numbers to non-prime numbers from 1-200 is 45 : 155. Express this as a ratio in the form 1 : n.

You need to simplify the ratio so that the first number is 1. That means you need to divide each number in the ratio by 45.

45 \div 45=1

155\div{45}=3\cfrac{4}{9}

3. During one month, the weather was recorded into 3 categories: sunshine, cloud and rain. The ratio of sunshine to cloud was 2 : 3 and the ratio of cloud to rain was 9 : 11. State the ratio that compares sunshine:cloud:rain for the month.

3 \times S : C=6 : 9

4. The angles in a triangle are written as the ratio x : 2x : 3x. Calculate the size of each angle.

You should know that the 3 angles in a triangle always equal 180^{\circ}.

\begin{aligned} & x+2 x+3 x=180 \\\\ & 6 x=180 \\\\ & x=30^{\circ} \\\\ & 2 x=60^{\circ} \\\\ & 3 x=90^{\circ} \end{aligned}

5. A clothing company has a sale on tops, dresses and shoes. \cfrac{1}{3} of sales were for tops, \cfrac{1}{5} of sales were for dresses, and the rest were for shoes. Write a ratio of tops to dresses to shoes sold in its simplest form.

\cfrac{1}{3}+\cfrac{1}{5}=\cfrac{5+3}{15}=\cfrac{8}{15}

1-\cfrac{8}{15}=\cfrac{7}{15}

6. The volume of gas is directly proportional to the temperature (in degrees Kelvin). A balloon contains 2.75 \, l of gas and has a temperature of 18^{\circ}K. What is the volume of gas if the temperature increases to 45^{\circ}K?

The given ratio in the word problem is 2. 75 \mathrm{~L}: 18^{\circ} \mathrm{K}

Divide 45 by 18 to see the relationship between the two temperatures.

45 \div 18=2.5

45 is 2.5 times greater than 18. So we multiply 2.75 by 2.5 to get the amount of gas.

2.75 \times 2.5=6.875 \mathrm{~l}

Ratio problem solving FAQs

A ratio is a comparison of two or more quantities. It shows how much one quantity is related to another.

A recipe calls for 2 cups of flour and 1 cup of sugar. What is the ratio of flour to sugar? (2 : 1)

In middle school ( 7 th grade and 8 th grade), students transition from understanding basic ratios to working with more complex and real-life applications of ratios and proportions. They gain a deeper understanding of how ratios relate to different mathematical concepts, making them more prepared for higher-level math topics in high school.

The next lessons are

• Converting fractions, decimals and percentages

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (3rd to 8th Grade)

Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.

Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!

Privacy Overview

• Number Charts
• Multiplication
• Long division
• Basic operations
• Telling time
• Place value
• Roman numerals
• Fractions & related
• Add, subtract, multiply,   and divide fractions
• Mixed numbers vs. fractions
• Equivalent fractions
• Prime factorization & factors
• Fraction Calculator
• Decimals & Percent
• Add, subtract, multiply,   and divide decimals
• Fractions to decimals
• Percents to decimals
• Percentage of a number
• Percent word problems
• Classify triangles
• Classify quadrilaterals
• Circle worksheets
• Area & perimeter of rectangles
• Area of triangles & polygons
• Coordinate grid, including   moves & reflections
• Volume & surface area
• Pre-algebra
• Square Roots
• Order of operations
• Scientific notation
• Proportions
• Ratio word problems
• Write expressions
• Evaluate expressions
• Simplify expressions
• Linear equations
• Linear inequalities
• Graphing & slope
• Equation calculator
• Equation editor
• Elementary Math Games
• Addition and subtraction
• Math facts practice
• The four operations
• Factoring and number theory
• Geometry topics
• Middle/High School
• Statistics & Graphs
• Probability
• Trigonometry
• Logic and proof
• For all levels
• Favorite math puzzles
• Favorite challenging puzzles
• Math in real world
• Problem solving & projects
• For gifted children
• Math history
• Math games and fun websites
• Interactive math tutorials
• Math help & online tutoring
• Assessment, review & test prep
• Online math curricula

Use the generator to make customized ratio worksheets. Experiment with the options to see what their effect is.

Ratios Worksheets

Equivalent Ratios

Finding the Parts from the Whole

Part to Whole

Proportions

Ratio Tables

Reducing Ratios

Representing Ratios

Scale Drawings

Writing Ratios

All About These 15 Worksheets

Introducing our comprehensive collection of ratio worksheets, designed to captivate students and deepen their understanding of essential mathematical concepts such as ratios, proportions, and their applications. These worksheets are more than just practice tools; they are structured learning experiences crafted to enhance foundational math skills that will support algebraic thinking and problem-solving later in their academic journey. Ideal for classroom use, homeschooling, or supplemental practice, these resources cater to students in upper elementary and middle school levels, providing a variety of engaging activities to strengthen their mastery of ratios, a crucial stepping stone in mathematics.

The beauty of this collection lies in its versatility and accessibility. Each worksheet is provided in an easy-to-use, downloadable PDF format, making it convenient for teachers, parents, and students to access and use them at any time. Whether they are used for quick in-class practice, targeted homework assignments, or additional review sessions, these worksheets are flexible enough to adapt to the diverse needs of learners. They also encourage independent learning, as students can work through problems at their own pace while receiving immediate feedback from the clear, step-by-step solutions provided.

One of the standout features of this collection is the incorporation of visual learning techniques, such as Bar Models. These activities ask students to draw bar diagrams to visually represent the relationship between different sets of items, making abstract concepts like ratios more concrete and understandable. For instance, students might be asked to solve a problem like, “The ratio of red balls to blue balls is 3:2. If there are 12 red balls, how many blue balls are there?” Through the bar model, students can break down the problem, step by step, and visualize the proportional relationships at play. This not only builds their confidence in solving ratio problems but also caters to learners who thrive with visual aids.

Another key component of this collection is the Ratio Tables worksheet, where students practice completing tables to find equivalent ratios. By filling in missing values and scaling ratios up or down, students hone their skills in proportional reasoning-a skill that is critical for tackling more advanced math problems like those found in algebra and geometry. These worksheets go beyond simple rote learning; they challenge students to think critically about how numbers relate to each other, preparing them to solve real-world problems such as calculating unit rates (e.g., cost per item) or determining rates of change (e.g., speed per hour). Through engaging and thought-provoking exercises, these worksheets aim to build a solid foundation that will support students throughout their mathematical education and beyond.

Here are all the different types of ratio worksheets that we have available for you:

These are visual tools that use rectangular bars to represent numerical relationships, helping students break down and solve word problems. They develop skills in addition, subtraction, multiplication, division, and understanding fractions, ratios, and algebraic concepts.

These worksheets help students practice finding and comparing ratios that have the same value by using multiplication or division. They focus on building proportional reasoning skills, essential for understanding fractions, scaling, and solving real-world problems involving ratios.

Finding The Parts From The Whole

These worksheets guide students in calculating individual parts when given the total, often using fractions, percentages, or ratios. They help develop skills in proportional reasoning, division, and fraction-to-decimal conversions, crucial for solving problems involving portions of a whole.

Part To Whole Ratio

These worksheets focus on comparing a part to the whole using ratios, helping students understand the relationship between individual quantities and their total. They develop skills in ratio comprehension, proportional reasoning, and connecting ratios to fractions and percentages.

These worksheets help students solve problems where two ratios are set equal to each other, reinforcing the concept of equivalent ratios. They focus on developing skills in cross-multiplication, scaling, and applying proportional reasoning to real-world contexts.

These worksheets use tables to organize and compare equivalent ratios, helping students see patterns in proportional relationships. They build skills in multiplication, division, and scaling, essential for understanding ratios and solving proportion problems.

Reducing Ratios To The Lowest Terms

These worksheets teach students how to simplify ratios by dividing both terms by their greatest common factor. They develop skills in finding common factors, simplifying numerical expressions, and understanding the concept of equivalent ratios.

These worksheets involve interpreting and creating drawings where objects are represented proportionally to their actual size using a specific scale. They enhance skills in scaling, measurement, ratio reasoning, and applying proportions to real-life scenarios like maps and architectural plans.

These worksheets focus on calculating the rate for a single unit, helping students understand how to compare quantities like speed, cost, or density. They strengthen skills in division, proportional reasoning, and applying rates to solve practical problems.

Using Shapes And Objects To Represent The Ratio

These worksheets use shapes and objects to visually represent ratios, allowing students to see the relationships between quantities. They develop spatial reasoning, proportional thinking, and the ability to translate visual models into numerical ratios.

These worksheets teach students how to express relationships between quantities in ratio form, using both words and numbers. They develop skills in identifying part-to-part and part-to-whole relationships, as well as simplifying and interpreting ratios in various contexts.

Ratios vs. Proportions

Ratio and proportion are fundamental mathematical concepts used to express relationships between numbers, quantities, or measures. Both of these terms are often used interchangeably in everyday language, but in mathematics, they have distinct meanings and applications. Understanding their similarities and differences is essential for solving problems related to scaling, comparison, and equivalence.

Similarities

At their core, both ratio and proportion involve comparisons between quantities. A ratio is a comparison between two quantities, while a proportion refers to the equivalence of two ratios. Thus, a proportion is essentially a relationship between two ratios, meaning they share a common foundation in the idea of comparison.

Relationship with Numbers – Both ratios and proportions deal with relationships between numbers, focusing on how one number relates to another in terms of size or quantity. For instance, in the ratio a:b, the comparison between a and b mirrors the concept in a proportion, where a:b=c:d.

Multiplicative Nature – Ratios and proportions are both multiplicative. In a ratio, you can scale both terms (e.g., doubling or halving both numbers in the ratio) without changing the fundamental relationship between the numbers. Similarly, proportions rely on this scaling, as two ratios are said to be proportional if they can be transformed into one another by multiplication or division by the same number.

Applications in Real-Life Situations – Both concepts are widely applied in fields such as physics, economics, engineering, and even art. Ratios are used to compare quantities such as speeds, densities, or financial performance, while proportions are key to maintaining the balance of those ratios, like ensuring consistent scaling in a recipe or model.

Differences

While ratio and proportion are related, they are distinct in terms of their definitions, usage, and mathematical properties. A ratio is simply a way of comparing two numbers. It expresses how much of one quantity exists compared to another. For instance, the ratio of 3 apples to 2 oranges can be written as 3:2 or 3/2. In contrast, a proportion is an equation that shows two ratios are equal. For example, if the ratio of boys to girls in one class is the same as the ratio in another class, it can be written as 3/2 = 6/4, indicating that the two ratios form a proportion.

In terms of function, a ratio is used for direct comparison. It highlights how two quantities relate to each other in a single instance, such as comparing measurements or combining items in a mixture. A proportion, however, goes further by determining whether two ratios are equivalent. This makes proportions useful for solving problems involving scaling or finding unknown values. For example, if two equivalent ratios form a proportion, you can solve for a missing value by maintaining their equality.

Ratios are typically represented using a colon or a fraction, such as a:b or a/b. While they indicate a relationship, ratios alone do not signify equality between quantities. Proportions, on the other hand, are represented by equations where two ratios are set equal to each other, such as a:b = c:d or a/b = c/d. This notation specifically denotes that the two compared ratios are equal.

When solving problems with ratios, you might simplify, compare, or apply them in practical contexts, like scaling quantities. Proportions, however, often involve solving for an unknown value. Given three terms of a proportion, you can use cross-multiplication to find the fourth. For instance, in the proportion a/b = c/d, cross-multiplying gives a x d = b x c, which helps solve for unknowns in proportional relationships.

Mathematically, the interpretation of ratios and proportions differs as well. A ratio represents a single, fixed relationship, such as 3/2, emphasizing the comparison between two quantities without implying equality. A proportion, on the other hand, involves two ratios set equal to each other, indicating a constant rate of change between the quantities being compared. For instance, in the proportion a/b = c/d, an increase in a results in a proportional increase in c, preserving the equality between the two ratios.

• Skip to primary navigation
• Skip to main content
• Skip to primary sidebar

Teaching Expertise

• Classroom Ideas
• Teacher’s Life
• Deals & Shopping
• Privacy Policy

Ratio And Proportion Activities For Middle School: Task Cards, Worksheets, Manipulatives, And Other Resources

January 15, 2024 //  by  Lesa M.K. Bullins, EdS

Ratio and proportion can be quite difficult math concepts to comprehend; therefore, it is of particular importance that students are engaged in interesting learning activities for these complicated concepts.

Middle school students need to build on important basic mathematical structures to develop competence in the complex concepts of ratio and proportion. Scroll down and enjoy this top 20 list of fun ratio and proportion activities for your middle school classroom!

1. It’s Goldfish!

Break out the food and get middle schoolers engaged through snacking! Students can use goldfish and other easy-to-snack foods to be able to develop a realistic, hands-on understanding. Check the lesson “something is fishy” to learn more about how to use this yummy snack to get your middle schoolers excited about math!

Learn More: Cognitive Cardio Math

2. Shifting Stations

Shift the worksheets out and the task card stations in! Get students moving about the room while they practice instead of just sitting at their desks by preparing task cards with ratio and proportions activities and questions!

Learn More: My Math Resources

3. Paper Planes

All kids love to make paper planes, so instead of banning those things from your classroom, embrace them! Let students make the paper planes, then use ratio and proportion to calculate and compare data! There are many ways this can be adapted to teach whatever level of concepts your students are learning (so it’s great for differentiation and building core skills) in relation to ratios and proportions!

Learn More: Tiarra’s Teaching Techniques

4. Rev up the Worksheets

Make boring worksheets a little more entertaining by adding a little extra like a puzzle to solve, matching actions, secret messages, etc. This is an easy way to make existing worksheets a little more of a fun ratio and proportion activity. This is also a good activity for subs as it is easy for them to give students to practice and strengthen concepts they have already learned.

5. Make it Realistic

You can use real-life scenarios that are relatable to student interests, so students can better see how ratio and proportion help them solve realistic, applicable problems! Link in technology for an added connection like this great lesson activity from PBS Kids.

Learn More: PBS Learning Media

6. Sweet Treat Holidays

Break out the candy with fun holiday-themed practice like this Halloween M&M ratio activity. You can adapt this to include other cultural holidays, obscure celebration days, etc. to make it applicable to any time of year as well as the added bonus of creating inclusive classroom culture and engaging all students.

Learn More: Kelly McCown

7. Manipulatives

A small change to make worksheets more interactive is the addition of math manipulatives. If you do not want to jack up the students on sweets every time you get interactive, then replace those candies with small fidgets or pre-made math manipulatives.

Activity sheets with the manipulatives are much more lively than a boring activity of asking and answering questions.

Learn More: Middle School Math Rules

8. Create Competition

Everyone likes to win! Students love competition, so bring that spirit to math by creating races. Make sure to make winning with correct answers the most lucrative, but also make the act of finishing lucrative, so you do not create a system that demotivates!

Learn More: Math Snippets

9. Show Off

Even older students like to show off and be proud of their work, so creating unique ways to display student work can have tons of added impact on classroom culture and positive effects on student learning.

Have students create posters, pennants, and other activities that solve ratio and proportion problems. These additional activities can be used in a variety of ways, like an art activity, a morning activity per day, or exit tickets!

Most importantly, this activity in class will create a classroom that builds a growth mindset by displaying student work and allowing students to create their own anchor charts.

Learn More: Scaffolded Math

10. Truth or Dare

Embrace the daring side of students by creating a truth-or-dare game. There are a lot of ways to make this concept work like making the “dare” being solving challenging questions to get the correct answer and “truth” being the recall of related concepts like vocabulary or solving more basic math building blocks related to ratios and proportions.

This will allow students to differentiate depending on their comfort with the subject, thus they can build skills up from where they are.

11. Engage Other Subjects

Let students use maps and geographical data to see the connection between math and the world around them, thus easily engaging social studies and social sciences. You can see some scale ratio examples in this video to spur your creativity about applying this idea to your math classroom activities.

Learn More: YouTube

12. Have an Amazing Race

This Amazing Race scavenger hunt activity is a delightful way to facilitate collaborative learning in your classroom. Add a twist to this iconic game by incorporating various ratio and proportion problems that your kiddos will have to solve before you provide them with the clues they’ll need to race to the finish line.

13. Engage in Examples Online

Give students a technology-based online opportunity to practice by doing standards-based examples. This is a great way to help students apply the concepts and ensure they are meeting the various standards on ratios and proportions.

Learn More: Illustrative Mathematics

14. Tic Tac Toe

Break out the fun method of understanding proportions with the tic tac toe method by James Sullivan! Students will enjoy learning proportion concepts with this interesting method!

15. Online Games

Let students practice ratio and proportion concepts with fun online games. Students can explore the Dirt Bike Proportions Game and others are found on Hoodamath!

Ratio Rumble and Bad Date are just a couple of the fun math games for ratios that are found here on Math Snacks!

Students will have a blast getting to play and learn with these review games!

Learn More: Hoodamath and Math Snacks

16.  Throw a Party

You can create a party around a certain cultural holiday or accomplishment. You can even find some fun obscure celebrations to create a party around. Just like with the themed activities from number six, this type of activity for ratio and proportions can build classroom culture as well as math skills. Students will use the party planning process to practice ratios and proportions such as portions per person.

17. Make Music

Let students explain their understanding through music. Students can work in groups to make ratios and proportions parody songs. This collaborative approach engages interest and self-expression! Check out inspiration by listening to this ratios parody using the Moana song How Far I’ll Go on the Songs for School YouTube channel.

18. Get Animated

Engage technology further in the classroom by letting students express their understanding through creating an animation. Students could work in groups and use some simple online programs like Powtoon, Doodly, or Pixteller to create short animations that solve a realistic example question using ratio and proportion!

Students will be thrilled at this creative way to express proportional relationships and ratio relationships.

19. 4-in-a-Row Ratio

Let your young minds practice in pairs using this wonderful game that will allow them to link visuals with ratio concepts. To play this game, you’ll encourage them to place counters on shape mats according to a displayed ratio. It’s a great activity if you’re looking to reinforce the concept of ratios, but it also takes a bit of strategy and quick thinking because to win this game your students will need to place four of their counters in a row.

20. Bullseye

Continuing with another fun idea from the TeacherACER YouTube channel, students can also have a bullseye race with magnetic bullseyes and magnetic darts. Students will answer ratio and proportion questions after hitting a target racing through the targets and questions!

What a great way to develop essential understandings without worksheets! Check out how to do it at the minute forty-five mark of the video.

• Skills by Standard
• Skills by Grade
• Skills by Category

Go to profile

• Assignments
• Assessments
• Report Cards
• Our Teachers

Common Core - State Standards Initiative

Understanding ratios is crucial for solving problems relating to proportions and percents. Math Games makes reviewing this higher-level math skill a breeze, with our suite of enjoyable educational games that students won’t want to stop playing!

Our free resources include mobile-compatible game apps, PDF worksheets, an online textbook and more. Students can use these tools to blend study with play as they practice:

• Describing pictures as ratios
• Calculating percents and prices
• Comparing ratios
• Solving proportions
• Finding the slope of a graph

Help the kids in your life look forward to reviewing math! Our games are tailored to a variety of grade levels and become easier or more challenging depending on how well users are playing. Select one of the skills listed above to check them out!

• WordPress.org
• Documentation
• Learn WordPress
• Members Newsfeed

20 Fun Ratio and Proportion Activities for Middle School

• Math Education

Introduction:

Instilling a strong understanding of mathematical concepts, such as ratio and proportion, is essential for middle school students. By providing fun and engaging activities, educators can make learning enjoyable and increase comprehension. Here are 20 exciting ratio and proportion activities designed specifically for middle school students.

1.Skittle Counting:

Give each student a small bag of Skittles. Have them sort the colors and create ratios comparing the number of each color to the total amount.

2.Paint Mixing:

Supply students with three primary colors — red, blue, and yellow — then have them create different shades by following assigned ratios.

3.Cooking with Ratios:

Using simple recipes, such as making lemonade or cookies, teach students about using ratios in cooking.

4.Map Scaling:

Have students create scale models of their school or neighborhood using given scaling ratios.

5.Currency Conversion:

Provide currency exchange rates and have students calculate how much money they would receive when converting their money into another currency.

6.Candy Bar Fractions:

Using various candy bars with different proportions represented in their packaging design, have students compare the different fractions.

7.Proportion Pictionary:

Have students draw objects in proportionate sizes according to specific calculations.

8.Building Budgets:

Set up a pretend store filled with items at different prices and provide an imaginary budget. Students must determine the proportions they can buy within their allocated budget.

9.Solve Proportion Problems:

Create a list of word problems involving real-world scenarios that require solving for ratio or proportion.

10.Grocery Store Trip:

Take your class to a grocery store or set up a pretend store inside your classroom where students will use ratios to calculate discounts on items during sales events.

11: Newspaper Ads Analysis:

Ask students to analyze ads in newspapers and evaluate the claims made based on proportions or percentages given in the ad copy.

12.Speed and Distance Calculation:

Using ratios, have students calculate how long a road trip would take given different average speeds and distances.

13.Ratio Hunt:

Arrange objects in predetermined ratios throughout the classroom and have students hunt for the specific object combinations.

14.Sports Statistics Comparison:

Give students sports statistics of their favorite players or teams and ask them to compare the performance ratios.

15.Proportional Art:

Incorporate proportions into art projects to teach size comparisons between drawn or painted objects.

16.Recipe Resizing:

Have students adjust the ingredient quantities in a given recipe to serve different numbers of people while maintaining proper proportions of each ingredient.

17.Sharing Meal Portions:

Provide a meal scenario with various items to share amongst friends, teaching students how to evenly portion food according to given ratios.

18.Classroom Decorating Decisions:

Give your class a predetermined budget for purchasing classroom decorations, allowing them to use ratio calculations in their decision-making about which decorations provide better value.

19: Water Conservation Game:

Students simulate daily activities that use water, such as brushing teeth or taking a shower, illustrating how using water in different amounts affects total consumption with different proportions.

20.National Park Ecosystem Study:

Discuss and calculate the relationships between different species’ populations in a particular national park ecosystem using scientific data collected by researchers.

Conclusion:

These 20 fun and engaging activities will help middle school students better understand and enjoy learning about ratio and proportion concepts. By incorporating hands-on experiences and connecting mathematics to the real world, educators can provide meaningful learning experiences that reinforce critical skills.

Related Articles

Connecting mathematics to fun and practical applications can make it a favorite…

Mathematics forms an integral part of educational curriculums around the world, establishing…

Composite numbers are integers that have more than two distinct positive divisors.…

Pedagogue is a social media network where educators can learn and grow. It's a safe space where they can share advice, strategies, tools, hacks, resources, etc., and work together to improve their teaching skills and the academic performance of the students in their charge.

If you want to collaborate with educators from around the globe, facilitate remote learning, etc., sign up for a free account today and start making connections.

Pedagogue is Free Now, and Free Forever!

• New? Start Here
• Frequently Asked Questions
• Privacy Policy
• Terms of Service

Are you sure you want to delete post?

This post cannot be restored anymore.

• Registration

Don't you have an account? Register Now! it's really simple and you can start enjoying all the benefits!

We just sent you an Email. Please Open it up to activate your account.

I allow this website to collect and store submitted data.

Browse by Topics

• Kids Learning & Activities
• Basic Language Skills
• Numbers and Operation
• Measurement
• Data Handling
• KIds Learning & Activities
• Basic Language Sills
• Numbers and Operations

RATIO WORKSHEETS

Welcome to our collection of ratio worksheets designed to help students practice and master the concept of ratios. Ratios are fundamental in mathematics and are used to compare quantities in different situations. Whether you’re introducing ratios for the first time or reinforcing previously learned concepts, these worksheets offer a variety of exercises suitable for different levels of proficiency. From basic ratio problems to more complex scenarios, students will find ample opportunities to sharpen their skills and deepen their understanding of ratios.

Our worksheets are designed to gradually increase in difficulty, allowing students to build upon their skills and knowledge as they progress through the exercises.

Ratio Worksheets

Parts of a ratio.

Write the parts of ratio using the given pictures.

Parts of a Ratio #1

Parts of a ratio #2, parts of a ratio #3, finding ratio.

Find the ratio and answer the given word problems.

Finding Ratio #1

Finding ratio #2, finding ratio #3, ratio in three ways.

Write the ratio in three different ways.

Ratio in Three Ways #1

Ratio in three ways #2, ratio in three ways #3, color & draw.

Color the pictures for the given ratio. Draw the pictures for the given ratio.

Color & Draw #1

Color & draw #2, color & draw #3, shaded/unshaded region.

Find the ratio for the shaded and unshaded regions.

Shaded/Unshaded Region #1

Shaded/unshaded region #2, shaded/unshaded region #3, simplifying ratio.

Simplify the ratio and color the way from start to finish.

Simplifying Ratio #1

Simplifying ratio #2, simplifying ratio #3, equivalent ratio.

These worksheets describe the equivalent ratio for easy understanding.

Equivalent Ratio #1

Equivalent ratio #2, equivalent ratio #3, ratio: money.

Here money concepts included, to find the ratio of shares.

Ratio: Money #1

Ratio: money #2, ratio: money #3, using customary units.

These ratio worksheets have problems with the customary units.

Using Customary Units #1

Using customary units #2, using metric units.

These ratio worksheets have problems with the metric units.

Using Metric Units #1

Using metric units #2, using metric units #3, ratio word problems.

Our worksheets help students understand how ratios are used in everyday situations, making learning more relatable and engaging.

Ratio Word Problems #1

Ratio word problems #2, ratio word problems #3, get posts by email.

Subscribe now and get regular updates & offers immediately

Stay connected with us:

• Alphabet Learning
• Color Letters
• Cursive Writing
• Colorful Charts
• Number Charts
• Number Names
• Addition Activity
• Picture Addition
• Addition Tables
• Subtraction Activity
• Picture Subtraction
• Multiplication Tables
• Days, Months & Seasons
• Reading Comprehension
• Horizontal Addition
• Horizontal Subtraction
• Vertical Subtraction
• Multiplication Activity
• Picture Multiplication
• Odd or Even Numbers
• Horizontal Multiplication
• Subtraction Ending With Zero
• Addition with Three Rows
• Division Tables
• Division Activity
• Tally Worksheets

Copyright © 2024. Free Math Worksheets. All reserved!